拉格朗日插值方法

Posted 2023-03-16

参考技术A

对于函数y=f(x), 在n+1个相异点 上的函数值为 要求一个次数不超过 n 的多项式
使得，
在结点 上有

这时候称 为插值多项式

显然 的 n+1 个系数满足

记方程的系数矩阵为A

显然是一个范德蒙行列式，且只需要 互不相同，则方程组必有解。

还需要考虑一个截断误差

拉格朗日插值多项式
首先构造一个基函数

且这个函数满足条件

于是拉格朗日插值方法就得到了。

当
利用roller定理推导出，对于任意的x属于[a, b]
插值多项式的余项

如题：

由拉格朗日插值法

拉格朗日插值法

拉格朗日(Lagrange)插值C++

声明：仅为个人笔记，相关内容仅供参考。

---

目录

• 拉格朗日(Lagrange)插值C++
• 一、拉格朗日插值
• 二、误差分析:
• 三、代码实现:

---

一、拉格朗日插值

Lagrange插值属 n 次多项式插值，其成功之处在于用构造插值基函数的方法解决了求 n 次多项式插值函数的问题。

在实际应用中的函数y=f(x)有可能出现这样的问题：函数没有解析表达式，只有一系列离散的测量点组成的表格。如下表格：

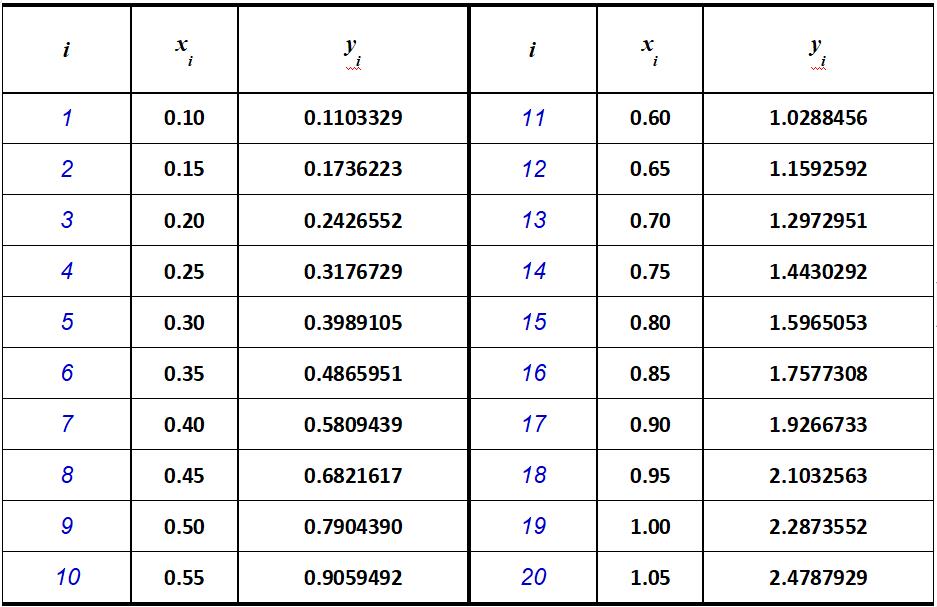
这里直接引出n次拉格朗日插值：

二、误差分析:

不难发现 ：理论上，随着节点数n的增加，Lagrange插值就越精确。
为什么说理论上呢，因为在实际操作中肯定是不一样的。计算机中用有限位的浮点数存储数据导致储存值与真实值存在误差，这便是舍入误差。随着随着节点数n增加，运算次数显著增加，舍入误差积累变大。因此节点数n达到一定值后，增加反而对导致误差越开越大，甚至会超过我们预期。一般我们在计算插值时所选节点数不超过8个。

三、代码实现:

大致思路：

1. 用户输入：输入或事先存储表格数据，输入待求插值点t和节点数m(m-1次插值)
2. .选取节点：根据所需节点数和表格数据判断节点起始位置和末位置
3. 计算插值：根据所选节点和待求插值点t计算Lagrange插值
4. 结果输出：返回插值并输出

这里啰嗦多两句(针对萌新讲的，自行选择跳过)预先解释一下代码思路：

• 节点数选取：①首先判断输入节点数是否合法：可能存在节点数超过所测得点个数；可能存在节点数小于2；②起始位置和末止位置的节点可能超越测得点的首位置和末位置，即带求插值点t靠前(或靠后)导致向前(或向后)取节点时越界。解决方法：此时我们在不改变m-1次插值的前提下，可以将测得值数据首(末)位作为起始(末止)位置，那么节点的末止(起始)位置依次推移。③如果前面情况都避开了，那么这才是进入了一个正常状态。遍历找到i满足：代求插值点在Xi之后。那么起始位置为：i-m/2;末止位置为:①m为奇数时:i+m/2;②m为偶数时: i+m/2-1;这里再再啰嗦两句,判断的i已经在t后面,那么如果节点数m为偶数，那么起始位置就向前移动m/2，模式位置因为有了i的存在就少一个，即向后移动m/2-1就行；那么m为奇数情况，以i为中心向前、后各数m/2个数作为始末节点就行。注：int型的奇数除以二后得到的数为去尾的整数，如：取3个点，m/2=1,三个点为i-1，i,i+1。
• 核心步骤:其实这部很简单，对应n-1次Lagrange插值表达式可以看到：n项式每一项为分子分母都是n-1个因式并乘上一个fx值，分母减数x不同于被减数的x,并且被减数x对应的f(x)就是乘上的fx值，分母和分子减数相同。那么循环两层计算就可以得到结果，第一层循环为：n个节点数得到的n-1项次求和计算；第二层循环为：n个节点得到的每一项对应分母的n-1次的乘法，分子的n次乘法(算上一次与fx的)。

#include<iostream>
using namespace std;
double Lagrange(double x[],double f[],double t,const int n,int m=8){
	if (n < m) {
		cout << "节点数过多或者数据不足！" << endl;
		return -1;
	}
	//选取节点
	int start, end;
	for (int i = 0; i < n; i++) {
		if (x[i] > t) {
			if (i - m / 2 < 0) {
				start = 0;
				end = m-1;
				break;
			}
			else start = i - m / 2;
			if ((i + m / 2 - (m - 1) % 2) > n - 1) {
				start = n - m ;
				end = n - 1;
				break;
			}
			else end = i + m / 2 - (m - 1) % 2;
			break;
		}
	}
	//核心步骤:累加计算含有f(Xi)对应的项的值
	double sum = 0, temp;
	for (int i = start; i <= end; i++) {
		 temp =  f[i];
		for (int j = start; j <= end; j++) {
			if (i != j) temp *= ((t - x[j]) / (x[i] - x[j]));
		}
		sum += temp;
}
	return sum;
}
int main(){
	//样表数据
	double x[] = {0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50,0.55,
	              0.60,0.65,0.70,0.75,0.80,0.85,0.90,0.95,1.00,1.05};
	double f[] = { 0.1103329,0.1736223,0.2426552,0.3176729,0.3989105,
				   0.4865951,0.5809439,0.6821617,0.7904390,0.9059492,
				   1.0288456,1.1592592,1.2972951,1.4430292,1.5965053,
				   1.7577308,1.9266733,2.1032563,2.2873552,2.4787929};
	double t;
	cout << "请输入带求点X值：" << endl;
	cin >> t;
	//执行该点的1-7次插值
	for (int i = 2; i <= 8; i++)
		cout <<"该点的" << i - 1 << "次拉格朗日插值为：" << Lagrange(x, f, t, 20, i) << endl;
	system("pause");
	return 0;
}