浅谈算法——拉格朗日插值

Posted 2021-11-23 wolfycz

拉格朗日插值法：是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法（摘自某度百科）

首先我们需要知道，拉格朗日插值法有何用？

---

举例子永远是最好的方法

比如说，已知下面这几个点，我想找到一根穿过它们的曲线：

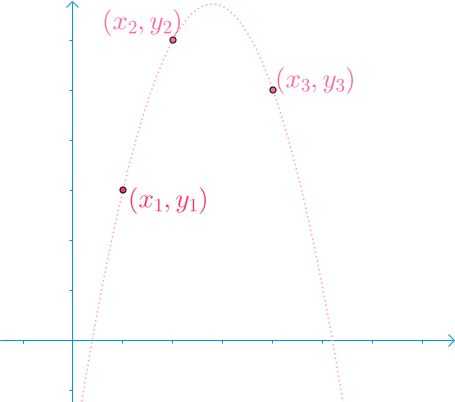
\\(k+1\\)个点是肯定可以确定一个\\(k\\)次函数的，因为待定系数法啊，然后我们假设函数为\\(f(x)=a_0+a_1x+a_2x^2\\)，然后我们就有
\\[ \\begin{cases}y_1=a_0+a_1x_1+a_2x_1^2\\nonumber\\\\y_2=a_0+a_1x_2+a_2x_2^2\\nonumber\\\\y_3=a_0+a_1x_3+a_2x_3^2\\nonumber\\end{cases} \\]
可是可以，但是扩展性不强……毕竟考场上没有可以解多元一次方程的机子……手动推通解的话……呵呵

拉格朗日也是这样想的，但是他觉得：我可以通过三根二次曲线相加得到这个函数，那么是怎样的三根曲线嘞？

第一根曲线\\(f_1(x)\\)，满足\\(f_1(x_1)=1,f_1(x_2)=f_1(x_3)=0\\)

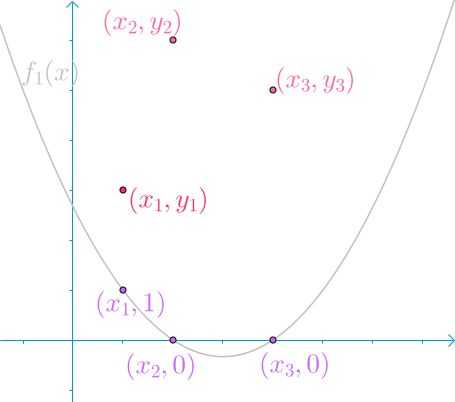
然后第二、三根曲线类似

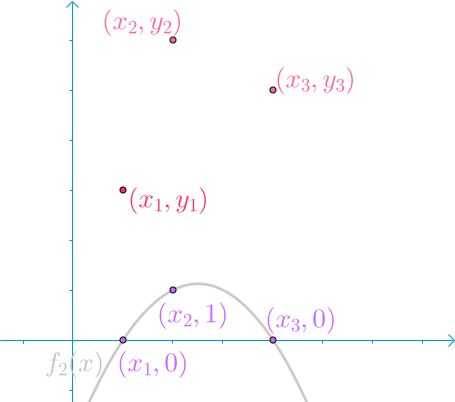
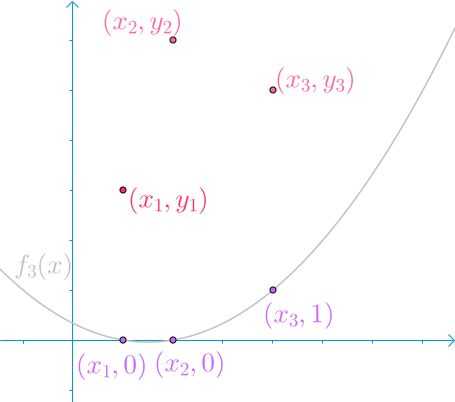
我们可以发现

• \\(y_1f_1(x)\\)可以保证，在\\(x_1\\)处，取值为\\(y_1\\)，其余两点取值为0
• \\(y_2f_2(x)\\)可以保证，在\\(x_2\\)处，取值为\\(y_2\\)，其余两点取值为0
• \\(y_3f_3(x)\\)可以保证，在\\(x_3\\)处，取值为\\(y_3\\)，其余两点取值为0

那么
\\[ f(x)=y_1f_1(x)+y_2f_2(x)+y_3f_3(x) \\]
可以一一穿过这三个点

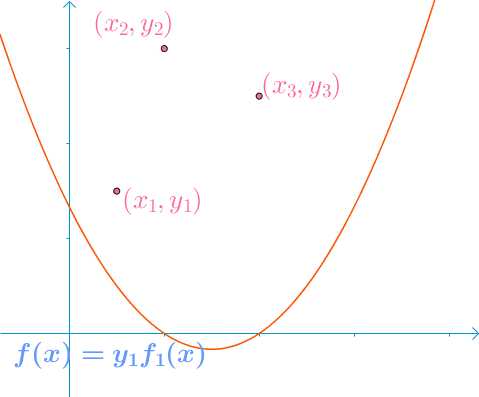
当函数不是二次，而是多次的时候，这个方法同样成立

于是前人根据这个方法，总结出了拉格朗日插值法的一般式，即
\\[ f(x)=\\sum\\limits_{i=0}^ky_i\\prod\\limits_{j\\not =i}\\dfrac{x-x_j}{x_i-x_j} \\]
(因为1～k+1写起来很丑，所以这里写的是0～k，本质相同)

我们可以发现，任意代入一个\\(x_k\\)，都必然有\\(f(x_k)=y_k\\)，过程留给读者自己推导

这样我们就可以在\\(O(k^2)\\)的时间内求出\\(f(x)\\)

---

我们再来考虑一些特殊的情况，比如\\(x_i\\)连续的情况

我们先把式子抄一遍
\\[ f(x)=\\sum\\limits_{i=0}^ny_i\\prod\\limits_{j\\not =i}\\dfrac{x-x_j}{x_i-x_j} \\]
由于\\(x_i\\)连续，所以我们可以把分子用前后缀积来表示
\\[ P_i=\\prod\\limits_{j=0}^i(x-x_j),S_i=\\prod\\limits_{j=i}^n(x-x_j) \\]
然后分母可以写成阶乘的形式，式子变成
\\[ f(x)=\\sum\\limits_{i=0}^ny_i\\dfrac{P_{i-1}·S_{i+1}}{(-1)^{n-i}i!(n-i)!} \\]
那么我们就可以在\\(O(k)\\)的时间内算出\\(f(x)\\)的值了

---

至于一些应用，最常见的就是求\\(\\sum\\limits_{i=1}^ni^k\\)的值，也就是求幂和，根据这里的式子可以得到
\\[ S_k(n)=\\sum\\limits_{i=1}^ni^k=\\dfrac{(n+1)^{k+1}-\\sum\\limits_{j=0}^{k-1}\\binom{k+1}{j}S_j(n)-1}{k+1} \\]
容易发现其为\\(k+1\\)次多项式，于是我们可以使用拉格朗日插值法

其中\\(i\\in[0,k+1]\\)的取值我们用线筛，对于每个素数我们暴力快速幂，这部分时间复杂度为\\(O(\\dfrac{k}{\\ln k}·\\log k)=O(k)\\)

所以总时间复杂度为\\(O(k)\\)