拉格朗日插值法

Posted 2022-09-16 live4m

拉格朗日插值法:

拉格朗日插值法是一种多项式插值方法。
给定n+1个坐标不同的点，拉格朗日插值法可以给出一个恰好经过这n+1个点的多项式函数。

有一类题是给出n+1个点，要求输出这n+1个点构成的多项式在某一其他位置的取值。
一种做法是高斯消元计算出多项式的系数，然后带入求值，复杂度为O(n³)。
而拉格朗日插值法可以在复杂度O(n²)解决问题。

拉格朗日基本多项式（插值基函数）:

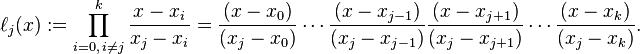
拉格朗日插值多项式:

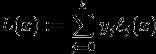
这个多项式恰好经过给定的n+1个点。
验证：对于给定的n+1个点中的任意x，代入拉格朗日基本多项式可以发现，当且仅当x=j的时候l(x)=1，其他情况下l(x)都为0，因此L(x)=y对于给定的n+1个点都成立。

优化:

当x连续时候，例如x取值为0-n，则：

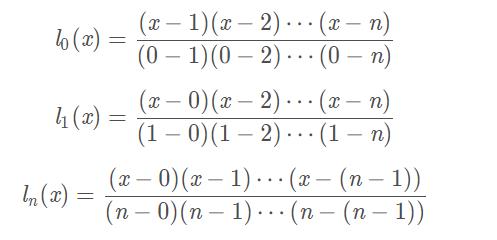
分子：只需要预处理p=(x−0)(x−1)(x−2)⋯(x−n)，求某一项li的分子计算p/(x-i)即可(取模意义下把除法变为乘逆元)。
或者计算前缀积pre和后缀积suf，求li的分子计算pre(i-1)*suf(i+1)即可。
分母：观察发现li的分母为：i!(−1)^n-i(n−i)!，预处理阶乘逆元+判断正负即可。

优化之后复杂度降为了O(n)

缺点：

插值点的数量变化，基本多项式就会变化，必须O(n²)重新计算，这时可用重心拉格朗日插值法或牛顿插值法代替。

---

重心拉格朗日插值法：

待补充

---

参考：

https://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html
https://www.cnblogs.com/zwfymqz/p/10063039.html
https://blog.csdn.net/ftx456789/article/details/90750508

---

P4781 拉格朗日插值

题意：

给定这n个点，请你确定这个多项式，并求出f(k)998244353的值。

思路：

只有一组数据，拉格朗日插值法直接算就行了，复杂度O(n²)

code：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxm=2e3+5;
const int mod=998244353;
int x[maxm],y[maxm];
int ppow(int a,int b,int mod)
    a%=mod;
    int ans=1;
    while(b)
        if(b&1)ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    
    return ans;

int Lagrange(int n,int *x,int *y,int k)//求n次多项式f(k)的值
    int ans=0;
    for(int i=0;i<=n;i++)
        int up=1,down=1;
        for(int j=0;j<=n;j++)
            if(i!=j)
                up*=(k-x[j]);
                up%=mod;
                down*=(x[i]-x[j]);
                down%=mod;
            
        
        ans+=y[i]*up%mod*ppow(down,mod-2,mod)%mod;
        ans%=mod;
    
    return (ans+mod)%mod;

signed main()
    int n,k;
    cin>>n>>k;
    n--;//n个点确定n-1次多项式
    for(int i=0;i<=n;i++)
        cin>>x[i]>>y[i];
    
    cout<<Lagrange(n,x,y,k)<<endl;
    return 0;

---

2019 ICPC南昌邀请赛 B.Polynomial

题面：

题意：

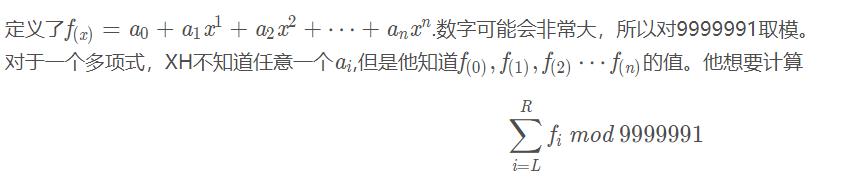
思路:

因为给定取值为0-n，是连续的，所以可以O(n)插值
题目所求容易想到前缀和，但L和R范围为1-9999990，f(n)每一项计算都是O(n)的，把前缀全部计算出来显然行不通

这里要知道一个知识：n次多项式的前缀和是n+1次多项式，设S(x)为f(i)的前缀和，则S(x)是一个n+1次多项式。
先用拉格朗日插值法计算出f(n+1)，再计算出f(0)-f(n+1)的前缀和S(0)-S(n+1)，一共n+2项，而且取值也是连续的。
利用这n+2项配合拉格朗日插值法即可计算出任意S(x)，答案就是S(R )-S(L )

ps：
用int的话，每个乘法之前要记得转化成longlong，防止乘法结果爆int。

code:

//https://nanti.jisuanke.com/t/40254
#include<bits/stdc++.h>
using namespace std;
const int maxm=1e3+5;
const int mod=9999991;
int inv[mod+5];
int finv[maxm];
int a[maxm];
void init()//预处理普通逆元和阶乘逆元
    inv[1]=1;
    for(int i=2;i<mod+5;i++)
        inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod;
    
    finv[0]=1;
    for(int i=1;i<maxm;i++)
        finv[i]=1LL*finv[i-1]*inv[i]%mod;
    

int Lagrange(int n,int *y,int x)
    int ans=0;
    int p=1;
    for(int i=0;i<=n;i++)//分子p
        p=1LL*p*(x-i)%mod;
    
    for(int i=0;i<=n;i++)
        int f=((n-i)&1)?-1:1;//计算符号
        int up=1LL*p*inv[x-i]%mod;
        int down=1LL*finv[i]*finv[n-i]%mod;
        ans=(ans+mod+1LL*f*y[i]*up%mod*down%mod)%mod;
    
    return ans;

signed main()
    init();
    int T;
    scanf("%d",&T);
    while(T--)
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=0;i<=n;i++)
            scanf("%d",&a[i]);
        
        a[n+1]=Lagrange(n,a,n+1);
        n++;
        for(int i=1;i<=n;i++)//计算前缀和,变成多项式S(x)的点
            a[i]+=a[i-1];
            a[i]%=mod;
        
        while(m--)
            int l,r;
            scanf("%d%d",&l,&r);
            if(r<=n)//如果S(l-1),S(r)已知
                printf("%d\\n",(a[r]-a[l-1]+mod)%mod);
            else if(l-1<=n)//如果S(l-1)已知
                printf("%d\\n",(Lagrange(n,a,r)-a[l-1]+mod)%mod);
            else//如果都未知
                printf("%d\\n",(Lagrange(n,a,r)-Lagrange(n,a,l-1)+mod)%mod);
            
        
    
    return 0;