机器学习算法 之 KNN和K-Means

Posted 2022-03-01 June vinvin

目录

• 1.机器学习算法
• • 分类
• 2.KNN算法
• • 2.1 核心思想
  • 2.2 思路
  • 2.3 实现
• 3.K-Means算法
• • 3.1 原理
  • 3.2 过程
  • 3.3 实现
  • 3.4 小结

1.机器学习算法

分类

<1>监督学习
监督学习——根据输入数据（训练数据）学习一个模型，能对后来的输入做预测。其中输入变量和输出变量可以是连续的，也可以是离散的。
回归即：输入变量和输出变量均为连续变量
分类即：输出变量为有限个离散变量
标注即：输入变量与输出变量均为变量序列

算法：分类（类别）、回归（数字）

<2>非监督学习
监督学习：训练数据有标注类别。非监督学习：训练数据没有标注类别。

算法：聚类，降维
聚类基于划分、层次、密度、图形和模型五大类

<3>半监督学习
输入数据同时包含有标记数据和未标记数据。

<4>强化学习
本质是解决决策问题，学会自动进行决策。如下图所示：

算法：马尔科夫决策、动态规划
传统机器学习主要用于数据挖掘、分析。

2.KNN算法

2.1 核心思想

在训练集中选取离输入的数据点最近的k个邻居，根据这个k个邻居中出现次数最多的类别（最大表决规则），作为该数据点的类别。KNN是通过测量不同特征值之间的距离进行分类，属于监督学习中的一种分类方法。

2.2 思路

如果一个样本在特征空间中的k个最相似（即特征空间中最近邻）的样本中的大多数属于某一个类别，则该样本也属于这个类别。
注意：k通常是不大于20的整数；所选择的邻居都是已经正确分类的对象；该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

2.3 实现

import numpy as np
import matplotlib.pyplot as plt
import operator


# 输入数据和类别
def makeData():
    data = np.array([
        [1.0, 1.0],
        [1.0, 1.2],
        [0, 0],
        [0, 0.3]
    ])
    labels = ['A', 'A', 'B', 'B']
    return data, labels


# 分类
def classify(inX, dataset, labels, k):
    dataSize = dataset.shape[0]
    diffMat = np.tile(inX, (dataSize, 1)) - dataset  # 广播
    # 求欧氏距离
    sqDiffMat = diffMat**2
    sqDis = sqDiffMat.sum(axis=1)
    distance = sqDis**0.5
    
    sortedDis = distance.argsort()
    labelCount =   # 存放最终分类结果以及相应的投票数
    for i in range(k):
        votellabel = labels[sortedDis[i]]  # 前k个最近样本的所属类别
        labelCount[votellabel] = labelCount.get(votellabel, 0) + 1  # 统计 前k个最近样本的所属类别 的样本个数
    sortedlabelCount = sorted(labelCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedlabelCount[0][0]


# 显示数据点和颜色
def showData(group, labels):
    labels = np.array(labels)
    index_a = np.where(labels == 'A')
    index_b = np.where(labels == 'B')
    for i in labels:
        if i == 'A':
            plt.scatter(group[index_a][:, :1], group[index_a][:, 1:2], c="red")
        elif i == "B":
            plt.scatter(group[index_b][:, :1], group[index_b][:, 1:2], c="blue")
    plt.show()


if __name__ == '__main__':
    dataset, labels = makeData()
    inX = [0.2, 0.3]
    className = classify(inX, dataset, labels, 3)
    print("该数据属于： %s" % className)
    dataset = np.vstack((dataset, inX))  # 添加新的点
    labels.append(className)  # 添加新的点对应类别
    showData(dataset, labels)

3.K-Means算法

3.1 原理

k-means算法以数据间的距离作为数据对象相似性度量的标准，数据间距离的计算方式对最后的聚类效果有显著影响，常用计算距离方法：余弦距离、欧式距离、曼哈顿距离等。
欧式距离公式：
$$\mathrm{dist}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)=\sqrt{\sum _{\mathrm{d}-1}^{\mathrm{D}}\left({\mathrm{x}}_{\mathrm{i},\mathrm{d}}-{\mathrm{x}}_{\mathrm{j},\mathrm{d}}\right)}$$

3.2 过程

k-means算法属于无监督学习的一种基于划分的聚类算法。
目的：在不知数据所属类别及类别数量的前提下，依据数据自身所暗含的特点对数据进行聚类。

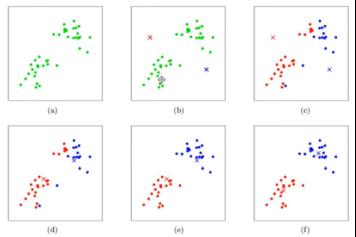
过程：如上图所示，数据样本用圆点表示，每个簇的中心点用叉叉表示：
(a)刚开始时是原始数据，杂乱无章，没有label，看起来都一样，都是绿色的。
(b)假设数据集可以分为两类，令K=2，随机在坐标上选两个点，作为两个类的中心点。
(c-f)演示了聚类的两种迭代。先划分，把每个数据样本划分到最近的中心点那一簇；划分完后，更新每个簇的中心，即把该簇的所有数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”，直到每个簇的中心不在移动为止。(图文来自Andrew ng的机器学习公开课)。

3.3 实现

import numpy as np
import matplotlib.pyplot as plt


# 加载数据
def loadData(fileName):
    data = np.loadtxt(fileName, delimiter='\\t')  # 文本数据以tab间隔，转化为文本
    return data


# 随机出中心点
def randCent(dataSet, k):
    m, n = dataSet.shape
    centids = np.zeros((k, n))
    for i in range(k):
        index = int(np.random.uniform(0, m))
        centids[i, :] = dataSet[index, :]
    return centids


# 欧氏距离
def distEclud(x1, x2):
    return np.sqrt(np.sum((x1-x2)**2))


# K均值聚类
def KMeans(dataSet, k):
    m = np.shape(dataSet)[0]
    clusterAssment = np.mat(np.zeros((m, 2)))  # 第一列存中心点的下标，第二列存数据到中心点的距离 mat可以存字符串
    clusterChange = True

    # 初始化中心点
    centrids = randCent(dataSet, k)
    while clusterChange:
        clusterChange = False
        # 遍历样本（行数）
        for i in range(m):
            minDist = 10000.0
            minIndex = -1
            # 拿到所有的中心点
            for j in range(k):
                # 计算欧式距离
                distance = distEclud(centrids[j, :], dataSet[i, :])
                if distance < minDist:
                    minDist = distance
                    minIndex = j
            # 更新每一行样本所属的中心点
            if clusterAssment[i, 0] != minIndex:
                clusterChange = True
                clusterAssment[i, :] = minIndex, minDist
        for j in range(k):
            # 获取该类别中所有的点
            points = dataSet[np.nonzero(clusterAssment[:, 0] == j)[0]]
            # 求每列的平均值
            centrids[j, :] = np.mean(points, axis=0)
    print("更新完成")
    return centrids, clusterAssment


def show(dataSet, k, centrids, clusterAssment):
    m, n = dataSet.shape
    mark = ['or', 'ob']
    if k > len(mark):
        print("k值太大")
        return 1
    # 绘制样本
    for i in range(m):
        markIndex = int(clusterAssment[i, 0])
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
    mark = ['Dr', 'Db']
    for i in range(k):
        plt.plot(centrids[i, 0], centrids[i, 1], mark[i])
    plt.show()


if __name__ == '__main__':
    dataSet = loadData("test.txt")
    k = 2
    centerios, clus = KMeans(dataSet, k)
    show(dataSet, k, centerios, clus)

3.4 小结

1 初始点选择：初始的聚类中心之间相互距离尽可能远
（1）该类所有数据的均值
（2）随机取k个数据作为类心
（3）选取距离最远的k个点作为类心等

2 迭代过程：
（1）计算所有样本到中心点的距离
（2）比较每个样本到k个中心点的距离，将样本分类到距离最近的类别中
（3）k个类别组成的样本点重新计算中心点

3 迭代终止条件：（1）达到指定的迭代次数；（2）类心不再变化，即收敛

4 k值选取：参考https://www.cnblogs.com/xingnie/articles/10334412.html

5 k-means收敛性：参考https://www.cnblogs.com/zlslch/p/6965209.html

6 复杂度：O(n)，即线性的

7 初始点优化方法：
（1）多次选取中心点进行多次试验，并用损失函数来评估效果
（2）选取距离尽量远的K个样本点作为中心点
（3）对于高维稀疏向量（如文本），可以选取K个两两正交的特征向量作为初始化中心点