数据结构与算法学习笔记(10) 排序

Posted 2022-12-11 临风而眠

数据结构与算法学习笔记(10) 排序

review：

文章目录

• 数据结构与算法学习笔记(10) 排序
• • 一.排序概述
  • • 1.what is 排序
    • 2.排序方法分类
    • • 学习重点
      • 存储结构
  • 二.插入排序
  • • 插入排序的种类
    • • 1.直接插入排序
      • • 性能分析
      • 2.折半插入排序
      • • 算法性能分析
      • 3.希尔排序
      • • 算法性能分析
  • 三.交换排序
  • • 1.冒泡排序
    • • 算法分析
    • 2.快速排序
    • • 算法分析
    • 1.简单的选择排序
    • 2.堆排序
    • • 堆
      • 堆排序
      • • 堆的建立
  • 五.归并排序
  • • • 算法效率分析
  • 六.基数排序
  • • • 算法效率分析
  • 七.排序方法比较
  • • • 时间性能
      • 稳定性
      • 时间复杂度下限

一.排序概述

1.what is 排序

2.排序方法分类

• 按存储介质

• 按比较器个数

• 按主要操作

• 按辅助空间

• 按稳定性

  

  • 排序稳定性的意义
    

• 按自然性

学习重点

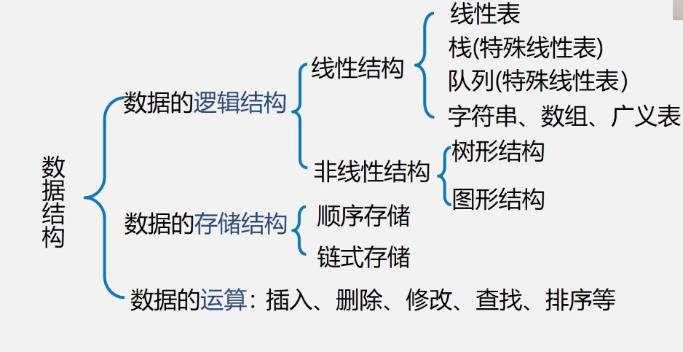
存储结构

二.插入排序

• 基本思想

  每一步将一个待排对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止

  • 边插入边排序，保证子序列随时都是排好序的

• 基本操作：有序插入
  

• 有序插入方法

• 插入的位置

  

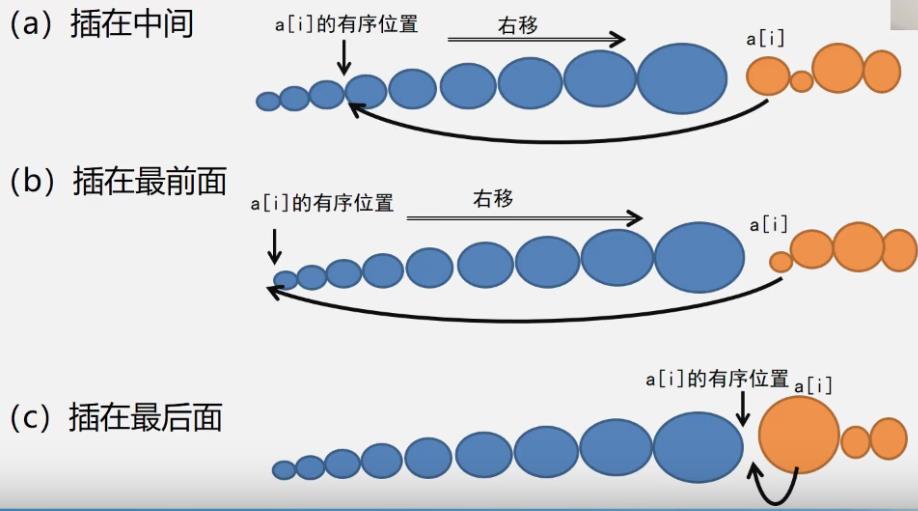
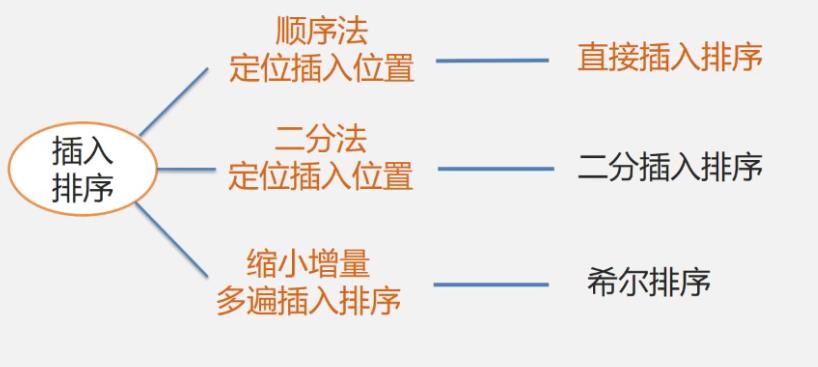
插入排序的种类

1.直接插入排序

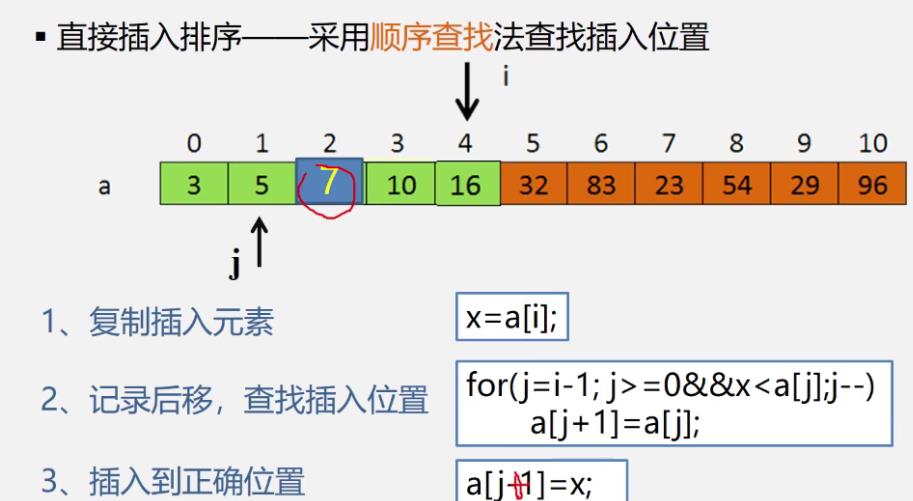
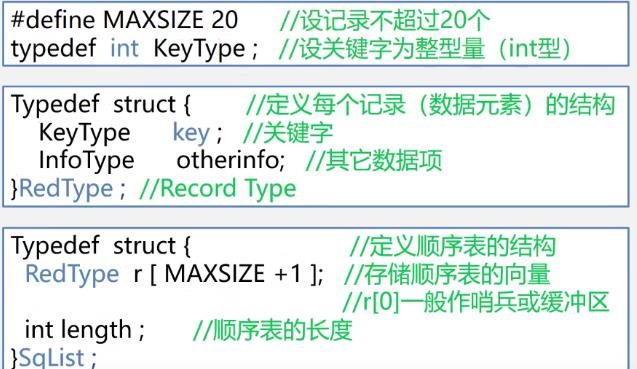
• 使用哨兵

• 算法描述

  void InsertSort( SqList &L ) 
  	int i,j;
  	for(i=2;i<=L.length;++i)
  		if(L.r[i].key<L.r[i-1].key)//若< , 需将L.r[i]插入有序子列
  			L.r[0]=L.r[i]; //复制为哨兵
  			for(j=i-1;L.r[0].key<L.r[j].key;--j)
  				L.r[j+1]=L.r[j];	//记录后移
  			
  			L.r[j+1]=L.r[0];		//插入到正确位置
  			
  		
  	
  
  

性能分析

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Qvl8JGtj-1642063168860)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211112082943.png)]

• 最好的情况

• 最坏的情况

• 平均情况

  

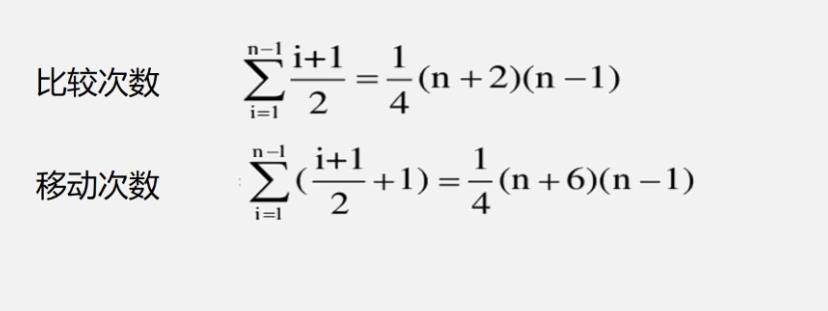
• 时间复杂度结论

  

2.折半插入排序

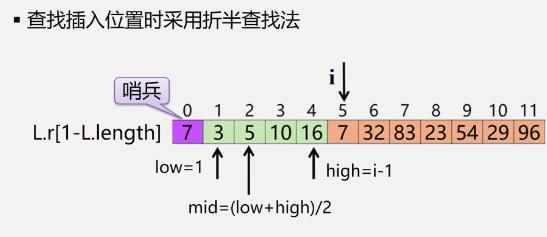
• 算法描述

  void BInsertSort(SqList &L)
  	for(i=2;i<=L.length;++i) //依次插入第2~第n个元素
  		L.r[0]=L.r[i]; //当前插入元素存到"哨兵"位置
  		low=1;	//二分查找法
  		high=i-1;
  		while(low<=high)
  			mid = (low+hight)/2;
  			if(L.r[0].key<L.mid.key)
  			
  				high = mid - 1;
  			
  			else
  			
  				low = mid + 1;
  			//循环结束,high+1为插入位置
  			for(j=i-1;j>=high+1;--j)
  			
  				L.r[j+1] = L.r[j]; 	//移动元素
  			
  			L.r[high+1]=L.r[0];	//插入到正确位置
  		
  	
  
  

算法性能分析

3.希尔排序

• 基本思想

• 例

  

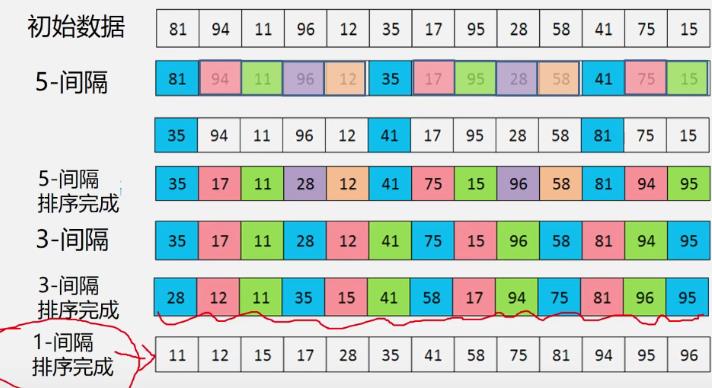
• 希尔排序思路
  

• 希尔排序特点

• 算法描述

  • 主程序

    

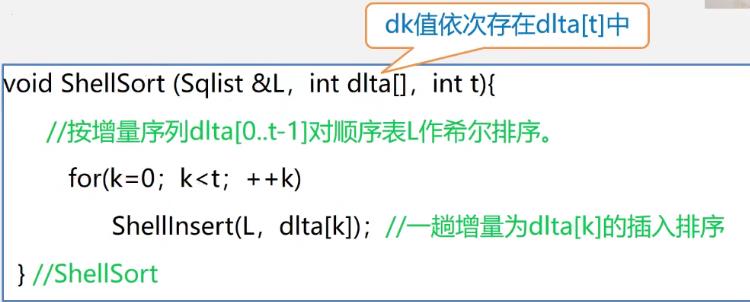
  • 其中某一趟的操作
    

算法性能分析

• 时间效率分析

  

• 稳定性分析

  希尔排序法是一种不稳定的排序算法

  • 例

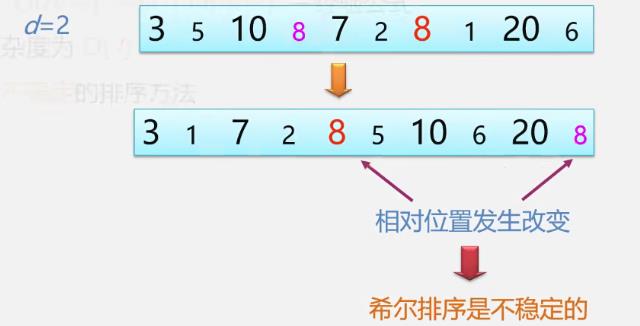
• 总结

  

三.交换排序

• 基本思想

  

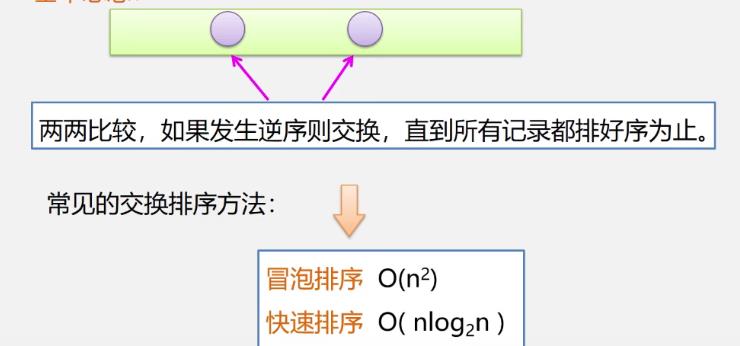
1.冒泡排序

• 基本思想
  

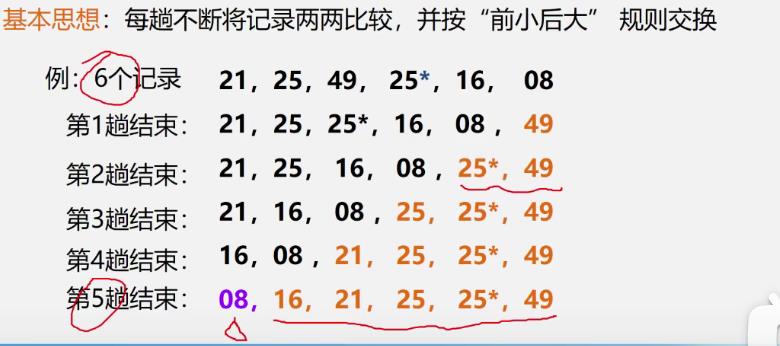
• 比较次数

• 算法描述

  void bubble_sort(SqList &L) //冒泡排序算法
  	int m,i,j;
  	RedType x; //交换时临时存储
  	for(m=1;m<=n-1;m++) //共需要m趟
  		for(j=1;j<=n-m;j++)
  		
  			if(L.r[j].key>L.r[j+1].key)  //若逆序
  				x=L.r[j];
  				L.r[j]=L.r[j+1];
  				L.r[j+1]=x; //交换
  			
  		
  	
  
  
  

• 优点

• 改进

  

  • 例

    

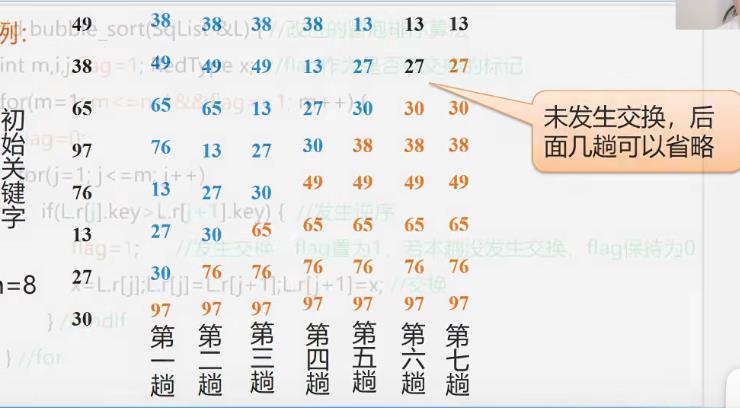
  • 改进算法描述

算法分析

• 时间复杂度

  

• 算法评价

  

2.快速排序

• 基本思想

• 例

  

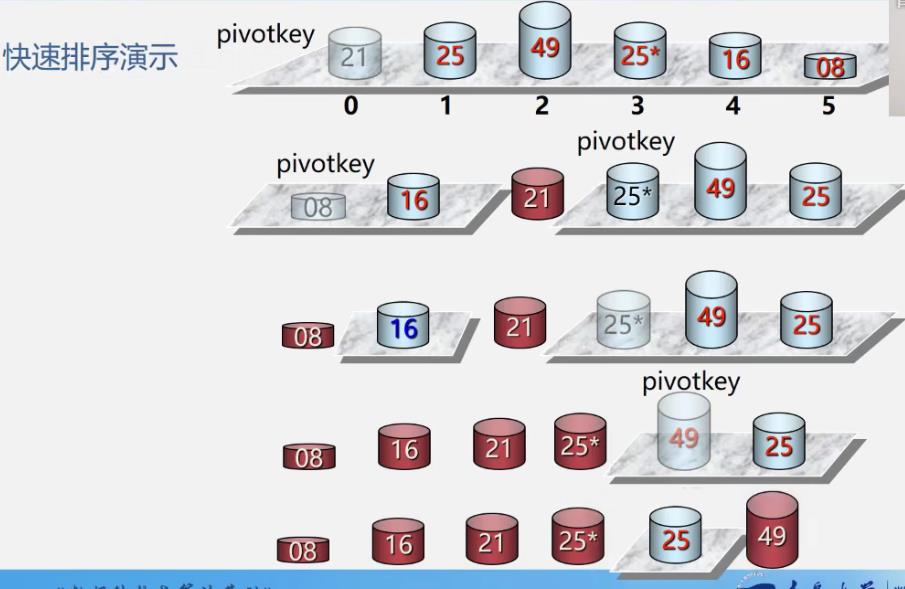
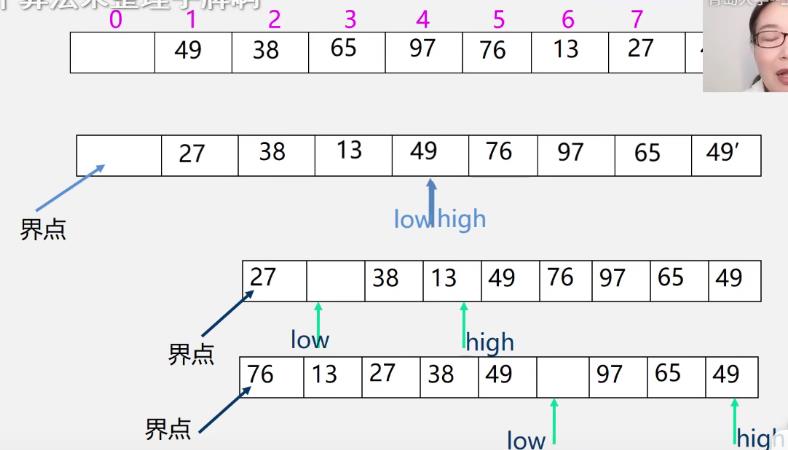
• 特点

  

• 算法描述

  • 主函数

    int main()
    	QSort(L,1,L.length);//对L进行排序,从第一个位置到最后一个位置
    
    

  • 快速排序

    void QSort(SqList &L,int low, int high)
    	if(low<high)//长度大于1
    		pivotloc = Partition(L,low,high);
    		//将L.r[low]到L.r[high]一分为二,pivotloc为枢轴元素排好序的位置
    		QSort(L,low,pivotloc-1);//对低子表递归排序
    		QSort(L,pivotloc+1,high);//对高子表递归排序
    		
    	
    
    

    • 找中心元素

      int Partition(SqList &L,int low,int high)
      	L.r[0]=L.r[low];
      	pivotkey =L.r[low].key;
      	while(low<high)
      		while(low<high&&L.r[high].key>=pivotkey)
              
              --high;
              
              L.r[low] = L.r[high];
              while(low<high&&L.r[low].key<=pivotkey)
              
              ++low;
              
              L.r[high] = L.r[low];
              
          L.r[low]=L.r[0];
          return low;//中心点元素下标
      
      

算法分析

• 时间复杂度

  

• 空间复杂度

  

• 稳定性

• 例

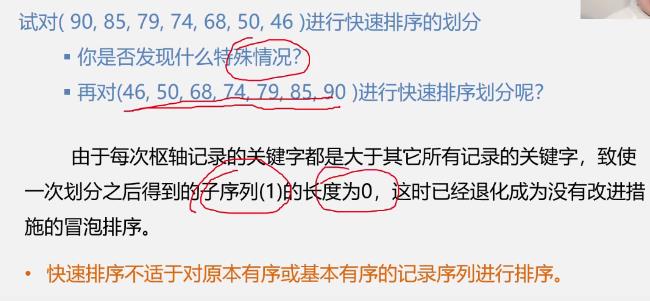
• 影响因素

## 四.选择排序

1.简单的选择排序

• 基本思想与操作

  

• 算法描述

• 时间复杂度分析

  

• 空间复杂度:O(1)

• 算法稳定性

  不稳定排序

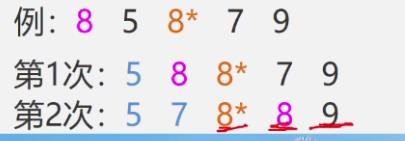
2.堆排序

堆

• 小根堆：每一个结点都比它的左右孩子小

• 大根堆：每一个结点都比它的左右孩子大

• 例

  

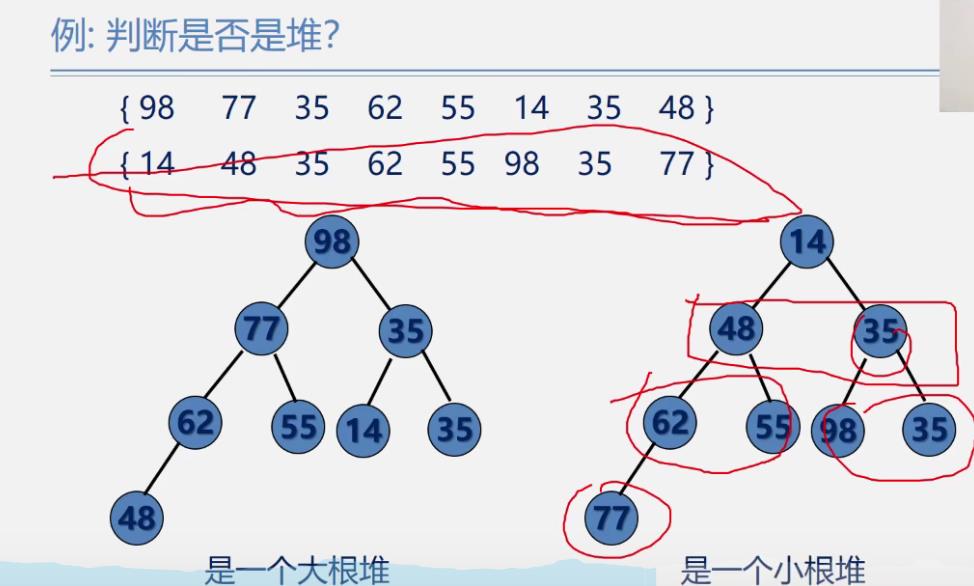
堆排序

• 概念

  

• 堆排序要解决的问题

  [外链图片转存中…(img-imNi8u3p-1642063168885)]

  • 如何在输出堆顶元素后，调整剩余元素为一个新的堆

<img src="https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211116193607.png" alt="image-20211116193607129" style="zoom:50%;" />

堆的建立

如何由无序序列变成堆

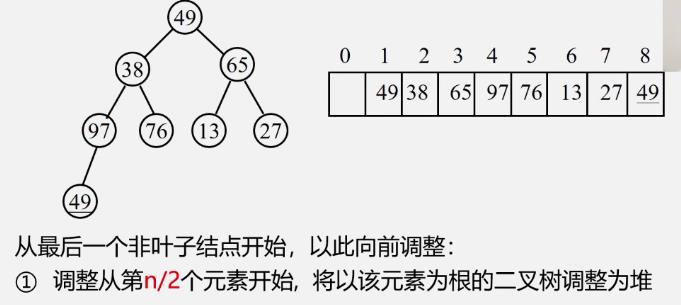
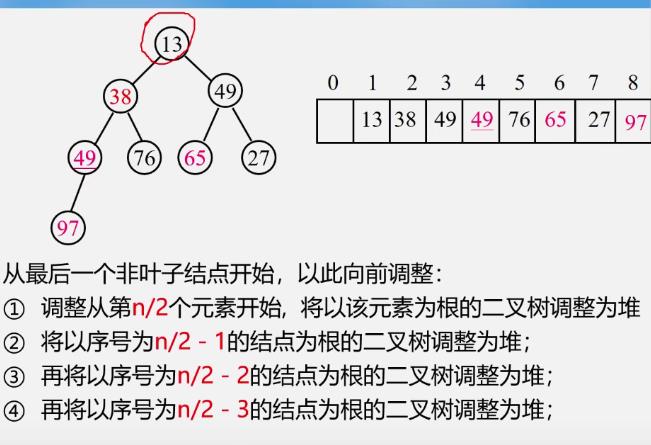
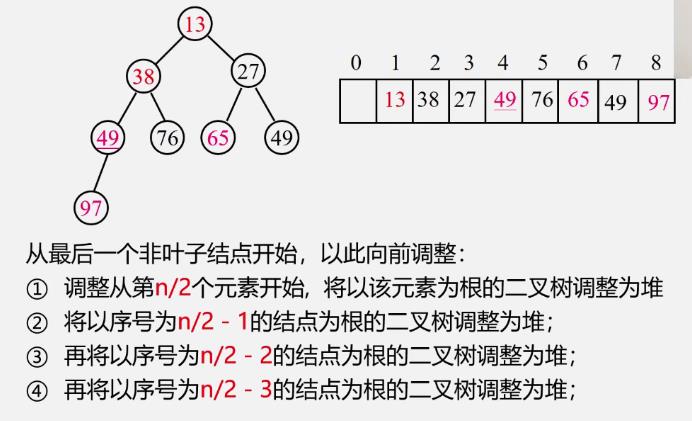
• 算法描述

  

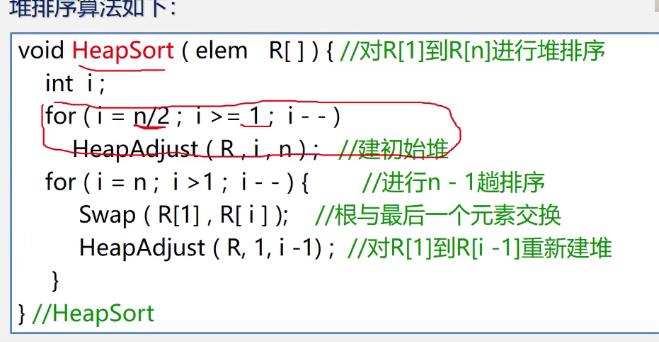
• 算法性能分析

  
  

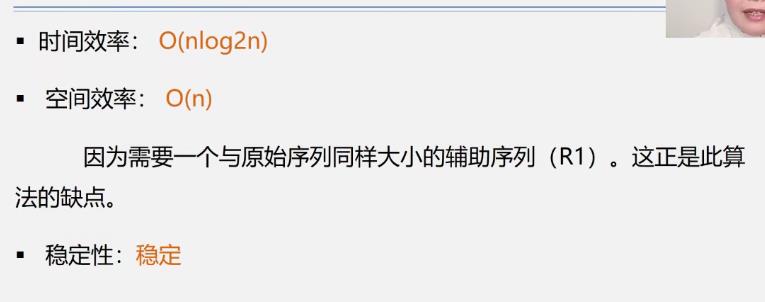
五.归并排序

• 例

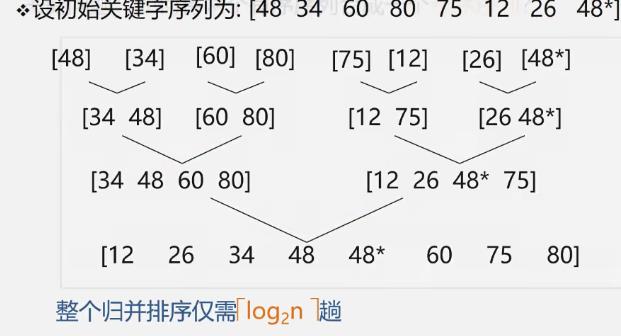
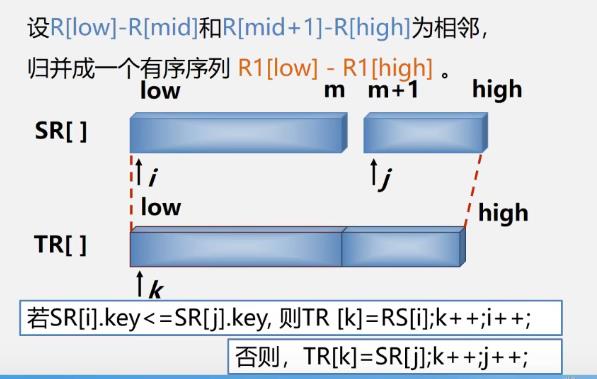
算法效率分析

六.基数排序

• 基本思想：分配+收集

算法效率分析

七.排序方法比较

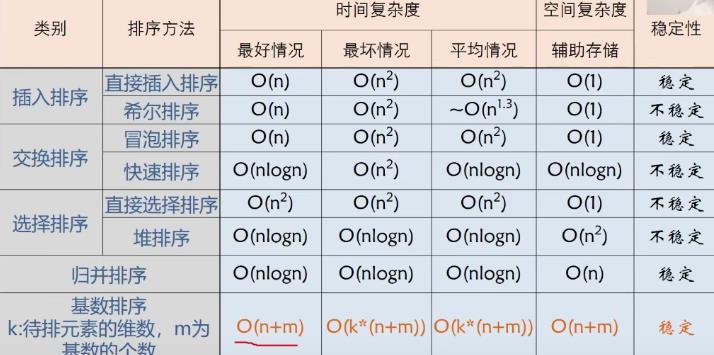
其中堆排序空间复杂度应该是O(1)

时间性能

#### 空间性能

稳定性

时间复杂度下限