数据结构学习笔记(八大排序算法)整理与总结
Posted 康x呀
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记(八大排序算法)整理与总结相关的知识,希望对你有一定的参考价值。
数据结构学习笔记(八大排序算法)整理与总结
排序的相关概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序算法的评价指标: 主要看时间复杂度和空间复杂度(排序所需辅助空间),以及算法本身的复杂度。
排序算法的思维图:

算法复杂度:

排序的思想和实现
这里主要讨论内部排序,排序的手段分为插入、交换、选择、归并、基数排序等。时间复杂度为O(logn)、O(n)、O(n²)的排序成为简单排序,时间复杂度如果出现对数阶,那么就是先进的排序方法。
插入排序
直接插入排序
直接插入排序的思想是指:每次将一个待排序的元素按大小插入到前面己排好序的有序表中,直到全部元素排序完成。最开始默认当前有序表的第0个元素成为一个已经排序好的有序的子数组 直接插入排序的时间复杂度为O( n2 )
以下为直接插入排序的几种方法:
// An highlighted block
//直接插入排序--从前往后比较
void InsertSort_1(int ar[], int left, int right)
{
for(int i=left+1; i<right; ++i)//i从第二个数据开始
{
int k=left;
while(ar[i] > ar[k])
k++;
int tmp = ar[i];//保存要插入的数据
for(int j=i; j>k; --j)
ar[j] = ar[j-1];
ar[k] = tmp;
}
}
//直接插入排序--从后往前比较
void InsertSort_2(int ar[], int left, int right)
{
for(int i=left+1; i<right; ++i)
{
int j = i;
while(j>left && ar[j]<ar[j-1])
{
Swap(&ar[j], &ar[j-1]);//调动函数的话效率会降低
j--;
}
}
}
//直接插入排序--从后往前比较 --不调用交换函数
void InsertSort_3(int ar[], int left, int right)
{
for(int i=left+1; i<right; ++i)
{
int j = i;
int tmp = ar[i];
while(j>left && tmp<ar[j-1])
{
ar[j] = ar[j-1];//数据往后移动
j--;
}
ar[j] = tmp;//当j不小于前边的数据,把tmp的数据交赋给j
}
}
//直接插入排序--从后往前比较 --哨兵位
void InsertSort_4(int ar[], int left, int right)
{
for(int i=left+1; i<right; ++i)
{
ar[0] = ar[i]; //哨兵位
int j = i;
while(ar[0] < ar[j-1])
{
ar[j] = ar[j-1];//移动数据
j--;
}
ar[j] = ar[0];
}
}
哨兵位:
采用哨兵位的直接插入排序,是要将待排序序列的第一个位置留出来设立为哨兵位置,所以需要注意的在定义序列时要多给一个空间。这样做的好处就是不用设立临时变量。
**测试排序的效率**
// An highlighted block
void TestSortEfficiency()
{
srand(time(0));
int n = 10000;
int *a1 = (int*)malloc(sizeof(int) * n);
int *a2 = (int*)malloc(sizeof(int) * n);
int *a3 = (int*)malloc(sizeof(int) * n);
int *a4 = (int*)malloc(sizeof(int) * n);
int *a5 = (int*)malloc(sizeof(int) * n);
for(int i=0; i<n; ++i)
{
a1[i] = rand();//随机数
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
}
unsigned long start = clock();//无符号长整型定义开始的时间
InsertSort_1(a1, 0, n);
unsigned long end = clock();//结束时间
printf("InsertSort_1 : %u\\n", end-start);
start = clock();
InsertSort_2(a2, 0, n);
end = clock();
printf("InsertSort_2 : %u\\n", end-start);
start = clock();
InsertSort_3(a3, 0, n);
end = clock();
printf("InsertSort_3 : %u\\n", end-start);
start = clock();
InsertSort_4(a4, 0, n);
end = clock();
printf("InsertSort_4 : %u\\n", end-start);
start = clock();
BinInsertSort(a5, 0, n);
end = clock();
printf("BinInsertSort : %u\\n", end-start);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
}
总结:直接插入排序简单便捷,容易实现。当待排序记录的数量n很小时,这是一种很好的排序方法。但是当排序序列中记录数量n很大,则不宜采用直接插入排序。可以从“比较”和“移动”这两种操作的次数着手改变。除了基数排序外,每一种排序遵循的一个规则基本上就是“比较,移动”。
折半插入排序
折半插入排序是对直接插入排序的优化,折半插入排序所需附加存储空间和直接插入排序相同,从时间上比较,折半插入排序仅减少了关键字间的比较次数,而记录的移动次数不变。因此,折半插入排序的时间复杂度仍为O(n2)。
折半插入排序减少了比较次数,但是移动的次数还是一样的
// An highlighted block
//折半插入
void BinInsertSort(int *ar, int left, int right)
{
for(int i=left+1; i<right; ++i)
{
int tmp = ar[i];
//二分查找插入位置
int low = left;
int high = i-1;
while(low <= high)
{
int mid = (low + high) / 2;
if(tmp > ar[mid])
low = mid + 1;
else
high = mid - 1;
}
//移动数据
for(int j=i; j>low; --j)
ar[j] = ar[j-1];
ar[low] = tmp;
}
}
总结:
稳定性:稳定
时间复杂度:O(n^2)
希尔排序
概念:希尔排序( Shell’s Sort)又称“缩小增量排序”( Diminishing Increment Sort),是插入排序的一种, 因D.L.Shell 于1959 年提出而得名。直接插人排序,当待排序的记录个数较少且待排序序列的关键字基本有序时,效率较高。希尔排序基于以上两点,从“减少记录个数”和“序列基本有序”两个方面对直接插入排序进行了改进。
基本思想:
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
希尔排序特点:
(1)缩小增量
(2)多遍插入排序
希尔排序步骤:
希尔排序实质上是采用分组插人的方法。先将整个待排序记录序列分割成几组,从而减少参与直接插入排序的数据量,对每组分别进行直接插人排序,然后增加每组的数据量,重新分组。这样当经过几次分组排序后,整个序列中的记录“基本有序”时,再对全体记录进行一次直接插人排序。
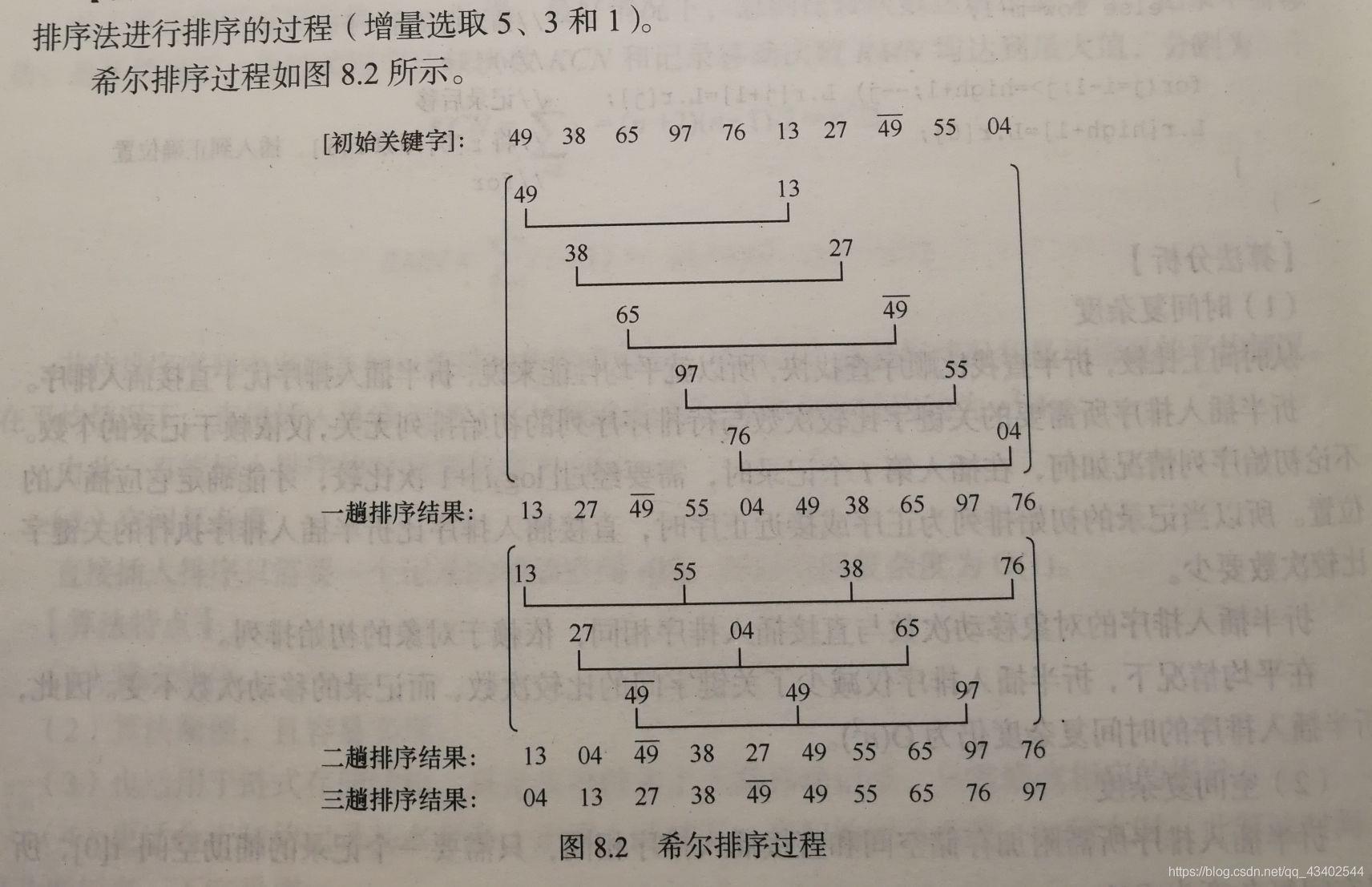
时间复杂度:
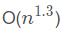
空间复杂度:
O(1)
稳定性:
不稳定 (如图中“上划线49”和“49”的相对位置在排序前后变了,故不稳定)
**希尔排序**
// An highlighted block
void ShellSort(int ar[], int left, int right)
{
int gap = right - left;
while(gap > 1)
{
gap = gap / 3 + 1; //设计文档
for(int i=left+gap; i<right; ++i)
{
if(ar[i] < ar[i-gap])
{
int tmp = ar[i];
int end = i;
while(end>left && tmp<ar[end-gap])
{
ar[end] = ar[end-gap];
end -= gap;
}
ar[end] = tmp;
}
}
}
}
选择排序
直接选择排序
概念:直接选择排序又称简单选择排序,是一种不稳定的排序方法,其是选择排序中最简单一种,其基本思想是:第 i 趟排序再待排序序列 a[i]~a[n] 中选取关键码最小的记录,并和第 i 个记录交换作为有序序列的第 i 个记录。
其实现利用双重循环,外层 i 控制当前序列最小值存放的数组元素位置,内层循环 j 控制从 i+1 到 n 序列中选择最小的元素所在位置 k
具体的排序过程为:
1.将整个记录序列划分为有序区和无序区,初始时有序区为空,无序区含有待排序的所有记录
2.在无序区选择关键码最小的记录,将其与无序区中的第一个元素,使得有序区扩展一个记录,同时无序区减少了一个记录
3.不断重复步骤 2,直到无序区只剩下一个记录为止
**直接插入排序:**
// An highlighted block
int GetMinIndex(int ar[], int left, int right)
{
int min_value = ar[left];
int index = left;
for(int i=left+1; i<right; ++i)
{
if(ar[i] < min_value)
{
min_value = ar[i];
index = i;
}
}
return index;
}
void SelectSort(int ar[], int left, int right)
{
for(int i=left; i<right-1; ++i)
{
int index = GetMinIndex(ar, i, right);
if(index != i)
{
int tmp = ar[i];
ar[i] = ar[index];
ar[index] = tmp;
}
}
}
堆排序
基本思想:
1.首先将待排序的数组构造成一个大堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
构造堆
将无序数组构造成一个大根堆(升序用大根堆,降序就用小根堆)
每次新插入的数据都与其父结点进行比较,如果插入的数比父结点大,则与父结点交换,否则一直向上交换,直到小于等于父结点,或者来到了顶端
固定最大值再构造堆
此时,我们已经得到一个大根堆,下面将顶端的数与最后一位数交换,然后将剩余的数再构造成一个大堆
**堆排序**
// An highlighted block
void _ShiftDown(int ar[], int left, int right, int start)
{
int n = right - left;
int i = start; //父节点
int j = 2*i + 1; //左子树
int tmp = ar[i];
while(j < n)
{
if(j+1<n && ar[j]<ar[j+1])
j++;
if(tmp < ar[j])
{
ar[i] = ar[j];
i = j;
j = 2*i+1;
}
else
break;
}
ar[i] = tmp;
}
void HeapSort(int ar[], int left, int right)
{
//建堆
int n = right - left;
int curpos = (n - 1) / 2 + left;
while(curpos >= left)
{
_ShiftDown(ar, left, right, curpos);
curpos--;
}
//排序
int end = right - 1;
while(end > left)
{
int tmp = ar[end];
ar[end] = ar[left];
ar[left] = tmp;
_ShiftDown(ar, left, end, left);
end--;
}
}
堆排序的时间复杂度为O(nlogn)
空间复杂度为O(1)
综合对比堆排序的效率远比上述其他排序算法高
交换排序
冒泡排序
冒泡排序是比较基础的排序算法之一,其思想是相邻的元素两两比较,较大的数下沉,较小的数冒起来,这样一趟比较下来,最大(小)值就会排列在一端。整个过程如同气泡冒起,因此被称作冒泡排序。
冒泡排序的步骤是比较固定的:
①比较相邻的元素。如果第一个比第二个大,就交换他们两个。
②每趟从第一对相邻元素开始,对每一对相邻元素作同样的工作,直到最后一对。
③针对所有的元素重复以上的步骤,除了已排序过的元素(每趟排序后的最后一个元素),直到没有任何一对数字需要比较。
下面为冒泡排序的三种方式:
// An highlighted block
void BubbleSort_1(int ar[], int left, int right)
{
int n = right - left;
for(int i=0; i<n-1; ++i)
{
for(int j=0; j<n-1-i; ++j)
{
if(ar[j] > ar[j+1])
{
Swap(&ar[j], &ar[j+1]);
}
}
}
}
void BubbleSort_2(int ar[], int left, int right)
{
int n = right - left;
for(int i=0; i<n-1; ++i)
{
for(int j=0; j<n-1-i; ++j)
{
if(ar[j] > ar[j+1])
{
int tmp = ar[j];
while(j<right-1 && tmp>ar[j+1])
{
ar[j] = ar[j+1];
j++;
}
ar[j] = tmp;
}
}
}
}
//记下最后一次交换的位置,后边没有交换,必然是有序的,然后下一次排序从第一个比较到上次记录的位置结束即可
void BubbleSort_3(int ar[], int left, int right)
{
int n = right - left;
bool is_change = false;
for(int i=0; i<n-1; ++i)
{
for(int j=0; j<n-1-i; ++j)
{
if(ar[j] > ar[j+1])
{
int tmp = ar[j];
while(j<right-1 && tmp>ar[j+1])
{
ar[j] = ar[j+1];
j++;
}
ar[j] = tmp;
is_change = true;
}
}
/*如果没有交换过元素,则已经有序,不再进行接下来的比较*/
if(!is_change)
break;
else
is_change = false;
}
}
在冒泡排序中,遇到相等的值,是不进行交换的,只有遇到不相等的值才进行交换,所以是稳定的排序方式
冒泡排序总的平均时间复杂度为O(n2)
冒泡排序适用于数据量很小的排序场景,因为冒泡的实现方式较为简单
快速排序
快速排序也是一种较为基础的排序算法,其效率比冒泡排序算法有大幅提升。因为使用冒泡排序时,一趟只能选出一个最值,有n个元素最多就要执行n - 1趟比较。而使用快速排序时,一次可以将所有元素按大小分成两堆,也就是平均情况下需要logn轮就可以完成排序。
快速排序的思想是:
每趟排序时选出一个基准值,然后将所有元素与该基准值比较,并按大小分成左右两堆,然后递归执行该过程,直到所有元素都完成排序。
快速排序的步骤如下:
①先从数列中取出一个数作为基准数。
②分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
③再对左右区间重复第二步,直到各区间只有一个数。
以下为快速排序的不同版本代码:
// An highlighted block
int GetMidIndex(int ar[], int left, int right)
{
int low = left, high = right-1;
int mid = (low + high) / 2;
if(ar[low]<ar[mid] && ar[mid]<ar[high])
return mid;
if(ar[mid]<ar[low以上是关于数据结构学习笔记(八大排序算法)整理与总结的主要内容,如果未能解决你的问题,请参考以下文章