多路平衡归并和败者树

Posted 2022-12-03 跋扈洋

多路平衡归并和败者树

• 为什么要引入败者树？
• 什么是败者树？
• 后续

为什么要引入败者树？

我们都知道，增加归并路数k能有效减少归并趟数S，进而减少I/O。然而，增加归并路数k时，内部归并的时间将增加。做内部归并时，在k个元素中选取关键字最小的记录需要进行k-1次比较。每趟归并n个元素需要做（n-1）（k-1）次比较，S趟归并总共需要的比较次数是
S(n-1)（k-1）=[log k r] (n-1) (k-1)=[log 2 r] (n-1) (k-1)/[log 2 k]
式中，（k-1）/【log 2 k】随k的增长而增长，因此内部归并时间随k的增长而增长。这将抵消由于增大k而减小外存访问次数所得到的效益。因此，不能使用普通的内部归并排序算法。
为了是内部归并并不受k的增大的影响，引入了败者树。

什么是败者树？

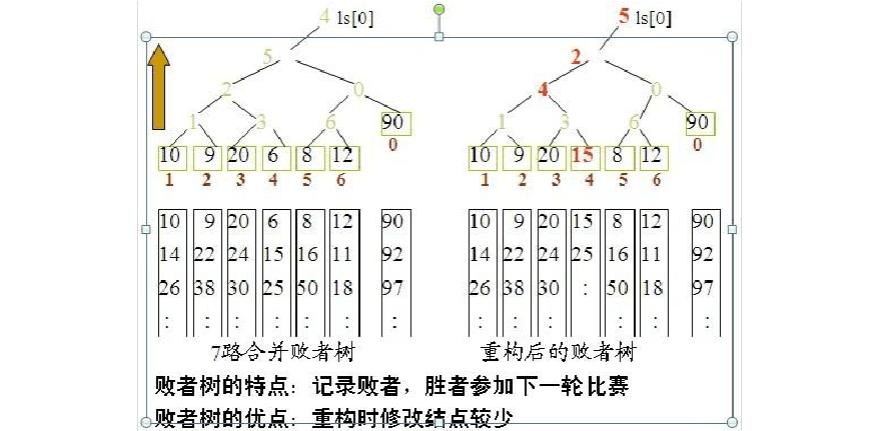
败者树是树形选择排序的一种变体，可视为一棵完全二叉树。k个叶节点分别存放k个归并段在归并过程中当前参加比较的记录，内部节点用来记忆左右子树中的“失败者”，而让胜者往上继续进行比较，一直到根节点。若比较两个数，大的为失败者，小的为胜利者，则根节点指向的数是最小值。


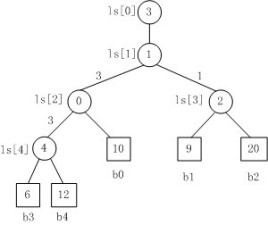
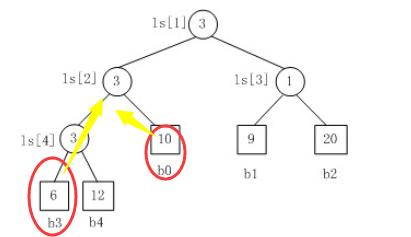
因为k路归并的败者树深度为【log 2 k】，因此k个记录中选择最小关键字，最多需要【log 2 k】比较。所以总的比较次数为
S(n-1)【log 2 k】=[log k r] (n-1)【log 2 k】= (n-1) [log 2 r]
可见，使用败者树后，内部归并的比较次数与k无关了。因此，只要内存空间允许，增大归并路数k将有效地减少归并树的高度，从而减小I/O次数，提高外部排序的速度。
需要说明的是，归并路数k并不是越大越好。归并路数k增大时，相应的需要增加输入缓冲区的个数。若可供使用的内存空间大小不变，势必要减少每个输入缓冲区的容量，使得内存、外存交换数据的次数增大。当k值过大时，虽然归并趟数会减少，但读写外存的次数仍会增加。

后续

如果想了解更多物联网、智能家居项目知识，可以关注我的程序设计专栏。
订阅专栏后，可以在微信公众号上私聊我，直接发给你源码。
或者关注公众号。

编写不易，感谢支持。