聚类算法 - kmeans

Posted 2023-05-10

参考技术A

kmeans即k均值算法。k均值聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

简易动画过程在这， 传送门
第一步 ，输入k的值，即我们希望将数据集经过聚类得到k类，分为k组
第二步 ，从数据集中随机选择k个数据点作为初识的聚类中心（质心，Centroid）
第三步 ，对集合中每一个数据点，计算与每一个聚类中心的距离，离哪个中心距离近，就标记为哪个中心。待分配完全时，就有第一次分类。
第四步 ，每一个分类根据现有的数据重新计算，并重新选取每个分类的中心（质心）
第五至N步 ，重复第三至四步，直至符合条件结束迭代步骤。条件是如果新中心和旧中心之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，终止迭代过程。

该算法的核心就是选择合适的k值，不同的k值出来有不同的结果。

手肘法的核心指标是SSE(sum of the squared errors，误差平方和)，

其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。

手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

该方法的核心指标是轮廓系数（Silhouette Coefficient），某个样本点Xi的轮廓系数定义如下：

其中，a是Xi与同簇的其他样本的平均距离，称为凝聚度，b是Xi与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是

其中p是某个簇Ck中的样本。事实上，简单点讲，就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。

求出所有样本的轮廓系数后再求平均值就得到了 平均轮廓系数 。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

（1）容易理解，聚类效果不错，虽然是局部最优， 但往往局部最优就够了
（2）处理大数据集的时候，该算法可以保证较好的伸缩性
（3）当簇近似高斯分布的时候，效果非常不错
（4）算法复杂度低

（1）K 值需要人为设定，不同 K 值得到的结果不一样
（2）对初始的簇中心敏感，不同选取方式会得到不同结果
（3）对异常值敏感
（4）样本只能归为一类，不适合多分类任务
（5）不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类

基于R语言的Kmeans聚类算法

题记：本文是个人的读书笔记，仅用于学习交流使用。

01

解决什么问题

      本节介绍一下Kmeans聚类，也叫K均值聚类或者是动态聚类法。k-means算法也属于无监督学习的一种聚类算法。采用R语言详细描述Kmeans实现过程。

      这种聚类方法的优势在于，对于大样本的聚类，具有计算量小，占用计算机内存较少和方法简单的优点。

02

算法思想

     假设我们要把数据分成k个类，大概可以分为以下几个步骤：

              1. 随机选取k个点，作为每个类别的类心；

              2.分别计算每个点到这k个中心的距离(点与点的距离计算)，将该点分到最近的                   聚类中心，这样就形成了k个簇；

              3.更新每个簇的类心（均值）；

              4.重复以上2~3步，直到类心的位置不再发生变化或者达到设定的迭代次数。

       

        其中第三步是：类心的计算公式如下，其中表示第k类，表示第k类中数据对象的个数：

            第四步类心的迭代公式：

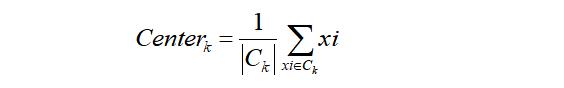
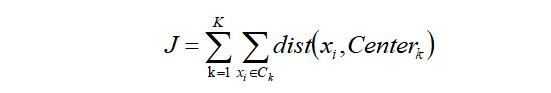
       下面我们通过一个具体的例子来理解这个算法，假设我们首先拿到了这样一个数据，要把它分成两类：

         1.下图中，人眼可以很快的分辨出来，可以在两个聚类间找到一条合理的分界线。

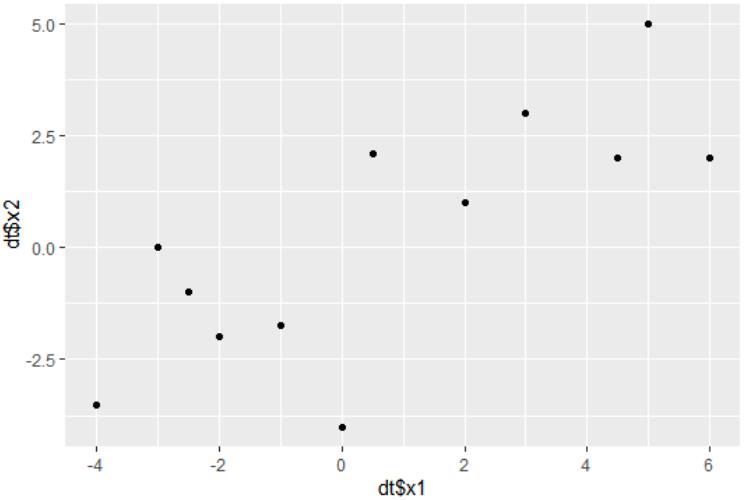
            2.首先我们随机选取样本中任意两个点作为聚类中心。根据选取的两点，通过第一次迭代，将图中黑色的点归为一类，蓝色的点归为另一类。

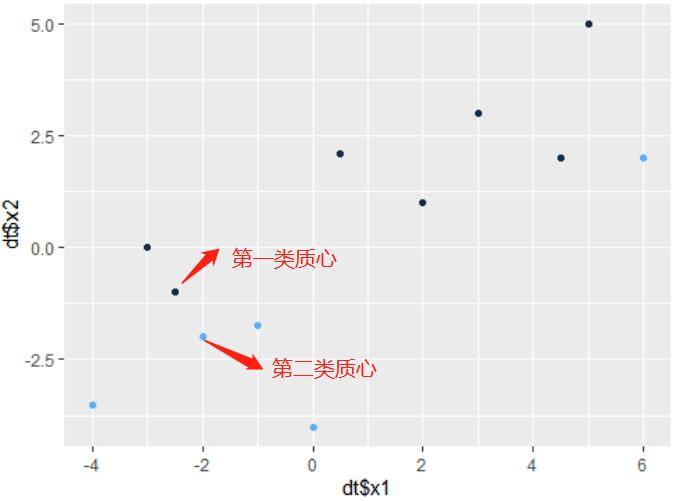
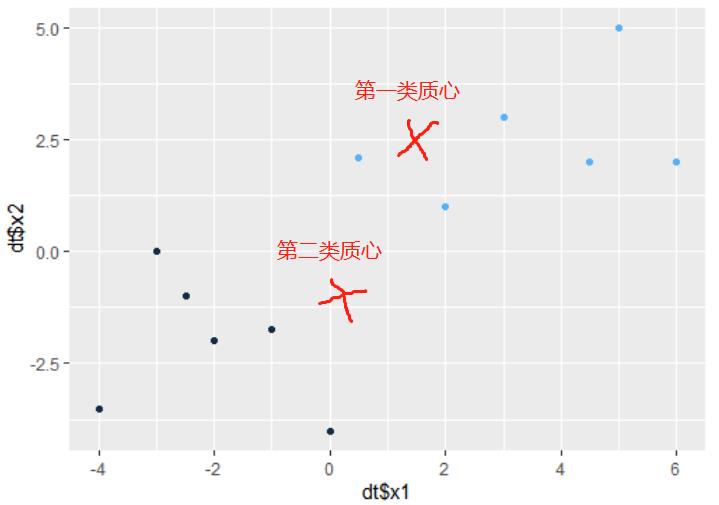
      3.根据第一次迭代将生成的两类数据，分别求出每个簇的类心。相当于原理第三步。并再次计算每个点与新的类心距离，将点分到最近的类心。

      由图可以看到经过第二次迭代，数据正确分成2簇。

      采用R代码将上述算法原理详细实现一遍，更多采用python写，清楚了原理，用哪种语言写，都是很随意的。当然R里面有封装的好的Kmeans函数，一句代码就做完所有的事，但还是建议大家，自己写一遍算法，有助于理解。

### Kmeans 均值聚类#为给定数据集构建一个包含K个随机质心的集合randcent <- function(dt,k){ centroids <- as.data.frame(matrix(0,nrow = k,ncol=ncol(dt))) colnames(centroids) <- colnames(dt)  for(i in 1:k){ index <- sample(1:nrow(dt),1,replace =T) centroids[i,] <- dt[index,] } return(centroids)}

        建立一个对象，存放样本点所属簇和每个样本点与类心的距离。

 #行的数目# 第一列存样本属于哪一簇# 第二列存样本的到簇的中心点的误差(用距离表示)clusterAssment = data.frame(class = rep(0,nrow(dt)),                 error = rep(0,nrow(dt)))

       编写Kmeans算法：

kmeans_fit <- function(dt,k){clusterAssment = data.frame(class = rep(0,nrow(dt)), error = rep(0,nrow(dt))) clusterChange = T # 第1步 初始化centroids centroids = randcent(dt,k=2) step=1 while(clusterChange){ clusterChange = F # 遍历所有的样本（行数） for(i in 1:nrow(dt)){ minDist = 100000.0      minIndex = -1      # 遍历所有的质心       #第2步 找出最近的质心 for(j in 1:k){ dt_ <- rbind(dt[i,],centroids[j,]) d <- dist(dt_) if(d < minDist){ minDist <- d; minIndex<- j} } # 第 3 步：更新每一行样本所属的簇 if(clusterAssment[i,1]!= minIndex){ clusterChange = T clusterAssment[i,1] <- minIndex clusterAssment[i,2] <- minDist } } #第 4 步：更新质心 for(i in 1:k){ loc <- which(clusterAssment[,1]==i)  pointsIncluster <- dt[loc,] # 获取簇类所有的点 centroids[i,] <- apply(pointsIncluster,2,mean) ##对数据集的列就均值 } step=step+1 ##观察迭代次数 print(step) } print("Congratulations,cluster complete!") re <- list(centroids=centroids,clusterAssment=clusterAssment) return(re)}

        运行这个简易的算法模型

dt <- data.frame(x1 = c(5,6,4.5,0.5,2,-3,-2.5,-2,0,-4,3,-1), x2=c(5,2,2,2.1,1,0,-1,-2,-4,-3.5,3,-1.75))re <- kmeans_fit(dt,2)###查看运行完的结果re$centroids;re$clusterAssment  ## 可查看所属簇和类心library(ggplot2)qplot(dt$x1,dt$x2,color=clusterAssment$class) ###画图

04

案例实战

       03部分，我们采用一个小例子拆解了Kmeans的基本算法原理，接下来我们可以拿这个代码跑一遍 中的葡萄酒案例，跟层次聚类的结果对比一下，匹配效果达到95%，效果还是不错的。请注意之所以让K=3也是继承了之前的最优聚类个数的选择。

library(HDclassif) #contains the dataset ##葡萄酒数据集data(wine)names(wine) <- c("Class", "Alcohol", "MalicAcid", "Ash", "Alk_ash", "magnesium", "T_phenols", "Flavanoids", "Non_flav",                 "Proantho", "C_Intensity", "Hue", "OD280_315", "Proline")df <- as.data.frame(scale(wine[, -1]))re <- kmeans_fit(df,3)table(re$clusterAssment[,1],wine$Class) ###匹配度达95%

05

Kmeans()函数详解

       接下来我们用R自带的Kmeans函数跑一遍这个葡萄酒数据集，首先介绍一下Kmeans()函数：

kmeans(x, centers, iter.max = 10, nstart = 1,algorithm = c("Hartigan-Wong", "Lloyd","Forgy", "MacQueen"))

其中：

1.待聚类样本组织在x指定的矩阵或数据框中。

2.参数centers：若为一个整数，则表示聚类数目K；若为一个矩阵（行数等于聚类数目K，列数等于聚类变量个数），则表示初始类质心，每一行表示一个初始类质心。

3.参数iter.max用于指定最大迭代次数，默认为10次。R中仅以最大迭代次数作为终止迭代条件。

4.当参数为centers为一个整数时，R将采用随机选择法从数据中抽取K个观测值作为初始类质心。我们，不同的初始类质心对最终的聚类结果是存在影响的。所以，R为克服大数据集下终止迭代次数不充分大时，初始类质心抽取的随机性对聚类结果的影响，可指定参数nstar为一个大于1的值（默认为1），表示重复多次抽取质心。

5.参数algorithm，用于指定迭代算法，其中"Lloyd"是经典的算法，就是上面自己编写代码的实现过程，但这种算法针对不平衡数据效果不太好，而"Hartigan-Wong"则是改进的针对不平衡数据的算法，作为默认算法。每一种算法的实现过程，有兴趣的朋友可以参看参考文献3。

返回结果解释：

Kmeans函数的返回结果是一个列表，包括如下成分：

1.cluster：存储各观测所属的类别编号，也称聚类解。

2.centers：存储各个类的最终类质心。

3.totss：所有聚类变量的离差平方和之和，是对类内部观测数据点离散程度的测度。

4.cotwithss：每个类内所有聚类变量的离差平方和之和的总和。

5.betweenss：各类别间的聚类变量离差平方和之和

6.size：各类的样本量。

Kmeans聚类

     现在选择3个簇进行Kmeans聚类，现在计算距离矩阵，并建立层次聚类模型。如下所示：

set.seed(1234) ##设定随机数种子km <- kmeans(scale(df), 3, nstart = 25)  #设置随机分配的参数nstart

    对比K均值聚类结果和品种等级：

table(km$cluster, wine$Class)

      这个表中，聚类结果匹配了96%的品种等级。与层次聚类的ward.D2相比，这两种方法效果相似，因此可以将任意一种作为最优的聚类方法。

06

总结

          以上是针对全部是数值型的数据做的分类，用R语言实现是非常简单的。如果数据里面既有数值型，又有非数值型，用什么聚类方法呢？后面有机会再跟大家介绍另外集中聚类方法。

参考文献

1. 薛毅等.统计建模与R软件.清华大学出版社
   

2. Cory Leismester.精通机器学习.基于R.人民邮电出版社

3. https://blog.csdn.net/joeland209/article/details/72147763

作介绍：医疗大数据统计分析师,擅长R语言。

欢迎各位在后台留言，恳请斧正！

更多阅读

长按二维码

易学统计