迪杰斯特拉算法的算法思想

Posted 2023-05-07

参考技术A

按路径长度递增次序产生算法：
把顶点集合V分成两组：
（1）S：已求出的顶点的集合（初始时只含有源点V0）
（2）V-S=T：尚未确定的顶点集合
将T中顶点按递增的次序加入到S中，保证：
（1）从源点V0到S中其他各顶点的长度都不大于从V0到T中任何顶点的最短路径长度
（2）每个顶点对应一个距离值
S中顶点：从V0到此顶点的长度
T中顶点：从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度
依据：可以证明V0到T中顶点Vk的，或是从V0到Vk的直接路径的权值；或是从V0经S中顶点到Vk的路径权值之和
（反证法可证）
求最短路径步骤
算法步骤如下：
G=V,E
1. 初始时令 S=V0,T=V-S=其余顶点，T中顶点对应的距离值
若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值
若不存在<V0,Vi>，d(V0,Vi)为∞
2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W，加入到S中
3. 对其余T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值缩短，则修改此距离值
重复上述步骤2、3，直到S中包含所有顶点，即W=Vi为止

迪杰斯特拉算法解析

       迪杰斯特拉算法是解决单源最短路径（从图中的某个顶点到其余顶点的最短路径）的一种常用算法，是一种按照路径长度递增的次序分别产生到各顶点最短路径的贪心算法，

       算法思想：

     1.初始时，集合s仅包含源点v0,集合v-s中包含除了v0以外的所有顶点，v0到v-s中各顶点的路径长度或者为某个权值(如果他们之间有弧相连)，或者为oo(没有弧相连)。

      2.按照最短路径长度递增的次序，从集合v-s中选出到顶点v0路径长度最短的顶点Vk加入到集合s中。

      3.加入Vk之后，为了寻找下一个最短路径，必须修改从v0到集合v-s中剩余顶点Vi的最短路径，若在路径Vk加上之后，使得v0到Vi的路径长度比原来没有加入Vk时的路径长度短，则修正v0到Vi的路径长度为其中较短的一条距离。

      4.重复以上步骤，直到集合v-s中的顶点全部加入到集合s中为止。

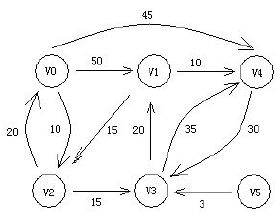
 对于以下图：

      

具体分析过程如下：