理解what、why、how，才能知行合一
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了理解what、why、how，才能知行合一相关的知识，希望对你有一定的参考价值。
参考技术A 相信大家都知道what、why、how吧？简单来说，就是：
1.what（是什么）
2.why（为什么）
3.how（怎么办）
但是，很多人提出的问题，却并不是真正的问题，而是一个他试图用来解决真正问题的答案。
就好比，这个问题：我怎么才能给我的高管降薪？
相信大家听到这个问题后，肯定会围绕着这个问题来提问，比如：你给他降薪他有可能会离开，你希望他离开吗？
我们会试图给这个问题找到答案，但是，我们可以这样想一想：为什么他会提出给高管降薪这个问题呢？
所以，我们需要理解他为什么会提出这样的问题。
正如他提出这个问题的原因，是因为他的公司要上市了，在一次采访中，对方问公司的愿景是什么，价值观是什么，战略方向是什么，未来要做什么事情，但是他公司的五个高管的回答都不一样。
这让他很恼火，因为这五个高管是他花了大价钱从外面请来的，但是业绩做的不是很好，远远没达到他的预期，而且，这五个高管对于公司的愿景、价值观等问题的认识，居然都没有达成一致，所以，他才决定给他们降薪，因为他觉得他们不值现在的价钱。
了解了前因后果，我们可以知道，他提出来的根本不是问题，而是他想出来的能解决问题的答案。
所以，我们在提出问题的时候，需要先了解why，只有了解了why，才能真正理解what和解决how。
因为，能够在描述事情的时候，能把what、why、how区分清楚，对一个人来说，就是一个巨大的提升。
what、why、how，是“黄金三问”，密不可分，只有真正的吧what、why、how这“黄金三问”同时解决了，才能真正做到王阳明所说的“知行合一”。
愿我们都能知道很多道理，也能过好自己的一生。
[What-Why-How] 线性回归预测
What
现有多个变量X1, X2, X3, ....会对结果数据Y产生影响，现在要求出这些变量Xn对于最终结果的影响权重。找到一个线(两个变量)，面(三个变量)来拟合这些权重的数值。通过训练数据得到这些参数，然后使用这些参数(模型)对新数据进行预测
例如，拟合一个平面：
其中 θ0表示预置的权重参数。
-
误差
真实值和预测值之间肯定是要存在差异的
误差是独立并且具有相同分布，并且服从均值为0方差为θ2的高斯分布（正态分布）
似然函数：
，什么样的参数跟我们的数据组合后恰好时真实值。 样本数据 -> 参数，参数估计。最大似然函数，极大似然估计，让结果符合真实值的概率最大。
对数似然：
，似然函数的对数形式，便于计算。
目标函数：
，从对数似然化简得出，目标函数值越小似然函数值越大。对目标函数求偏导，在其偏导数为0点的，为极小值点：
-
评估方法
最常用的评估项：R2，其值越接近1认为结果约好。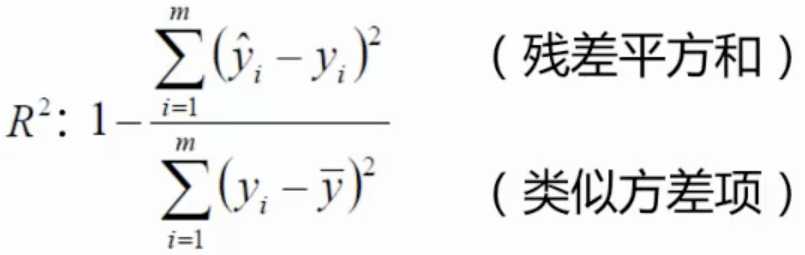
-
梯度下降
得到一个目标函数后，如何进行求解。
目标函数：
，寻找山谷最低点，即函数终点
如果有多个参数，是每个参数分布求极值，每次一小点，不断的更新参数
梯度下降的方法：
-
-
批量梯度下降
-
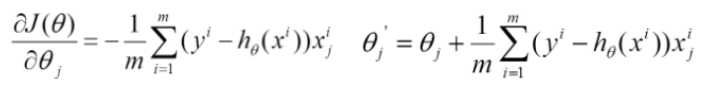
容易得到最优解，但每次要考虑所有样本，速度很慢
-
-
随机梯度下降
-
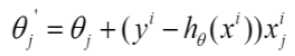
每次找一个样本，迭代速度快，但不一定每次朝着收敛的方向
-
-
小批量梯度下降 batch
-
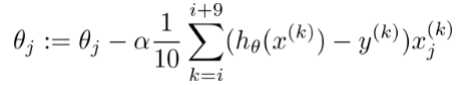
每次更新选择一小部分数据来计算，较实用
不同步长(学习率)对结果会有大影响。一般要小一些，从小值开始，不行再小。批量的大小，在机器资源允许的情况下尽量大些。
Why
How
以上是关于理解what、why、how，才能知行合一的主要内容，如果未能解决你的问题，请参考以下文章