数学概率随机变量X服从拉普拉斯分布,其概率密布为f(x)=(1/2)e^-x计算E(x),D(x)

Posted 2023-04-24

求求D(X)详细的过程....

参考技术A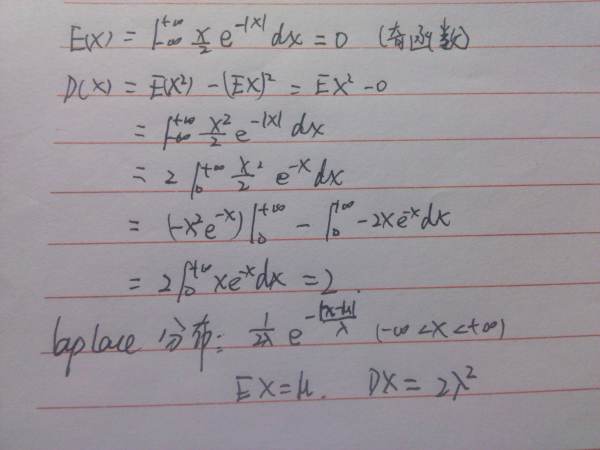

本回答被提问者采纳

高斯分布

数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

离散型

离散型随机变量的一切可能的取值与对应的概率成绩之和称为称为该离散型随机变量的数学期望^{(若该求和绝对收敛），记为。}
它是简单算术平均的一种推广，类似加权平均。

数学期望公式

离散型随机变量X的取值为，为X对应取值的概率，可理解为数据
出现的频率
则：

 

 

性质

设C为一个常数，X和Y是两个随机变量。以下是数学期望的重要性质：

1.

2.

3.

4.当X和Y相互独立时，

 

方差的定义

方差在统计描述和概率分布中各有不同的定义，并有不同的公式。

在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：

为总体方差，

为变量，

为总体均值，

为总体例数。

实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：

S^2= ∑(X-) ^2 / (n-1)^[2]

S^2为样本方差，X为变量，为样本均值，n为样本例数。

在概率分布中，设X是一个离散型随机变量，若E{[X-E(X)]^2}存在，则称E{[X-E(X)]^2}为X的方差，记为D(X),Var(X)或DX，其中E(X)是X的期望值，X是变量值^[1]  ，公式中的E是期望值expected value的缩写，意为“变量值与其期望值之差的平方和”的期望值。^[2]  离散型随机变量方差计算公式：

D(X)=E{[X-E(X)]^2}=E(X^2) - [ E(X)]^2

当D(X)=E{[X-E(X)]^2}称为变量X的方差，而

称为标准差（或均方差）。它与X有相同的量纲。标准差是用来衡量一组数据的离散程度的统计量^[3]  。

对于连续型随机变量X，若其定义域为(a,b)，概率密度函数为f(x)，连续型随机变量X方差计算公式：

D(X)=(x-μ)^2 f(x) dx^[2]

方差刻画了随机变量的取值对于其数学期望的离散程度。（标准差、方差越大，离散程度越大)

若X的取值比较集中，则方差D(X)较小,若X的取值比较分散，则方差D(X)较大。

因此，D(X)是刻画X取值分散程度的一个量，它是衡量取值分散程度的一个尺度。

 

方差的性质

D(X)=E{[X-E(X)]^2}=E(X^2) - [ E(X)]^2

 

1、设C是常数，则D（C）=0

2、设X是随机变量，C是常数，则有

3、设 X 与 Y 是两个随机变量，则

其中协方差

特别的，当X，Y是两个不相关的随机变量则

此性质可以推广到有限多个两两不相关的随机变量之和的情况。

4、D(X)=0的充分必要条件是X以概率1取常数E（X），即

（当且仅当X取常数值E（X）时的概率为1时，D（X）=0。）

注：不能得出X恒等于常数，当x是连续的时候X可以在任意有限个点取不等于常数c的值。

5、D(aX+bY)=a²DX+b²DY+2abCov(X,Y)。

 

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

定义

正态分布一维正态分布

若随机变量

服从一个位置参数为

、尺度参数为

的概率分布，且其概率密度函数为^[2]

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作

，读作服从，或服从正态分布。

μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。

本词条的正态分布是一维正态分布，此外多维正态分布参见“二维正态分布”。

正态分布标准正态分布

当

时，正态分布就成为标准正态分布

 

 

正态分布有两个参数，即期望（均数）μ和标准差σ，σ²为方差。

正态分布公式

正态分布具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ,σ²)。

μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。

σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。