基于负相关学习多神经网络集成的目标识别算法MATLAB仿真
Posted fpga和matlab
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于负相关学习多神经网络集成的目标识别算法MATLAB仿真相关的知识，希望对你有一定的参考价值。
目录
一、理论基础
学习方法的泛化能力、学习效率和易用性是机器学习及其应用过程中所面临的三个关键性挑战问题。神经网络集成学习通过训练多个神经网络并将其结果进行合成,显著地提高了学习系统的泛化能力,成为近年来机器学习领域一个重要的研究方向。在分析神经网络集成方法研究现状的基础上,以实验设计、粗集理论、特征加权以及并行技术等为支撑,围绕神经网络集成学习方法的易用性、泛化能力和学习效率等问题展开研究,提出了更有效的神经网络集成方法,并将其应用到地震预报领域。神经网络集成的结构(个体网络的数目和个体网络的结构)和个体网络的训练参数(如训练次数和学习率等)关系到集成性能的好坏,同时影响着集成是否易于被使用。本文首先研究了实验设计在神经网络集成中的应用,提出了一种简单、科学地确定神经网络集成结构和个体网络的训练参数的方法。使用者可以用较少的实验次数,分析影响神经网络集成泛化能力的因素以及确定各因素用什么水平搭配起来对集成的泛化能力最佳。同时,通过最近
公式1：
对应程序为：
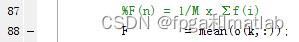
公式2：
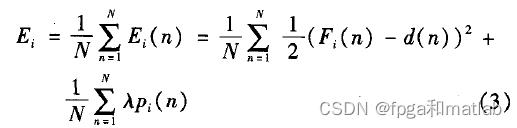
对应程序为：
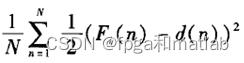和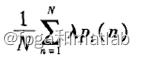
分别对应的程序为：
和
公式3：
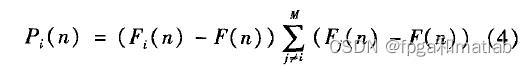
对应的程序为：
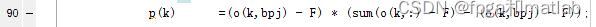
公式4：
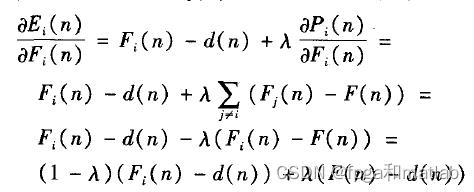
对应的程序为：
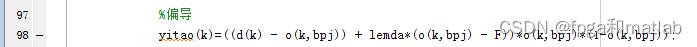
其余的和多集成BP神经网络的相关理论相似，这里不做进一步的介绍了。
二、案例背景
负相关学习是 通过 一个惩罚 项加强集成 网络 中个 体 网络之间的差异度，下面对该算法作简单说明。
三、MATLAB核心代码
该神经网络的顶层函数如下：
clc;
clear;
close all;
warning off;
RandStream.setDefaultStream(RandStream('mt19937ar','seed',1));
%加载数据
load australian.dat
data = australian;
%输入数据预处理
SET = [1:14];
for i = SET
P(:,i) = data(1:100,i)/max(data(1:100,i));
end
[P,minp,maxp] = premnmx(P);
T = data(1:end,end);
% P = rand(200,1);
% T = round(P);
Len = length(P);
%输入层节点
NI = size(P,2);
%输出层节点
No = 1;
%隐层节点
Nh = 14;
%最大迭代次数
Max_iteration = 3000;
%目标精度
Paim = 1e-3;
%学习率设定值
Learning_Rate = 0.5;
error = 0;
error2 = zeros(1,Len);
%BP1~4
KER = 4;%集成个数
W0 = rand(NI,Nh,KER);
deltaW0 = zeros(NI,Nh,KER);
dW0 = zeros(NI,Nh,KER);
W = rand(Nh,No,KER);
deltaW = zeros(Nh,No,KER);
dW = zeros(Nh,No,KER);
ERR = [];
Index = 1;
while(Index<=Max_iteration)
Index
jj=1;
error2 = zeros(Len,KER);
while(jj<=Len)
for k=1:No;
d(k)=T(jj);
end
for i=1:NI;
x(i)=P(jj,i);
end
%集成多个BP神经网络
for bpj = 1:KER
for j=1:Nh%BP前向
net=0;
for i=1:NI
net=net+x(i)*W0(i,j,bpj); %加权和∑X(i)V(i)
end
y(j)=1/(1+exp(-net));
end
for k=1:No
net=0;
for j=1:Nh
net=net+y(j)*W(j,k,bpj);
end
%输出值
o(k)=1/(1+exp(-net));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
errortmp=0.0;
for k=1:No
errortmp=errortmp+(d(k)-(o(k)))^2;%传统的误差计算方法
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
error2(jj,bpj)=0.5*errortmp/No;
for k=1:No%BP反向计算
yitao(k)=(d(k)-o(k))*o(k)*(1-o(k));%偏导
end
for j=1:Nh
tem=0.0;
for k=1:No
tem=tem+yitao(k)*W(j,k,bpj);
end
yitay(j)=tem*y(j)*(1-y(j));%偏导
end
for j=1:Nh%权值更新
for k=1:No
deltaW(j,k,bpj) = Learning_Rate*yitao(k)*y(j);
W(j,k,bpj) = W(j,k,bpj)+deltaW(j,k,bpj);
end
end
for i=1:NI
for j=1:Nh
deltaW0(i,j,bpj) = Learning_Rate*yitay(j)*x(i);
W0(i,j,bpj) = W0(i,j,bpj)+deltaW0(i,j,bpj);
end
end
end
jj=jj+1;
end
%BP训练结束
error = sum(mean(error2));
%误差是否达到精度
if error<Paim;
break;
end
Index = Index+1;
ERR = [ERR,error];
end
figure;
semilogy([1:10:Index-1],ERR(1:10:end),'linewidth',2);
grid on
xlabel('迭代次数');
xlabel('误差');
if Learning_Rate == 0.01;
save S11.mat Index ERR
end
if Learning_Rate == 0.05;
save S12.mat Index ERR
end
if Learning_Rate == 0.2;
save S13.mat Index ERR
end
if Learning_Rate == 0.5;
save S14.mat Index ERR
end
clc;
clear;
close all;
warning off;
RandStream.setDefaultStream(RandStream('mt19937ar','seed',1));
%加载数据
load australian.dat
data = australian;
%输入数据预处理
SET = [1:14];
for i = SET
P(:,i) = data(1:100,i)/max(data(1:100,i));
end
[P,minp,maxp] = premnmx(P);
T = data(1:end,end);
% P = rand(200,1);
% T = round(P);
Len = length(P);
%输入层节点
NI = size(P,2);
%输出层节点
No = 1;
%隐层节点
Nh = 14;
%最大迭代次数
Max_iteration = 3000;
%目标精度
Paim = 1e-3;
%学习率设定值
Learning_Rate = 0.02;
lemda = 0.3;
error = 0;
error2 = zeros(1,Len);
%BP1~4
KER = 4;%集成个数
W0 = rand(NI,Nh,KER);
deltaW0 = zeros(NI,Nh,KER);
dW0 = zeros(NI,Nh,KER);
W = rand(Nh,No,KER);
deltaW = zeros(Nh,No,KER);
dW = zeros(Nh,No,KER);
ERR = [];
Index = 1;
while(Index<=Max_iteration)
Index
jj=1;
error2 = zeros(Len,KER);
while(jj<=Len)
for k=1:No;
d(k)=T(jj);
end
for i=1:NI;
x(i)=P(jj,i);
end
%集成多个BP神经网络
for bpj = 1:KER
for j=1:Nh%BP前向
net=0;
for i=1:NI
net=net+x(i)*W0(i,j,bpj); %加权和∑X(i)V(i)
end
y(j)=1/(1+exp(-net));
end
for k=1:No
net=0;
for j=1:Nh
net=net+y(j)*W(j,k,bpj);
end
%输出值
o(k,bpj)=1/(1+exp(-net));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
errortmp = 0.0;
for k=1:No
errortmp=errortmp+(d(k)-o(k,bpj))^2;
end
errortmp = 0.5*errortmp/No;
errortmp2= 0.0;
%F(n) = 1/M x ∑f(i)
F = mean(o(k,:));
for k=1:No
p(k) =(o(k,bpj) - F) * (sum(o(k,:) - F) - (o(k,bpj) - F));
errortmp2 = errortmp2+lemda*p(k);
end
errortmp2 = errortmp2/No;
error2(jj,bpj)=errortmp + errortmp2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:No%BP反向计算
%偏导
yitao(k)=((d(k) - o(k,bpj)) + lemda*(o(k,bpj) - F))*o(k,bpj)*(1-o(k,bpj));
end
for j=1:Nh
tem=0.0;
for k=1:No
tem=tem+yitao(k)*W(j,k,bpj);
end
yitay(j)=tem*y(j)*(1-y(j));%偏导
end
for j=1:Nh%权值更新
for k=1:No
deltaW(j,k,bpj) = Learning_Rate*yitao(k)*y(j);
W(j,k,bpj) = W(j,k,bpj)+deltaW(j,k,bpj);
end
end
for i=1:NI
for j=1:Nh
deltaW0(i,j,bpj) = Learning_Rate*yitay(j)*x(i);
W0(i,j,bpj) = W0(i,j,bpj)+deltaW0(i,j,bpj);
end
end
end
jj=jj+1;
end
%BP训练结束
error = sum(mean(error2));
%误差是否达到精度
if error<Paim;
break;
end
Index = Index+1;
ERR = [ERR,error];
end
figure;
semilogy([1:10:Index-1],ERR(1:10:end),'linewidth',2);
grid on
xlabel('迭代次数');
xlabel('误差');
% axis([0,Index,1e-6,1]);
if Learning_Rate == 0.01;
save S21.mat Index ERR
end
if Learning_Rate == 0.05;
save S22.mat Index ERR
end
if Learning_Rate == 0.2;
save S23.mat Index ERR
end
if Learning_Rate == 0.5;
save S24.mat Index ERR
end
if lemda == 0.01;
save S21l.mat Index ERR
end
if lemda == 0.05;
save S22l.mat Index ERR
end
if lemda == 0.1;
save S23l.mat Index ERR
end
if lemda == 0.2;
save S24l.mat Index ERR
end
if lemda == 0.3;
save S25l.mat Index ERR
end
四、仿真结论分析
传统的4集成BP神经网络，不同的学习率下其仿真结论如下所示：
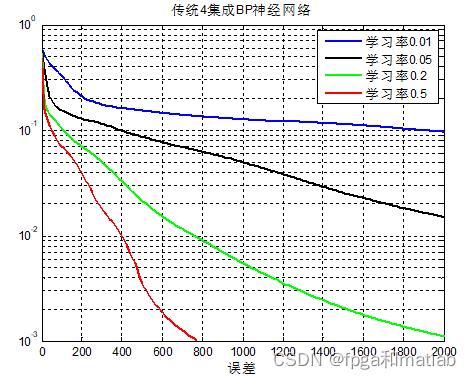
从上面的仿真结果可知，随着学习率的增加，BP神经网络的训练误差越来越小。这里，训练目标误差设定在0.001。
改进目标函数，其仿真结果如下图所示：
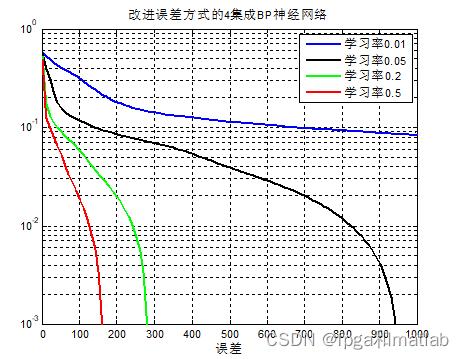
从上面的仿真结果可知，随着学习率的增加，BP神经网络的训练误差越来越小。 下面对比一下两种误差方式下的算法性能对比：
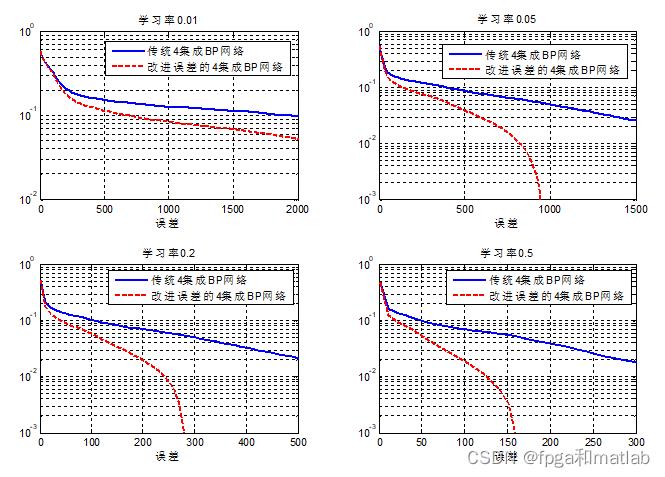
从上面的仿真对比可知，改进误差算法的BP神经网络，其网络的收敛速度更快，且能在相同训练次数的情况下，可以获得更高精度的预测结果。
A05-32
以上是关于基于负相关学习多神经网络集成的目标识别算法MATLAB仿真的主要内容，如果未能解决你的问题，请参考以下文章
基于FAST-RCNN深度学习的目标识别算法的MATLAB仿真