数据泛化是啥

Posted 2023-04-11

06-08-21] 来源： 作者： [字体：大 中 小]

黄建国
（合肥幼儿师范 现代教育技术中心 安徽 合肥 230011 ）
摘要 为了更有效的进行在线分类挖掘，提出了一种泛化算法。该算法结合了数据立方体技术和面向属性归纳方法中的泛化策略，有效降低了聚合运算的运算量，提高了运算效率，将数据库中的原始数据泛化成用户感兴趣的概念层次上的、聚合的、具有统计意义的元数据,为在线分类提供了良好的数据环境。
关键词 数据挖掘 数据泛化 数据立方体

1 引言
数据准备是KDD过程中一个很重要的过程，良好的数据准备过程能够为数据挖掘提供清洁、可靠、稳定的数据环境，以保证挖掘算法的有效实施。在线分类理想的数据环境应具备以下几个特点： （1）数据应包含丰富的属性信息，应具备可靠性和稳定性；
（2）数据的属性应具有对于分类任务的相关性。大多数的分类任务只与数据库中部分属性有关，多余的、无关的属性介入分类，常会减慢甚至错误引导分类过程，应此必须去掉无关属性。
（3）数据应具有高层数据信息，以发现清晰的、高层的、具有统计意义的分类规则。在本文的研究中，为了使数据环境达到上述要求，在数据准备阶段采用了数据泛化的策略，这个策略用概念层次作为背景，结合了OLAP技术与Jiawei Han等人的面向属性归纳的方法，明显提高了工作效率。
2 面向属性归纳中的基本泛化策略和算法
随着KDD研究的逐步深入， Jiawei Han等人提出了一种基于归纳的知识发现方法——面向属性的归纳方法[1][2][3]，这方法的特点是能够根据概念层次将低概念层的数据泛化到相应的高层次的概念层，以发现多层的或高层的规则。面向属性归纳方法是一种有效的、完整的知识发现算法，该算法将机器学习中示例学习方法与数据库的操作技术相结合[1]。算法的一个关键就是攀升属性所对应的概念层次树以泛化原始数据集的数据到用户感兴趣的概念层上，减少数据集的大小，从而降低知识发现过程的计算复杂度。面向属性归纳方法的进行，必须有两个前提：

（1）必须由用户提出明确的知识发现任务。在Jiawei Han等人的研究中，采用了一种类似SQL语句的知识发现语句DMQL[4]用来让用户定义发现任务，下面便是一个分类任务的语句描述：

要说明的是在本文的研究中采用了一个可视化的向导来引导用户定义发现任务，但为了文章描述方便，在本文的描述中，借用了DMQL来描述发现任务
（2）与发现任务相关的属性应有概念层次，如上文所述，数值型的概念层次可以自动提取，给定的概念层次可以用户的兴趣和发现任务的不同而进行动态调整。
在具备以上两个前提时，面向属性归纳采用了以下一些泛化策略。
● 泛化策略
策略1 在最小分解单位上泛化
一般而言，泛化都是在数据集的单个属性上进行的。因为单个属性常常是数据集中的最小分解单位。在最小分解单位上进行泛化，更能确定泛化过程中的细微变化，从而达到适度泛化的目的，避免过度泛化。
策略2 属性去除
如果一个属性在相关数据集中有大量不同的值，但是在其对应的概念层次树上，没有比该属性更高的概念层，则该属性将被从发现任务中去除。因为这样的属性是不可能被泛化到更高的概念层的，这是符合示例学习理论的。
策略3 概念树攀升
如果一个属性在概念层次树上有更高层次的概念，那么在泛化后的数据集中将所有记录的该属性值以高层次的属性值替代。
策略4 增加属性CNT
作为策略3的执行结果，必然会有许多不同的纪录由于属性值完全相同而合并成一条纪录。为了反应这一变化，引入属性CNT来纪录最初的表中不同纪录被概括成泛化表中相同纪录的个数。属性CNT在泛化的过程中保存了最初的计数，该值在知识发现的过程中起到了重要作用。
策略5 设立阈值
利用策略2中的CNT可以定义规则的正确率P，P=（符合规则的CNT值）/（符合规则左边属性条件的CNT值）。这样可以定义一阈值L用于取舍规则，若P>L则规则有效，否则丢弃该规则。另外，对一个属性A而言，为了将数据集概括到一定层次，必须沿着A的概念层次向上爬行几次。为了控制这个过程，有必要设置一归纳阈值，若A的取值个数达到这一阈值，则无需进一步概括，否则必须进行进一步的概括。除此之外，我们还可以对泛化表设置一个归纳阈值，如果泛化表的记录树大于该归纳阈值，则进行进一步的泛化直到满足这个归纳阈值为止。以上策略可以总结成算法如下：
算法1 (基本泛化算法)
输入条件：1.一个关系数据集，2 一个学习任务，3 一套相关属性的概念层次，4 每个属性归纳阈值t[i](i=1 to n，于属性相对应)、一个泛化表归纳阈值t2。
输出：一个用户期望的泛化后的数据集。
步骤：本算法可以分为两大步：
Step1. 根据用户提交的学习任务，从原始的关系数据集中收集与任务相关的属性与数据。生成初始泛化集GR；
Step2. 运行基本的泛化算法产生泛化数据集。
注意，step2可以细化成如下算法：
begin
for GR中的每一个属性Ai do
begin
while Ai的不同值的数目>t[i] do
begin
if Ai在概念层次中有高层次的概念 THEN
将Ai的所有值以高层次的概念值取代
else
在GR中移去Ai;
合并同样的记录；
end;
end；
while GR中的记录数>t2 do
begin
选择泛化属性进一步泛化；
合并相同的记录。
end;
end.
3 基于数据立方体的泛化算法
上述泛化算法是针对关系表的，其生成的结果也是关系数据表。对泛化后关系数据表进行分类规则挖掘时仍要进行大量的聚合运算，如计数、求和等。有没有办法降低聚合运算的运算量呢？有，那就是数据立方体。我们知道数据立方体的方格内存放的就是一些聚合值，而且对数据立方体进行聚合运算，其效率远高于对关系数据库进行聚合运算。基于此，本文提出了一种基于数据立方体的算法。
● 基于数据立方体的泛化算法
本算法共分为四步：第一步，初始化。首先，根据用户提出的发现任务，收集相关数据。（这里需说明的一点是此处用户提出的发现任务的相关属性实际上是一个维的概念，它可能对应于数据库中一个或几个有层次关系的实际属性。在下面的例子中我们将看到这一点。）然后确定每维的概念层次（自动提取数值型概念层次或动态调整已有概念层次）。第二步，构造基本立方体（Basecube）。这一步中首先根据数据库的数据分布特性（对于离散属性确定不同值的个数，连续值则确定数值间的最小间隔）确定每维的最初泛化层次，然后进行聚合计算来构造基本立方体。第三步，按照基本泛化策略对每维进行泛化造作，以确定每维理想的泛化层次。第四步，在新的泛化层次上对Basecube进行再计算，以构造最终的泛化立方体Primecube。这一步中将大量使用数据立方体的操作。该算法的形式描述如下：
算法2 基于数据立方体的泛化算法
输入：
1 一个待挖掘的关系数据集；
2 一个学习任务；
3 一个概念层次集合Gen(Ai)，Ai是任意维；
4 Ti，任意维Ai的泛化阈值。
输出：一个最终泛化的数据立方体。
方法：
⑴ 始化：
① 根据用户的学习任务，确定每一维对应的属性，并从初始关系数据集中收集相关的数据。
② for 每一维Ai do
begin
if Ai是数值型 and Ai没有概念层次 then 自动生成概念层次（算法2.1）
else 动态调整概念层次以适应当前学习任务；
end;
⑵ 造Basecube：
① 对于每一维的属性计算其在数据库中对应的不同值的个数，如果是数值型则计算数值间的最小间隔，根据不同值的个数或最小间隔确定每一维的最初泛化层次。
② 按最初泛化层次确定每维的维成员，并进行COUNT，SUM等聚合运算。用文[26]中算法构造基本立方体。
⑶ 确定每维的泛化层次。
① 根据每一维的泛化阈值，进行基本泛化（算法2.5）找到最终理想的层次Li。
② 找出每一维Ai的映射<v,v’>，其中v是维成员值，v’是v在泛化层上对应的概念值。
⑷ 构造Primecube。
① 将Basecube的维成员v替换成v’;
② 对Basecube进行数据立方体操作，构造Primecube。
本算法中，第一步的时间复杂度主要依赖于特定数据库的操作和提取或调整概念层次的算法的效率。第二步的主要操作在于立方体的构造上，复杂度为 。第三步和第四步都只对基本立方体进行一次扫描，加上计算量，复杂度也为 。所以本算法中二到四步总的时间复杂度应为 。
下面以一个例子来进一步描述该算法。

例1：从网上下了一个数据库CITYDATA，该数据库记录了美国地区城市的情况。其中有三个表，如下：

表1 CityLocation 记录城市所在地

表2 LaborIncome 记录城市人员的收入

表3 记录犯罪率与教育程度

我们有一个初始概念层次US_LOCATION：

…

现在我们要对数据库进行如下任务的发现：

CLASSIFY CITYDATA
ACCORDING TO UNEMPLOYMENT_RATE
IN RELEVANCE TO US_LOCATION，FAMILY_INCOME，POVERTY_PCT，
CRIME_RATE，BACHELOR_PCT
FROM LABORINCOME，CRIMEEDUCATION
注意到该发现任务中的维US_LOCATION对应着几个有层次关系的数据库属性：area-name→county→state→region→big region→country，这些属性在概念层次Us location中都对应着相应的层次。每一维的阈值为5。
根据算法，我们首先作初始化，对family income，poverty pct，crime_rate，bachelor_pct由于它们是数值型的属性，所以概念层次可以自动提取出来，下面便是自动提取出来的概念层次：
运行算法二、三、四步，得到六维的基本立方体和泛化立方体，为方便起见本文给出其中三维的立方体图。

最后的泛化结果放在了表4。注意到cityid的属性已被移去。

表4 最后的泛化结果
4 结束语
数据泛化在线分类研究中占有重要地位，它是在线分类规则挖掘算法的基础。在线分类任务的一个重要特征就是数据量庞大，且数据中含有一定量的异常信息，这样的数据是不适合直接分类的。通过数据泛化，可以将数据整理、清洁，为分类提供较好的数据环境。另外数据泛化采用了概念层次技术，可以发现高层的分类规则，从而使分类结果更易理解。
本文结合基本的面向属性归纳技术，提出了一种数据立方体的数据泛化算法，给在线分类提供了较好的数据预处理技术。

参考文献
[1] Han J, Fu Y. Exploration of the power of attribute-oriented induction in data mining. In: Fayyad U M et al eds. Advances in Knowledge Discover and Data Mining. Cambridge: AAAI/MIT Press, 1996. 399～421
[2] J. Han, Y. Cai, and N. Cercone. Knowledge discovery in databases: An attribute_Oriented approach. In Proc. 18th Int. Conf. Very Large Data Bases, pages 547--559, Vancouver, Canada, August 1992.
[3] Cheung D W, Fu A W C, Han J. Knowledge discovery in databases: a rule based attribute oriented approach. In: Zbigniew R ed. Methodologies for Intelligent systems: 8th International Symposium. Berlin: Springer-Verlag, 1994. 164～173
[4] Han, J., Chiang, J., Chee, S., Chen, J., Chen, Q., Cheng, S., Gong, W., Kamber, M., Liu, G., Koperski, K., Lu, Y., Stefanovic, N., Winstone, L., Xia, B., Zaiane, O. R., Zhang, S. & Zhu, H. (1997), DBMiner: A system for data mining in relational databases and data warehouses, in `Proc. CASCON'97: Meeting of Minds', Toronto, Canada, pp. 249--260.

作者简介：
黄建国(1974年10月-- ) ，男，安徽省合肥市人，合肥幼儿师范学校讲师，中国科技大学计算机应用工程硕士。 参考技术A 数据泛化是一个从相对低层概念到更高层概念且对数据库中与任务相关的大量数据进行抽象概述的一个分析过程。

在线分类理想的数据环境应具备以下几个特点： （1）数据应包含丰富的属性信息，应具备可靠性和稳定性；
（2）数据的属性应具有对于分类任务的相关性。大多数的分类任务只与数据库中部分属性有关，多余的、无关的属性介入分类，常会减慢甚至错误引导分类过程，应此必须去掉无关属性。
（3）数据应具有高层数据信息，以发现清晰的、高层的、具有统计意义的分类规则。在本文的研究中，为了使数据环境达到上述要求，在数据准备阶段采用了数据泛化的策略，这个策略用概念层次作为背景，结合了OLAP技术与Jiawei Han等人的面向属性归纳的方法，明显提高了工作效率。

K-NN聚类算法的良好泛化，可用于数据简化

图：pixabay

原文来源：atasciencecentral

「机器人圈」编译：嗯~阿童木呀、多啦A亮

在本文中我将描述一种有趣且直观的聚类算法（可以用于数据简化），相较于传统的分类器，它具有以下优势：

•对异常值和错误数据具有更强的鲁棒性。

•执行速度更快。

•泛化了一些知名的算法。

对于本文所涉及的内容：

1.即使你对K-NN不是非常了解也没关系，当然，如果你想了解更多信息，请点击此处链接（）。

2.你不需要具备统计学的背景知识。

接下来，我们用简单明了、通俗易通的语言来描述这个新算法及其各个组成部分。

通用框架

我们将要处理的是一个监督学习问题，更具体地说，是聚类（也称为监督分类）。特别地，我们要为一个不属于训练集的新观察值分配一个类标签。相较于检查个别点（最近的邻值），并使用多数（投票）规则，根据最近的邻居数将新的观察值分配给一个群集，我们的方法是检查点的簇（簇s），并将关注点放在放在最近的簇中而不是最近的点。

簇和簇密度

此处所考虑的簇是由圆（二维）或球体（三维）进行定义的。在最基本的版本中，我们为每个集群提供一个簇，而簇被定义为最小的圆，它包含了上述集群中点的预定比例p。如果聚类能够很好得进行分离，我们甚至可以使用p = 1。我们将簇的密度定义为单位面积上的点数。一般来说，我们想要建立的是具有高密度的簇。

理想情况下，我们希望训练集中的每个集群都能够被少量（可能是轻微重叠）的簇所覆盖，且每一个都具有高密度。此外，作为通用规则，训练集中的一个点只能属于一个簇，（理想情况下）只能属于一个集群。但是，与两个簇相关联的圆是允许重叠的。

分类规则，计算复杂性，内存需求

一旦我们为每个集群建立了一组簇集合，分类规则就很简单了。构建这些簇是复杂的预处理步骤，但是正如上一所描述的那样，我们只需要进行粗略的近似就可以了。分类规则如下：

•1-NC算法：将新的观察值分配给最接近最近簇的集群。

•K-NC算法：在最接近问题中观察值的K个簇（多数票选）中，将新的观察值分配给具有最多个簇数量的集群。

需要注意的是，如果簇是由单个点组成的，则K-NN和K-NC算法是相同的。还要注意的是，计算点和簇之间的距离是很直截了当的，因为簇是圆形的。你只需要知道上述中所讨论的圆的圆心和半径就可以了。

最后，为了将一个新的观察值平分配到一个集群中，只需要检查所有的簇，而不是所有的点。因此，K-NC算法要比K-NN快v倍，其中v是训练集中的点数除以所有集群的簇数。实际上，我们所拥有的簇数要远小于训练集中的点数，所以在处理非常大的训练集时，v可能很大。特别是簇之间没有太多的重叠的时候，更是如此。

简而言之，这些簇整合了训练集数据：一旦这些簇经过计算之后，我们便可以丢弃所有的数据，并且只保留簇（包括它们的中心、半径、密度和集群标签）。这也节省了大量的内存，本身也可以用作数据简化技术。

簇构建和最小圆问题

在构建簇系统时，这个概念可被证明可能是有效的。最小圆问题（点击查看详细信息）涵盖的是计算包含给定区域中所有点的最小圆。如下图所示。

 

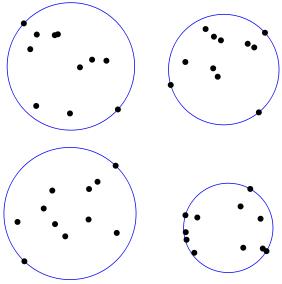
基于最小圆问题计算的簇

人们会认为这样的簇是否具有最大的密度，一种理想的性能。现在有几种非常有效的算法可以解决这个问题。有些甚至允许你为每一个点添加一个权重。

集群产生的重力场

你可以选择跳过本章节，如果你有兴趣来进一步了解如何改进K-NC算法，以及改进诸如K-NN等标准算法，那么你就该好好阅读该章节了。另外，它强调了一个事实，即在计算点之间的平均距离时，相较于原始距离，距离的平方可能是一个更好的衡量指标（从建模的角度来看）。这就像许多物理定律种所涉及的“距离”，往往是两个对象之间距离的平方，而不是距离本身。换句话说，你可以按照引力定律的思维方式来看待一个分类问题：（在分类背景中）哪个集群将“吸引”一个新的观察值呢？就对应于（天体物理学背景中）哪个天体将吸引和吸附一个流星体。你会认为在这两种情况下，类似的定理都是适用的。

对于每个点x（通常指的是我们要分类的新点）和集群G，潜在V（x，G）定义如下：

 

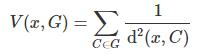
其中总和超过了G中的所有簇。其实一个更好的定义可能是仅在G中的k个最邻近的簇中取总和，以获得预定义的k值。潜在的分类规则是将点x分配给最大化v（x，G）的集群G。

最后的改进工作包括在上述总和中为每一项添加一个权重：权重是相应簇的密度。请注意，如果簇（它们所代表的圆）有着显著的重叠情况，则应在潜在的定义V中加以解决。通常情况下，训练集点只能属于一个簇，（理想情况下）只能属于一个集群。

创建有效的簇系统

这个数据预处理步骤是一个较为复杂的步骤。然而，易于获取的近似解决方案实施效果非常好。毕竟，即使每个点都是一个簇（K-NN为特殊情况），我们也能得到非常理想的结果。

几种不同的可行性方法：

•从每个训练集点的一个簇开始，并迭代地合并这些簇。

•基于上述的最小圆问题，从每个集群的一个簇开始，然后对其进行收缩并移动中心，直到它包含训练集点的比例p，且上述集群中簇的密度达到最大值（或者足够接近最大值）。接下来对上述集群中剩余的点重复此操作。假设每个集群中都有一个包含至少30%点数的圆形内核，那么可以选择p=30%。

•在每个群集中从预先指定数量的随机簇（随机半径、随机圆心、可能与训练集中随机选择的点相对应）开始。每次调整一个簇的圆心和半径，以优化一些下面所述的与密度相关的标准。此外，如果随着时间的推进，使用生成和消亡过程来淘汰一些簇，并不断创建新的，也是一个不错的方法。

这些方法的目的是获得尽可能少的簇，能够覆盖整个训练集而不产生过多的重叠。每个簇必须具有高密度，且须包含超过（例如）上述集群中训练集点数的1％。我们可以增加一个限制条件：每个簇必须至少含有两个点。

 

非圆形簇

 

其实，测试簇的形状是否重要也是一件很有意思的事情。只要我们有足够多的簇，形状可能就没那么重要了（这一点应该经过验证），因此圆形—由于它在测量簇和点之间的距离时能够极大地简化计算—可以说是最为理想的选择。请注意，如果一个点在一个簇内部（在其圆内），则簇和该点之间的距离为零。我们应该测试这个规则是否对异常值或错误数据具有更强的鲁棒性。

源代码

我希望在不久之后可以提供一段关于K-NC分类器的代码，特别是建立一个运作良好的簇系统。而且很明显的一点是，如果是基于它是一个泛化（也可以用于数据简化）的意义上来讲，这种算法要比K-NN好得多，但是也可以去尝试测试什么样的簇（小或大）能够提供基于交叉验证的最佳结果，且会有多大的改进程度，应该是很有趣的。

同时，我鼓励读者设计一个实现，也许在Python中。这将是一个伟大的数据科学项目。我将发布并提供这些解决方案，为作者提供支持（例如，在LinkedIn上），并向他/她发送我的Wiley book（）的签名副本。

潜在的增强、数据简化和结论

对我们的方法的潜在改进包括：

•利用密度和邻近性，在将一个新的观察值分配给一个集群时，将重点放在更为密集的簇中。

•允许训练集点属于同一集群内的多个簇。

•允许训练集点属于多个集群。

•测试由最近邻居组成的簇。

•减少簇之间的重叠。

此外，我们需要测试这个新算法，并根据创建簇的方式来查看它在什么时候能够运行得更好。假设在每种情况下使用不同的K值，K-NC是不是就相当于K-NN？即使它们是等价的，K-NC有一个很大的好处就是：它可以用于数据简化，而且与传统的数据简化技术是不一样的。诸如PCA这样的传统数据简化技术尝试将数据集投影到具有较低维度的空间上。由K-NC生成的簇结构是一种数据简化技术的结果，它不执行降维或投影，而是在相同的原始空间中执行类似于数据精简或数据压缩或熵减少的方法。

另一个好处是，得益于K-NC在构建簇结构时的预处理步骤，其运行速度要比K-NN快得多。它也更直观，主要是因为它基于直观的概念，每个集群由子集群簇组成。它确实与代表集群结构的随机点过程的模型拟合相类似，例如奈曼-斯科特（Neyman-Scott）集群过程。

最后，在许多情况下，改进分类器的一种方法是通过重新缩放或转换数据，例如使用对数刻度。大多数分类器是依赖于尺度的，我们正在开发不断扩展的尺度分类器，就像我们引入（scale-invariant variance）一样。

想要了解更多详细内容及相关学科知识，请点击此处链接：。

 

欢迎加入

关注“机器人圈”后不要忘记置顶哟

↓↓↓点击阅读原文查看中国人工智能产业创新联盟手册