K-NN聚类算法的良好泛化，可用于数据简化

Posted 2021-04-09 雷克世界

图：pixabay

原文来源：atasciencecentral

「机器人圈」编译：嗯~阿童木呀、多啦A亮

在本文中我将描述一种有趣且直观的聚类算法（可以用于数据简化），相较于传统的分类器，它具有以下优势：

•对异常值和错误数据具有更强的鲁棒性。

•执行速度更快。

•泛化了一些知名的算法。

对于本文所涉及的内容：

1.即使你对K-NN不是非常了解也没关系，当然，如果你想了解更多信息，请点击此处链接（）。

2.你不需要具备统计学的背景知识。

接下来，我们用简单明了、通俗易通的语言来描述这个新算法及其各个组成部分。

通用框架

我们将要处理的是一个监督学习问题，更具体地说，是聚类（也称为监督分类）。特别地，我们要为一个不属于训练集的新观察值分配一个类标签。相较于检查个别点（最近的邻值），并使用多数（投票）规则，根据最近的邻居数将新的观察值分配给一个群集，我们的方法是检查点的簇（簇s），并将关注点放在放在最近的簇中而不是最近的点。

簇和簇密度

此处所考虑的簇是由圆（二维）或球体（三维）进行定义的。在最基本的版本中，我们为每个集群提供一个簇，而簇被定义为最小的圆，它包含了上述集群中点的预定比例p。如果聚类能够很好得进行分离，我们甚至可以使用p = 1。我们将簇的密度定义为单位面积上的点数。一般来说，我们想要建立的是具有高密度的簇。

理想情况下，我们希望训练集中的每个集群都能够被少量（可能是轻微重叠）的簇所覆盖，且每一个都具有高密度。此外，作为通用规则，训练集中的一个点只能属于一个簇，（理想情况下）只能属于一个集群。但是，与两个簇相关联的圆是允许重叠的。

分类规则，计算复杂性，内存需求

一旦我们为每个集群建立了一组簇集合，分类规则就很简单了。构建这些簇是复杂的预处理步骤，但是正如上一所描述的那样，我们只需要进行粗略的近似就可以了。分类规则如下：

•1-NC算法：将新的观察值分配给最接近最近簇的集群。

•K-NC算法：在最接近问题中观察值的K个簇（多数票选）中，将新的观察值分配给具有最多个簇数量的集群。

需要注意的是，如果簇是由单个点组成的，则K-NN和K-NC算法是相同的。还要注意的是，计算点和簇之间的距离是很直截了当的，因为簇是圆形的。你只需要知道上述中所讨论的圆的圆心和半径就可以了。

最后，为了将一个新的观察值平分配到一个集群中，只需要检查所有的簇，而不是所有的点。因此，K-NC算法要比K-NN快v倍，其中v是训练集中的点数除以所有集群的簇数。实际上，我们所拥有的簇数要远小于训练集中的点数，所以在处理非常大的训练集时，v可能很大。特别是簇之间没有太多的重叠的时候，更是如此。

简而言之，这些簇整合了训练集数据：一旦这些簇经过计算之后，我们便可以丢弃所有的数据，并且只保留簇（包括它们的中心、半径、密度和集群标签）。这也节省了大量的内存，本身也可以用作数据简化技术。

簇构建和最小圆问题

在构建簇系统时，这个概念可被证明可能是有效的。最小圆问题（点击查看详细信息）涵盖的是计算包含给定区域中所有点的最小圆。如下图所示。

 

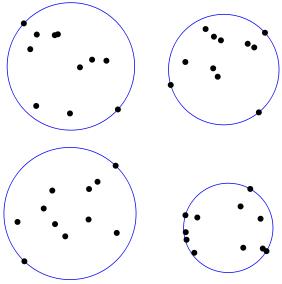
基于最小圆问题计算的簇

人们会认为这样的簇是否具有最大的密度，一种理想的性能。现在有几种非常有效的算法可以解决这个问题。有些甚至允许你为每一个点添加一个权重。

集群产生的重力场

你可以选择跳过本章节，如果你有兴趣来进一步了解如何改进K-NC算法，以及改进诸如K-NN等标准算法，那么你就该好好阅读该章节了。另外，它强调了一个事实，即在计算点之间的平均距离时，相较于原始距离，距离的平方可能是一个更好的衡量指标（从建模的角度来看）。这就像许多物理定律种所涉及的“距离”，往往是两个对象之间距离的平方，而不是距离本身。换句话说，你可以按照引力定律的思维方式来看待一个分类问题：（在分类背景中）哪个集群将“吸引”一个新的观察值呢？就对应于（天体物理学背景中）哪个天体将吸引和吸附一个流星体。你会认为在这两种情况下，类似的定理都是适用的。

对于每个点x（通常指的是我们要分类的新点）和集群G，潜在V（x，G）定义如下：

 

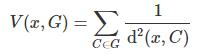
其中总和超过了G中的所有簇。其实一个更好的定义可能是仅在G中的k个最邻近的簇中取总和，以获得预定义的k值。潜在的分类规则是将点x分配给最大化v（x，G）的集群G。

最后的改进工作包括在上述总和中为每一项添加一个权重：权重是相应簇的密度。请注意，如果簇（它们所代表的圆）有着显著的重叠情况，则应在潜在的定义V中加以解决。通常情况下，训练集点只能属于一个簇，（理想情况下）只能属于一个集群。

创建有效的簇系统

这个数据预处理步骤是一个较为复杂的步骤。然而，易于获取的近似解决方案实施效果非常好。毕竟，即使每个点都是一个簇（K-NN为特殊情况），我们也能得到非常理想的结果。

几种不同的可行性方法：

•从每个训练集点的一个簇开始，并迭代地合并这些簇。

•基于上述的最小圆问题，从每个集群的一个簇开始，然后对其进行收缩并移动中心，直到它包含训练集点的比例p，且上述集群中簇的密度达到最大值（或者足够接近最大值）。接下来对上述集群中剩余的点重复此操作。假设每个集群中都有一个包含至少30%点数的圆形内核，那么可以选择p=30%。

•在每个群集中从预先指定数量的随机簇（随机半径、随机圆心、可能与训练集中随机选择的点相对应）开始。每次调整一个簇的圆心和半径，以优化一些下面所述的与密度相关的标准。此外，如果随着时间的推进，使用生成和消亡过程来淘汰一些簇，并不断创建新的，也是一个不错的方法。

这些方法的目的是获得尽可能少的簇，能够覆盖整个训练集而不产生过多的重叠。每个簇必须具有高密度，且须包含超过（例如）上述集群中训练集点数的1％。我们可以增加一个限制条件：每个簇必须至少含有两个点。

 

非圆形簇

 

其实，测试簇的形状是否重要也是一件很有意思的事情。只要我们有足够多的簇，形状可能就没那么重要了（这一点应该经过验证），因此圆形—由于它在测量簇和点之间的距离时能够极大地简化计算—可以说是最为理想的选择。请注意，如果一个点在一个簇内部（在其圆内），则簇和该点之间的距离为零。我们应该测试这个规则是否对异常值或错误数据具有更强的鲁棒性。

源代码

我希望在不久之后可以提供一段关于K-NC分类器的代码，特别是建立一个运作良好的簇系统。而且很明显的一点是，如果是基于它是一个泛化（也可以用于数据简化）的意义上来讲，这种算法要比K-NN好得多，但是也可以去尝试测试什么样的簇（小或大）能够提供基于交叉验证的最佳结果，且会有多大的改进程度，应该是很有趣的。

同时，我鼓励读者设计一个实现，也许在Python中。这将是一个伟大的数据科学项目。我将发布并提供这些解决方案，为作者提供支持（例如，在LinkedIn上），并向他/她发送我的Wiley book（）的签名副本。

潜在的增强、数据简化和结论

对我们的方法的潜在改进包括：

•利用密度和邻近性，在将一个新的观察值分配给一个集群时，将重点放在更为密集的簇中。

•允许训练集点属于同一集群内的多个簇。

•允许训练集点属于多个集群。

•测试由最近邻居组成的簇。

•减少簇之间的重叠。

此外，我们需要测试这个新算法，并根据创建簇的方式来查看它在什么时候能够运行得更好。假设在每种情况下使用不同的K值，K-NC是不是就相当于K-NN？即使它们是等价的，K-NC有一个很大的好处就是：它可以用于数据简化，而且与传统的数据简化技术是不一样的。诸如PCA这样的传统数据简化技术尝试将数据集投影到具有较低维度的空间上。由K-NC生成的簇结构是一种数据简化技术的结果，它不执行降维或投影，而是在相同的原始空间中执行类似于数据精简或数据压缩或熵减少的方法。

另一个好处是，得益于K-NC在构建簇结构时的预处理步骤，其运行速度要比K-NN快得多。它也更直观，主要是因为它基于直观的概念，每个集群由子集群簇组成。它确实与代表集群结构的随机点过程的模型拟合相类似，例如奈曼-斯科特（Neyman-Scott）集群过程。

最后，在许多情况下，改进分类器的一种方法是通过重新缩放或转换数据，例如使用对数刻度。大多数分类器是依赖于尺度的，我们正在开发不断扩展的尺度分类器，就像我们引入（scale-invariant variance）一样。

想要了解更多详细内容及相关学科知识，请点击此处链接：。

 

欢迎加入

关注“机器人圈”后不要忘记置顶哟

↓↓↓点击阅读原文查看中国人工智能产业创新联盟手册