递归：汉诺塔问题

Posted 2022-08-22 我家大宝最可爱

汉诺塔问题

原问题是把N个圆盘由A移动到C，子问题可以变为把N-1个圆盘由A移动到B，然后在把这个N-1个圆盘移动到C。从下图可以看到共调用了两次子问题

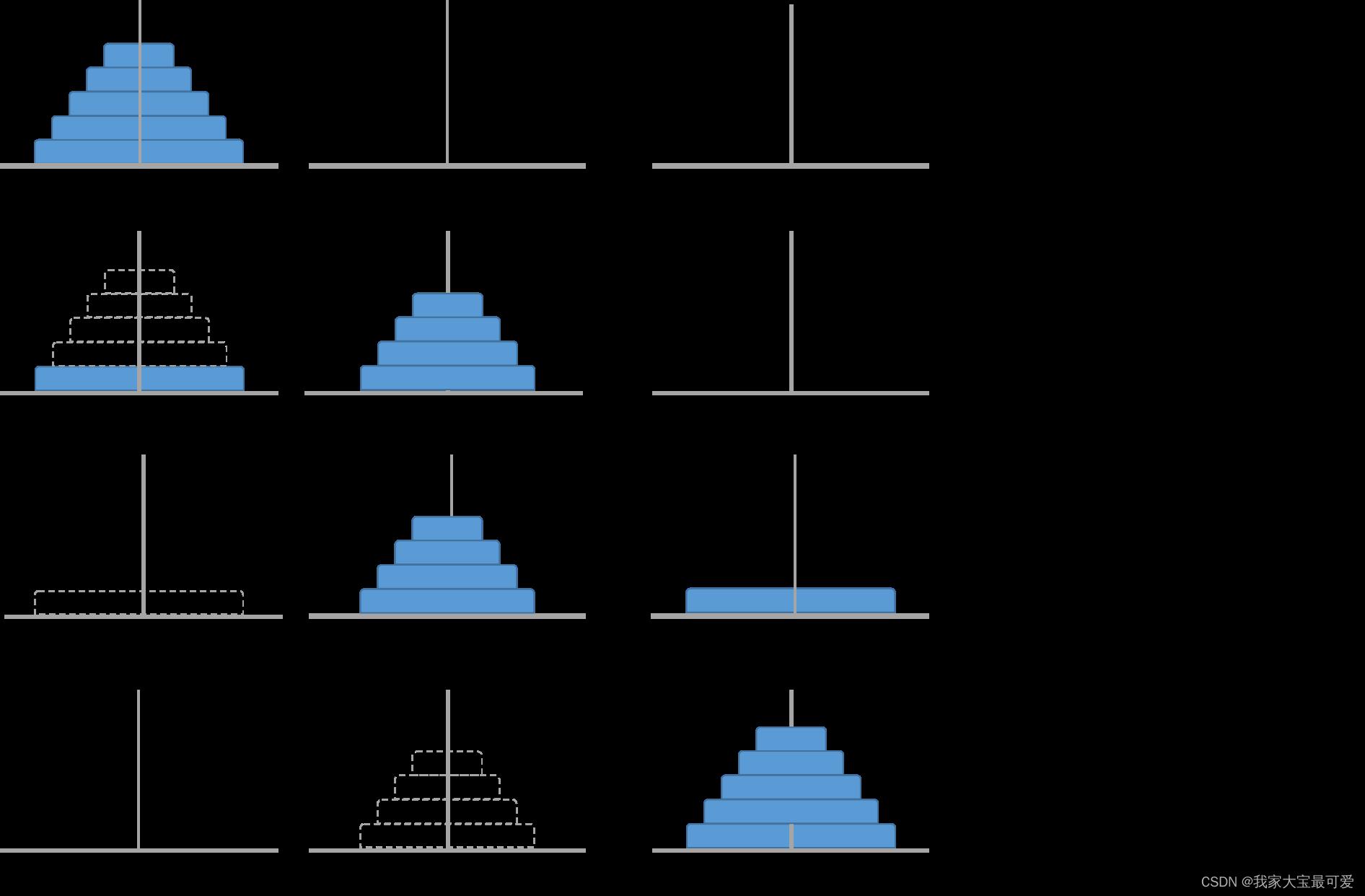
最终的代码也非常的简单

class Solution:
    def hanota(self, A: List[int], B: List[int], C: List[int]) -> None:
        """
        Do not return anything, modify C in-place instead.
        """

        def move(n,A,B,C): # 原问题
            if n == 1:
                C.append(A.pop())
                return

            move(n-1, A, C, B) # 子问题
            C.append(A.pop()) # 逻辑
            move(n-1, B, A, C) # 子问题
        
        n = len(A)
        move(n,A,B,C)

还有一种打印版本的汉诺塔

def move(n,A,B,C):
    if n == 1:
        print('->'.format(A,C))
        return
    
    move(n-1,A,C,B)
    print('->'.format(A,C))
    move(n-1,B,A,C)

move(3,'A','B','C')