算法——汉诺塔问题(递归典型)
Posted czc1999
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法——汉诺塔问题(递归典型)相关的知识,希望对你有一定的参考价值。
汉诺塔
汉诺塔是一个发源于印度的益智游戏,也叫河内塔。相传它源于印度神话中的大梵天创造的三个金刚柱,一根柱子上叠着上下从小到大64个黄金圆盘。大梵天命令婆罗门将这些圆盘按从小到大的顺序移动到另一根柱子上,其中大圆盘不能放在小圆盘上面。当这64个圆盘移动完的时候,世界就将毁灭。

算法分析:
一阶汉诺塔的移动,显而易见,从 A->C
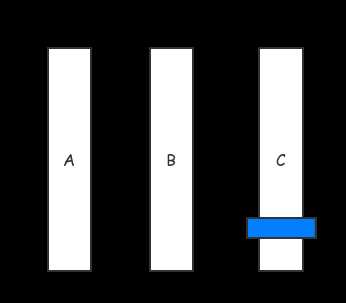
然后,我们可以探讨二阶与一阶的联系:
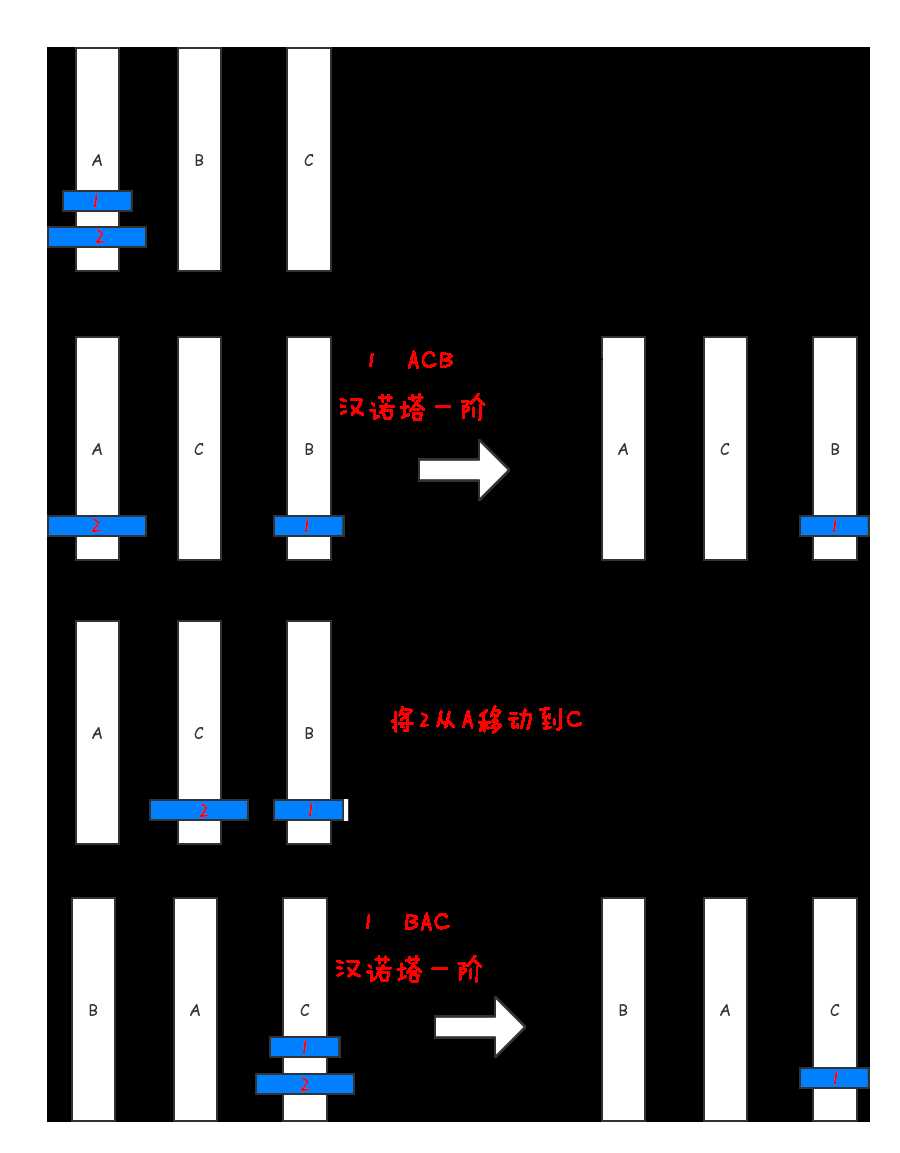
不光是对于二阶,其实N阶汉诺塔相当于执行了三大步骤:
1.在ACB的顺序下执行了(N-1)阶汉诺塔的移法
2.从A->C移动了第N个盘(最大的)
3.在BAC的顺序下执行了(N-1)阶汉诺塔的移法
分析清楚,那么代码就很简单了。
void process(int n,string A,string B,string C) { if (n == 1) { cout << "move from 1 " << A << " to " << C << endl; return; } process(n - 1, A, C, B); cout << "move from " <<n<<" "<< A << " to " << C << endl; process(n - 1, B, A, C); }
复杂度分析:
根据递归,我们很容易得到一个等式,T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1) + 1 ,时间复杂度是O(2^n - 1),证明也很容易。
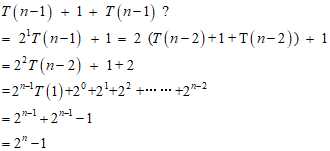
以上是关于算法——汉诺塔问题(递归典型)的主要内容,如果未能解决你的问题,请参考以下文章