STARKs and STARK VM: Proofs of Computational Integrity

Posted 2022-08-16 mutourend

1. 引言

所谓Proofs of Computational Integrity，是指：

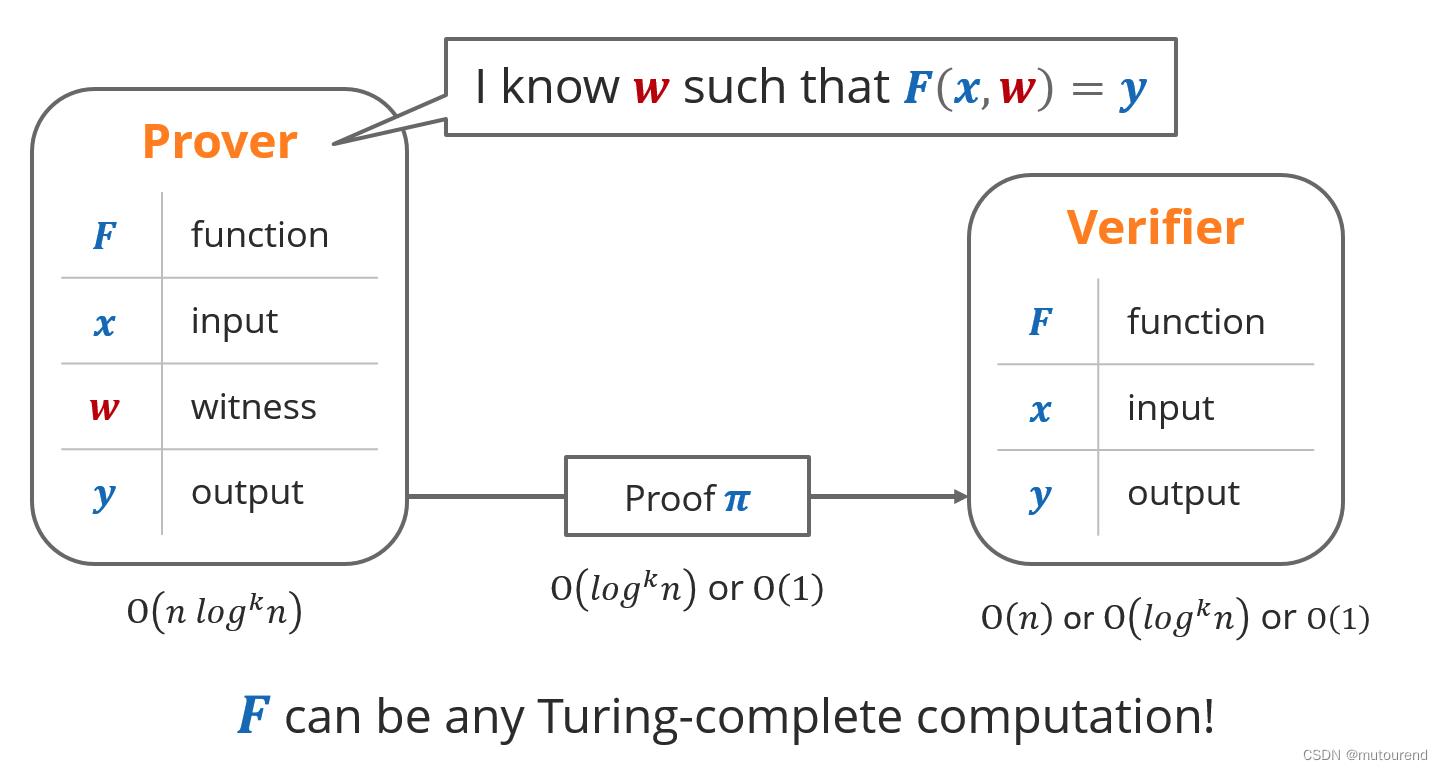
2. 现有ZKP证明系统

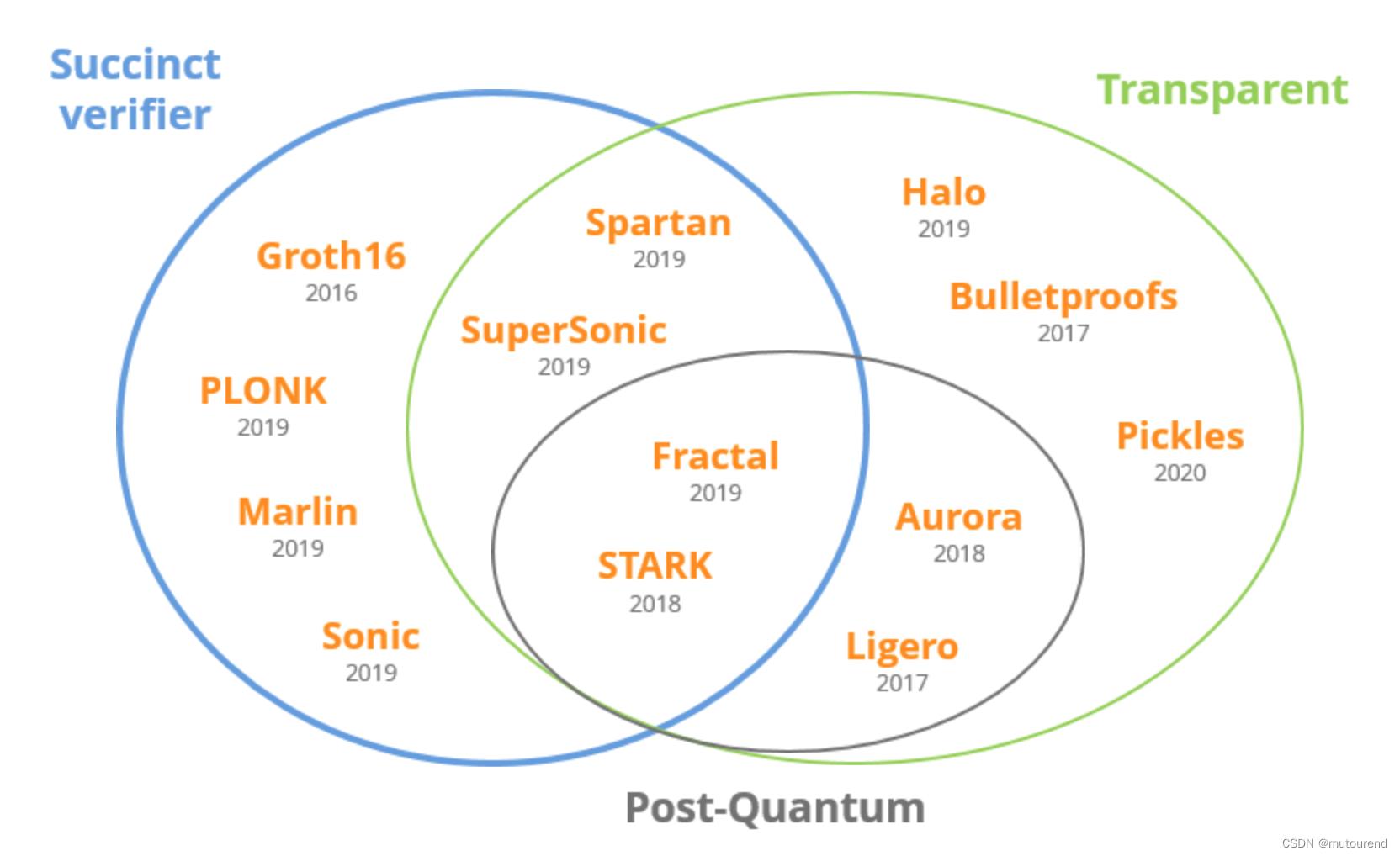
现有的ZKP证明系统主要有：

• 1）具有Succinct Verifier的ZKP系统有：
  • 1.1）Groth16：2016年
  • 1.2）STARK：2018年
  • 1.3）PLONK：2019年
  • 1.4）Marlin：2019年
  • 1.5）Sonic：2019年
  • 1.6）SuperSonic：2019年
  • 1.7）Spartan：2019年
  • 1.8）Fractal：2019年
• 2）Transparent无需可信设置的ZKP系统有：
  • 2.1）Bulletproofs：2017年
  • 2.2）Ligero：2017年
  • 2.3）STARK：2018年
  • 2.4）Aurora：2018年
  • 2.5）Spartan：2019年
  • 2.6）SuperSonic：2019年
  • 2.7）Fractal：2019年
  • 2.8）Halo：2019年
  • 2.9）Pickles：2020年
• 3）Post-Quantum抗量子ZKP系统有：
  • 3.1）Ligero：2017年
  • 3.2）Aurora：2018年
  • 3.3）STARK：2018年
  • 3.4）Fractal：2019年

这些ZKP系统从是否需要可信设置、Proof size、Prover speed、Verifier speed、密码学安全假设 维度对比如下：

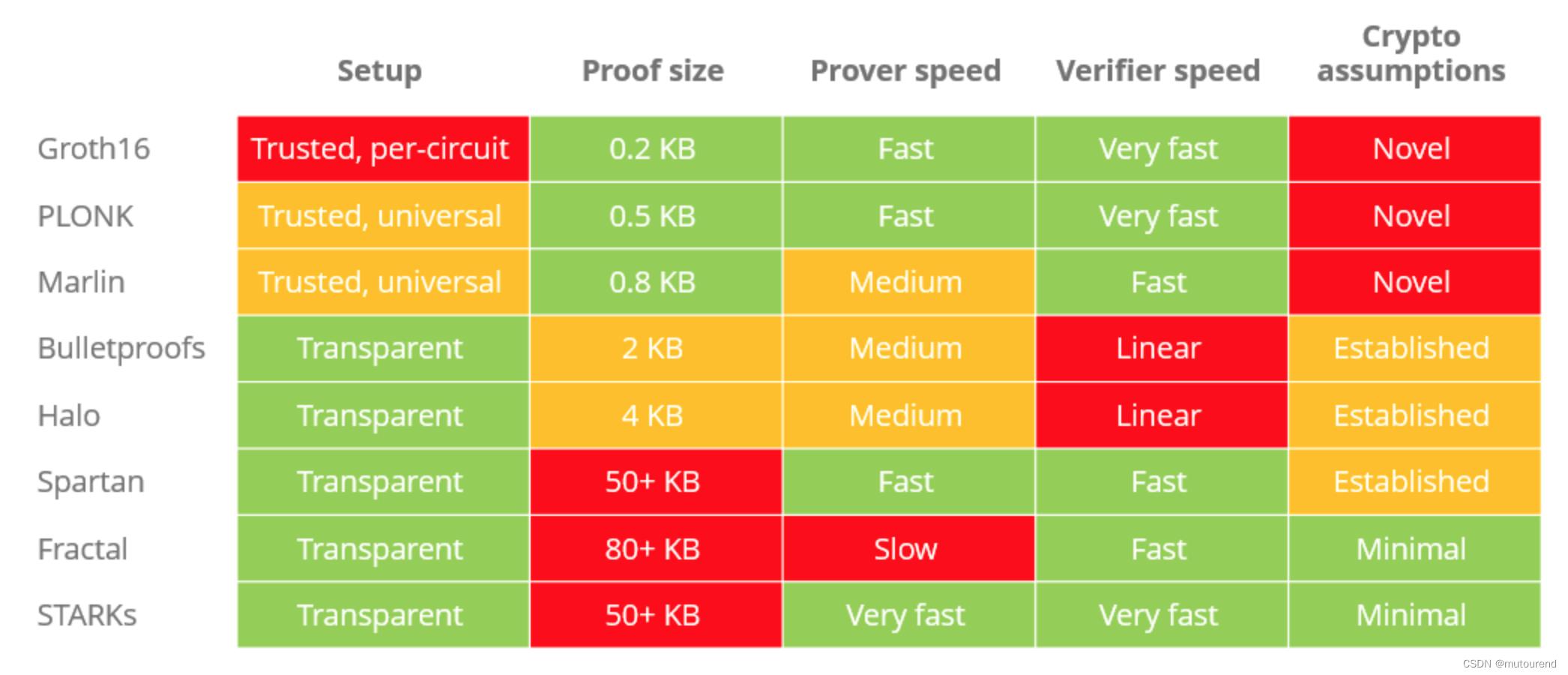
3. SNARKs VS STARKs

STARKs全称为：Scalable Transparent Arguments of Knowledge
SNARKs全称为：Succinct Non-interactive Arguments of Knowledge

STARKs与SNARKs的交叉区域有：

• Non-interactive STARKs
• Scalable Transparent SNARKs

3.1 SNARKs算术化表示 VS STARKs算术化表示

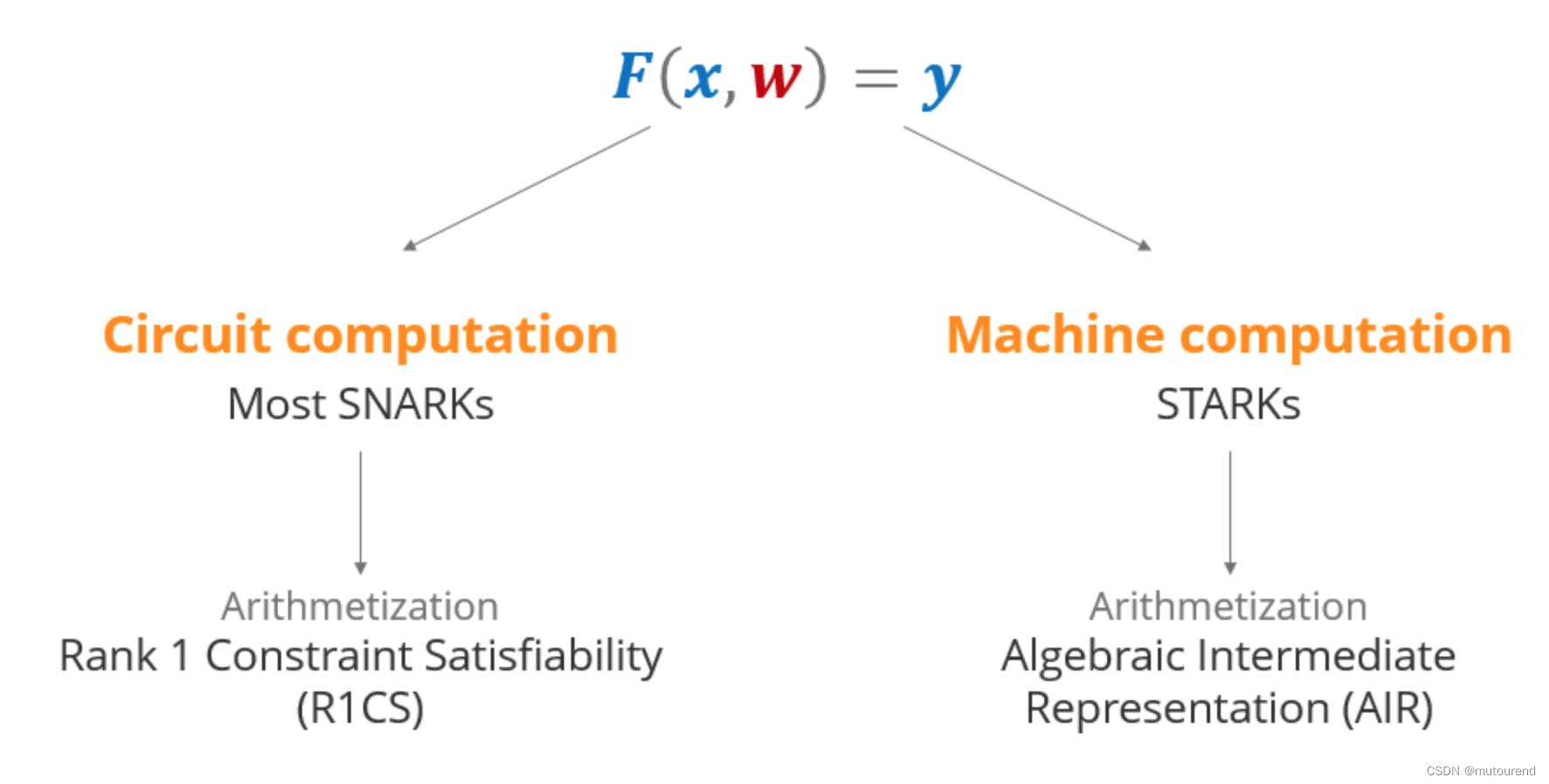
• 1）大多数SNARKs将程序表达为电路计算，以R1CS（Rank 1 Constraint Satisfiability）来表示，即：
  

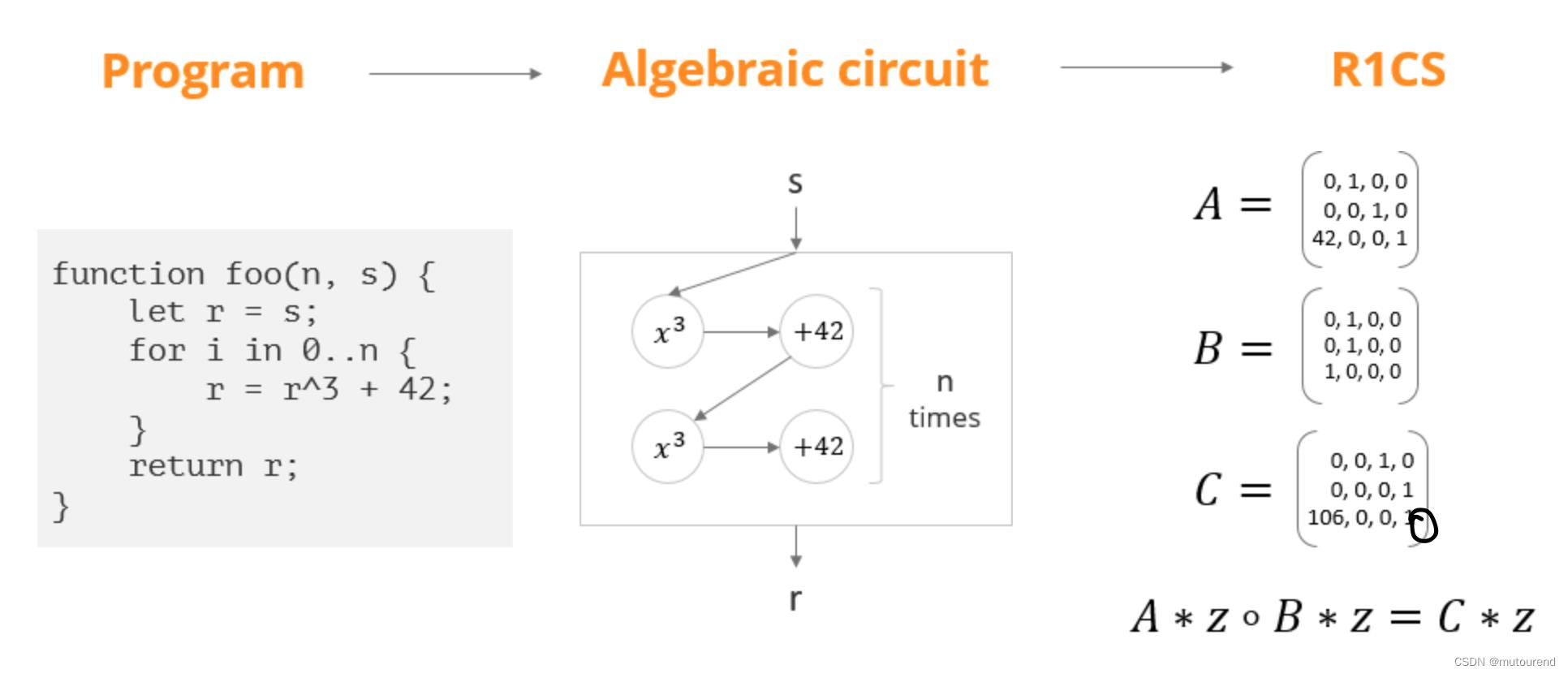
• 2）STARKs将程序表达为machine computation，以AIR（Algebraic Intermediate Representation）来表示。
  

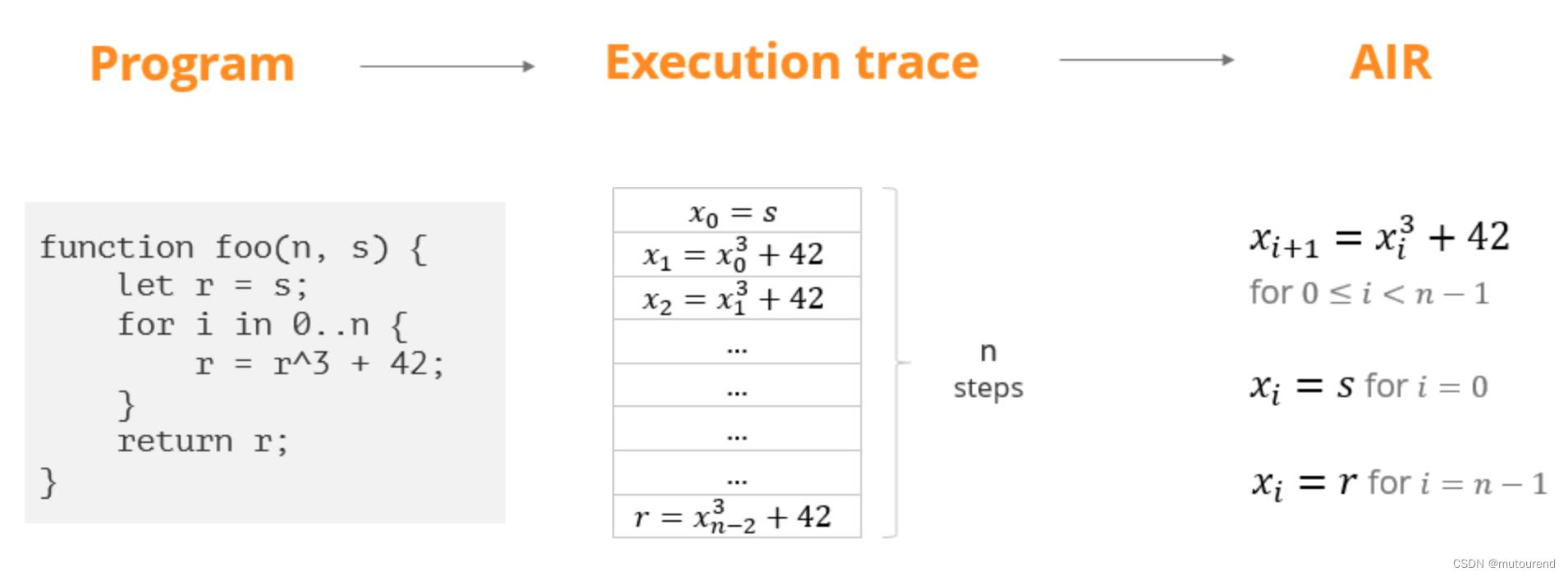
SNARKs的R1CS算术化表示 与 STARKs的AIR算术化表示 对比情况为：

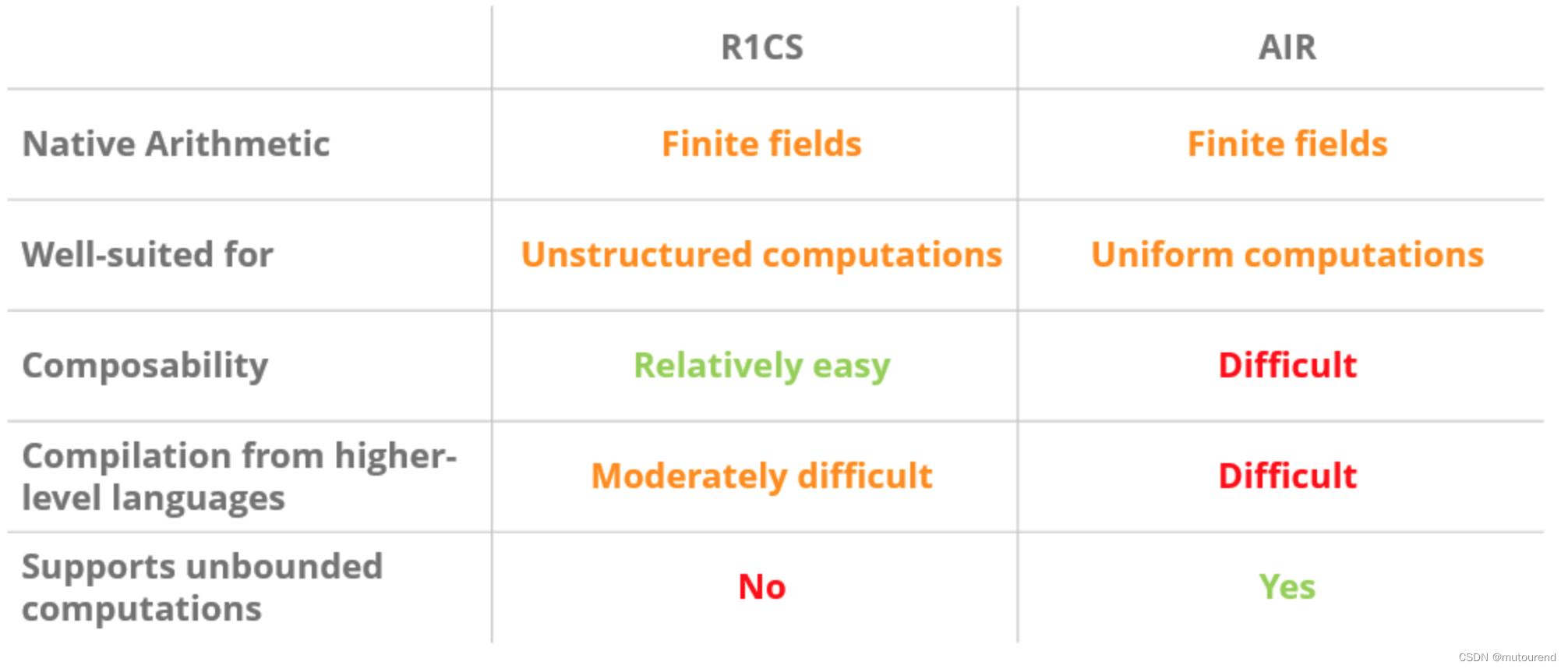
算术化友好的计算有：

• Native CPU arithmetic：如$c=a\ast b\mathrm{mod}{2}^{64}$
• Native ZKP arithmetic：如$c=a\ast b\mathrm{mod}p$，其中$p$为某素数

除此之外，ZKP系统中还包含一些昂贵的运算：

• Non-native arithmetic：如需要对输入、输出的范围进行校验。
• 比较运算，如大于、小于：需要二进制分解。
• 位运算：如AND、OR、XOR、位移等。

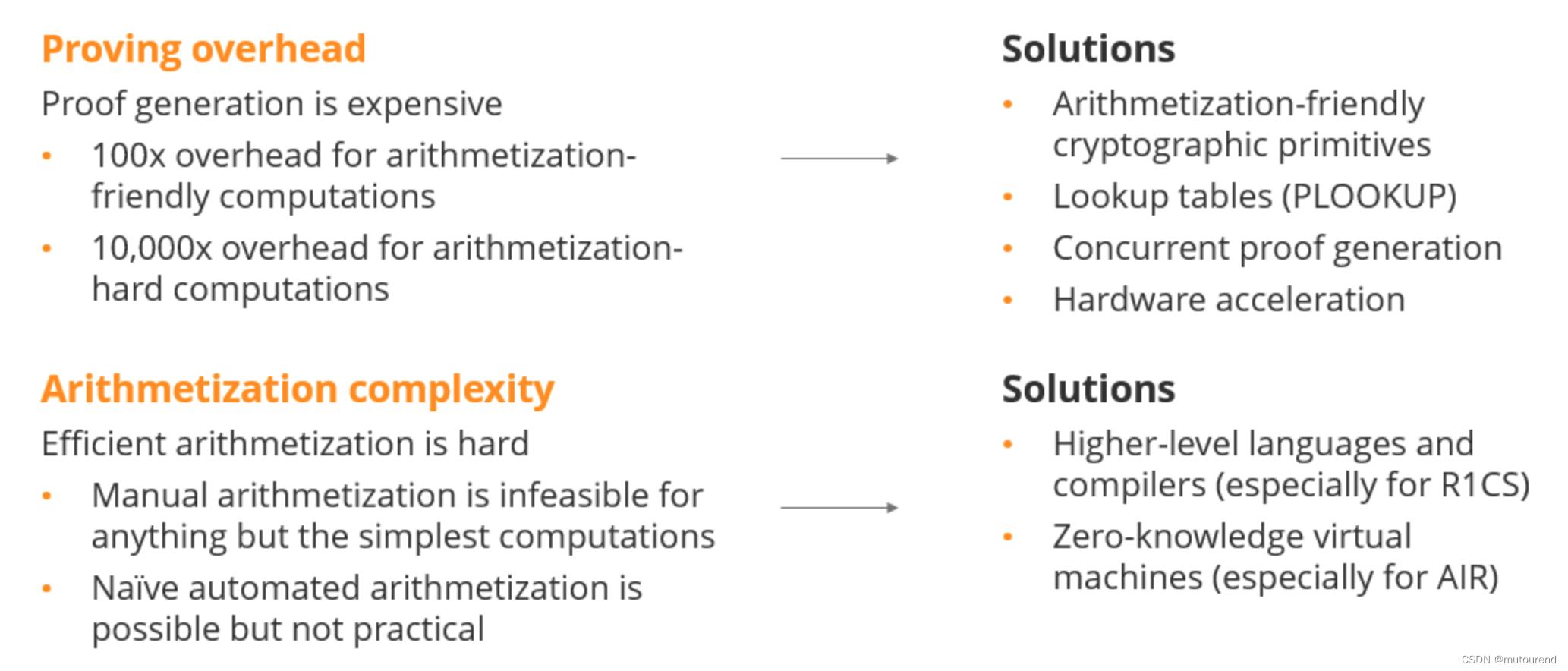
ZKP系统的主要挑战在于：

• 1）证明开销：证明生成过程是昂贵的：
  • 对于算术化友好的计算，相比于直接计算，为其生成证明需增加100倍的开销；
  • 对于算术化困难的计算，相比于直接计算，为其生成证明需增加1万倍的开销。
• 2）算术化表示复杂度：高效的算术化表示是困难的：
  • 除非是最简单的计算，否则手工算术化是不可行的；
  • 直观自动化的算术化实现是可能的，但不实用。

针对以上ZKP挑战的解决方案有：

• 1）针对证明生成昂贵问题的解决方案有：
  • 使用算术化友好的密码学原语
  • 引入lookup tables（PLOOKUP）
  • 证明生成并行化
  • 硬件加速
• 2）针对算术化表示复杂度高的问题，解决方案有：
  • 采用高层级编程语言和编译器（特别适于R1CS算术化表达）
  • 引入零知识虚拟机（特别适于AIR算术化表达）

4. ZKP用例——将ZKP用于证明计算完整性

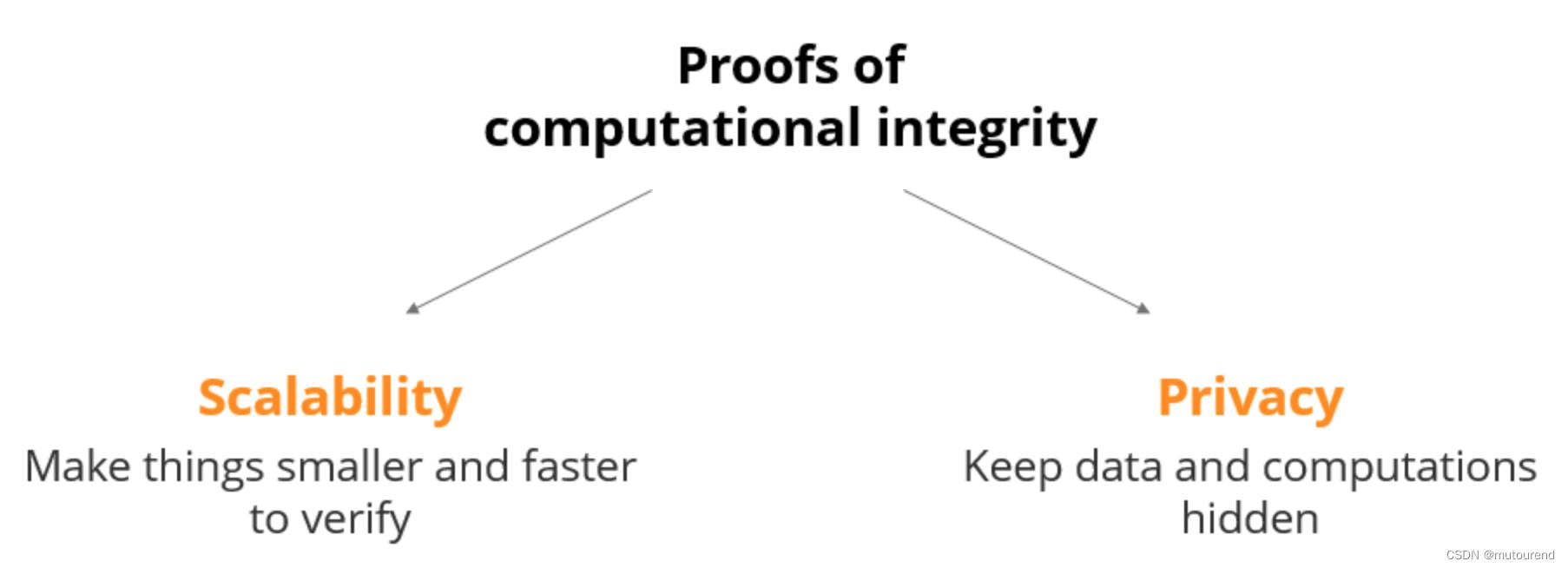
证明计算完整性需满足2个要求：

• 1）扩展性：使得验证的内容小而快，主要体现在：
  • 1.1）压缩：辅助数据可作为witness，无需与Verifier共享。
    
  • 1.2）无需重新执行：对于succinct proving system，一旦证明生成，可相比于重新执行该计算，验证该证明的速度为exponentially faster。
    
• 2）隐私性：可隐藏具体的数据和计算，具体为：
  • 2.1）数据隐私：以witness来表示隐私数据，无需对外公开。
    
  • 2.2）函数（程序）隐私：witness可对某程序编码，使得该程序也为隐私的。
    

5. 深入浅出STARKs

5.1 STARKs优缺点

STARKs的优势主要有：

• 1）Transparent：无需可信设置，无需预处理；
• 2）精干的密码学：仅需要抗碰撞哈希函数，是量子安全的；
• 3）灵活性：
  • 适于多个不同的域
  • 在Prover-time 和 proof size之间权衡
  • 在security level 和 proof size之间权衡
• 4）性能：
  • 4.1）具有超轻Verifier：
    • 大多数证明验证时间为2~5ms；
    • 具有简洁的计算描述
  • 4.2）非常快的Prover：
    • 在单核CPU上，为15K zk VM cycles/sec（对于Matic Miden VM）；
    • 可大规模并行化：在64核CPU上，速度高达400K cycles/sec。

STARKs的劣势主要有：

• 1）proof size：为数十KB：
  • 约15KB for preimage of Rescue哈希函数
  • 约120KB for 1M cycles of virtual machine execution
• 2）递归有限：可实现递归STARKs，但当前未论证
• 3）算术化表示：
  • AIR算术化表示方法比R1CS更复杂；
  • 相关工具仍在开发中。

5.2 STARK证明生成

STARK证明生成流程为：

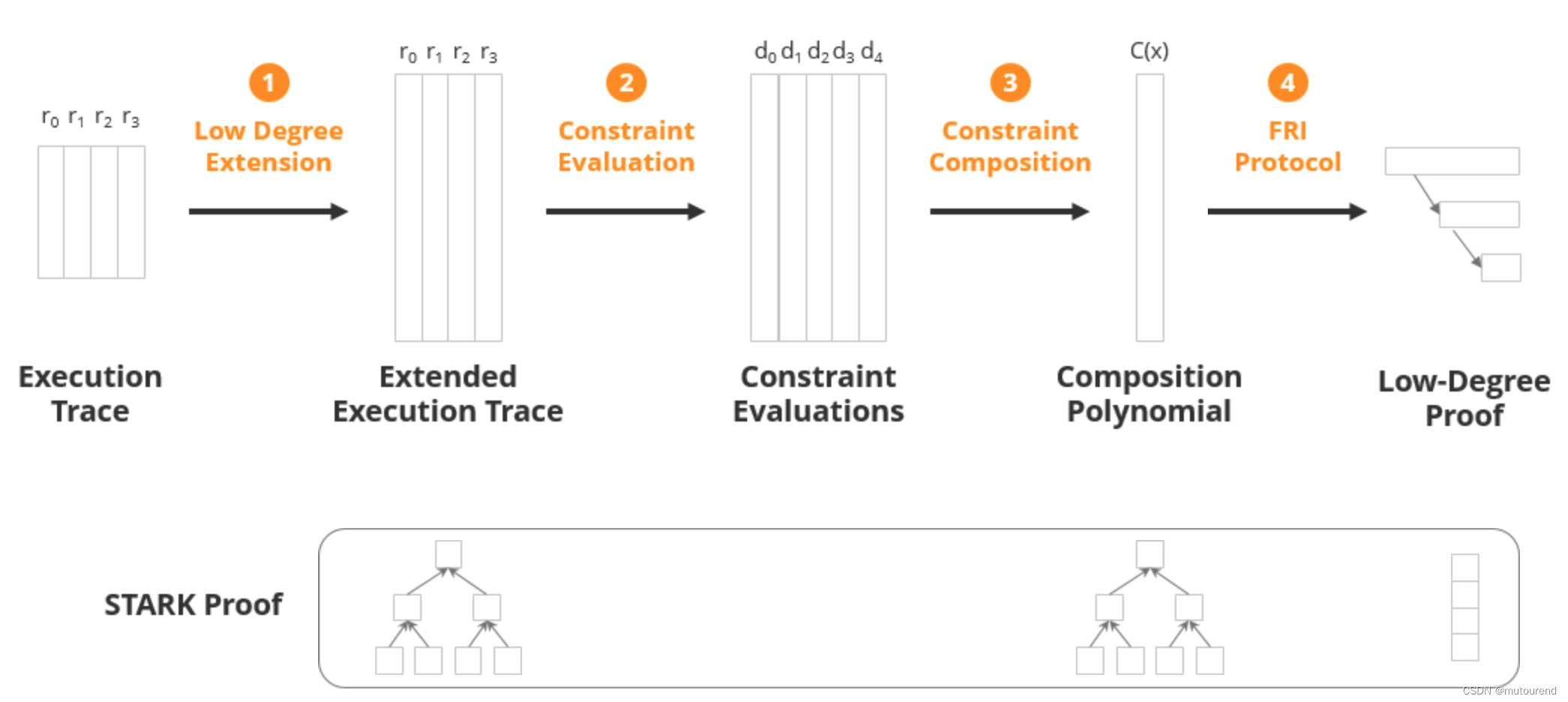
• 1）将待证明的计算 以 execution trace表示；
• 2）将execution trace的每列（寄存器）的值作为某多项式的$f(x)$的evaluations，基于trace domain $D_{trace}$插值获得$f(x)$，然后再基于更大的evaluation domain $D_{lde}$对$f(x)$进行evaluate。
• 3）定义transition constraints和boundary constraints等约束，以多项式$p(x)$来表示。
• 4）对多项式$p(x)$采用FRI协议进行证明。

5.2.1 STARK Execution trace

STARK第一步Execution trace的核心思想为：

• 1）为待证明的计算 定义state transition logic，即transition function；
• 2）运行该transition function $n$步；
• 3）记录在每步计算中，transition function的结果。

比如，在32-bit素数域内（如模为：$125\ast 2^{25}+1$，与$2^{32}-3\ast 2^{25}+1$等价），计算斐波那契数列的第64项值：

• Prover待证明内容为：
  

对应的Fibonacci execution trace表达方式有：

• 1）表达方式1：$r_{i+2}=r_{i+1}+r_i$
  相应的execution trace参数为：
  • 寄存器：1个
  • 计算步数：64步
  • 域模：$125\ast 2^{25}+1$
    
• 2）表达方式2：$r_{0,i+1}=r_{0,i}+r_{1,i}$ 以及 $r_{1,i+1}=r_{0,i}+2\ast r_{1,i}$
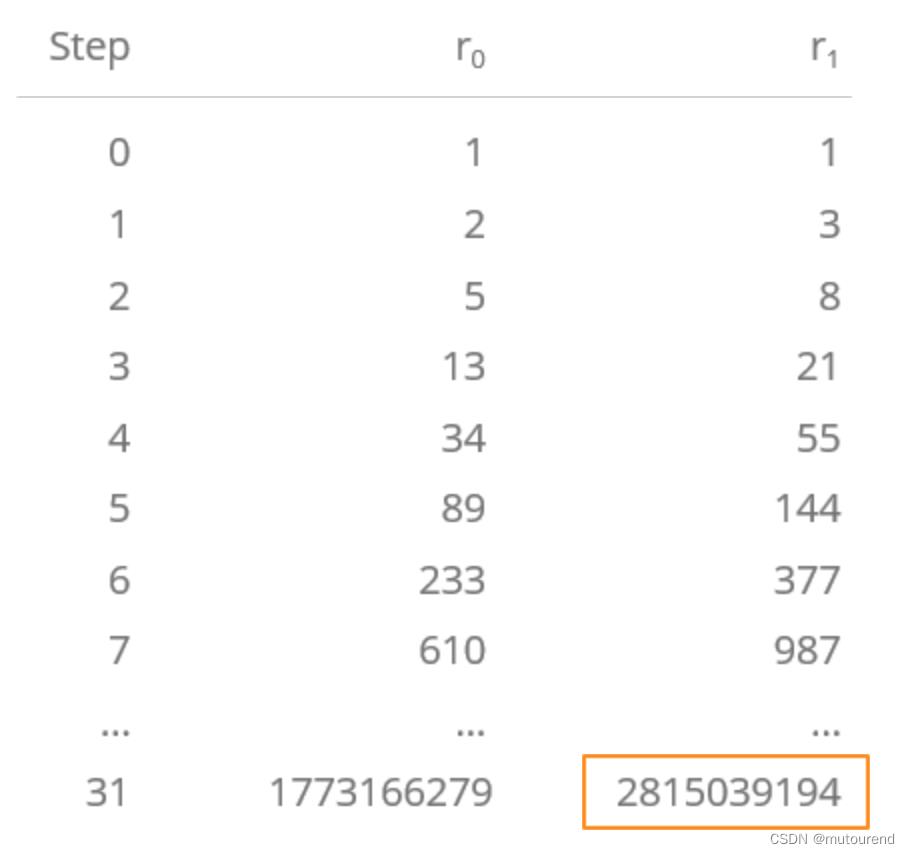
  相应的execution trace参数为：
  • 寄存器：2个
  • 计算步数：32步
  • 域模：$125\ast 2^{25}+1$
    

5.2.2 STARK Low Degree Extension

STARK Low Degree Extension（LDE）核心思想为：

• 1）将每个register trace解析为某多项式$f(x)$的evaluations；
• 2）基于某trace domain $D_{trace}$，对$f(x)$进行插值。
  如以execution trace的某register列（$r_0=y_0,y_1,y_2,y_3$）为例，基于trace domain $D_{trace}=x_0,x_1,x_2,x_3$ 插值获得的$f(x)$多项式为：【多项式$f(x)$的degree为$|D_{trace}|-1$】
  
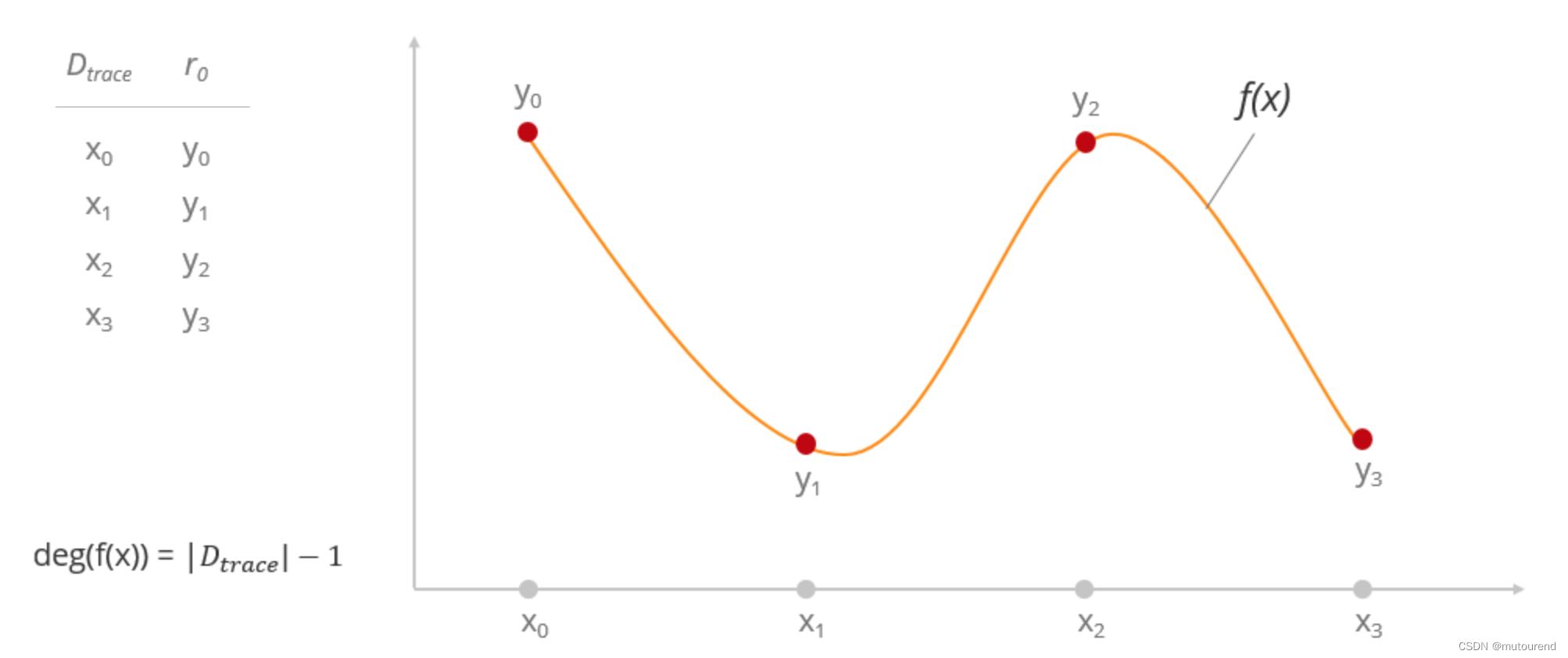
• 3）基于某更大的evaluation domain $D_{lde}$，对$f(x)$进行evaluate。
  基于更大的evaluation domain $D_{lde}=x_0^{\prime },x_1^{\prime },x_2^{\prime },x_3^{\prime },x_4^{\prime },x_5^{\prime },x_6^{\prime },x_7^{\prime }$