Polygon zkEVM中的Recursive STARKs

Posted 2023-03-05 mutourend

1. 引言

主要参看Polygon zkEVM创始人Jordi在2023年StarkWare Sessions上的分享：

• StarkWare Sessions 23 | Recursive STARKs in the zkEVM Context | Jordi Baylina

整个Polygon zkEVM circuit为一个巨大的STARK circuit。
Polygon zkEVM目前采用的递归聚合方案为：

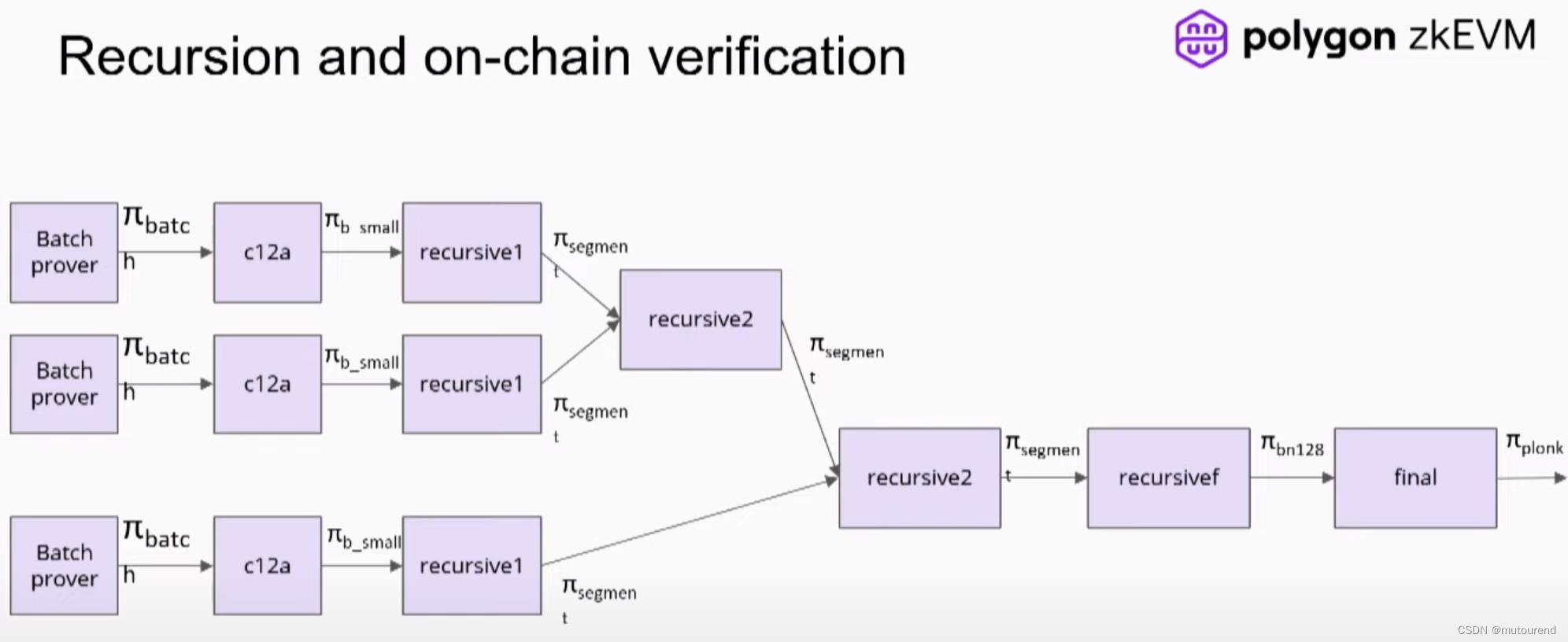
其中：

• 1）zkEVM batch prover（对应原始的zkEVM circuit）的公开输入有：
  

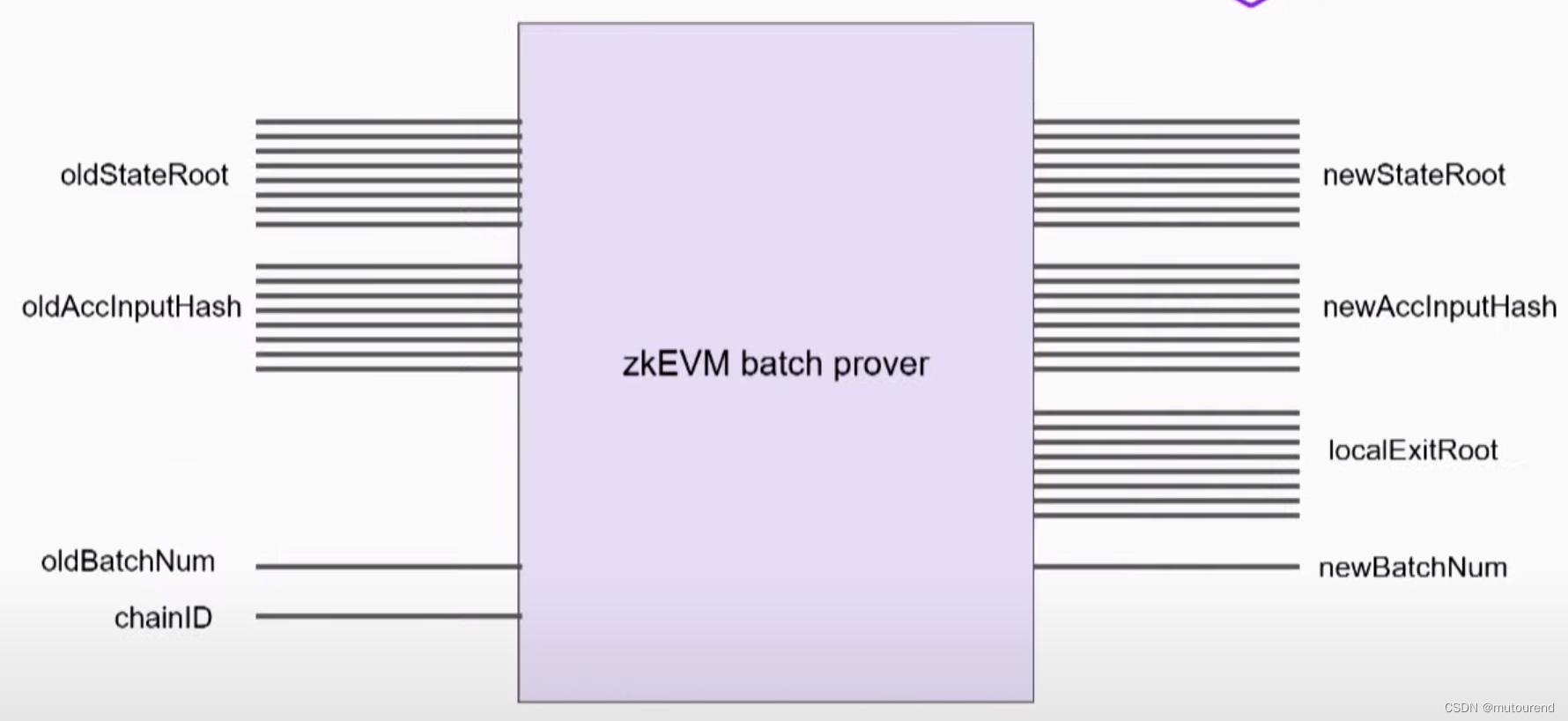
  • 1.1）其中的oldAccInputHash和newAccInputHash的计算规则为：【zkEVM batch prover（对应原始的zkEVM circuit）的隐私输入有：TXs、globalExitRoot、timestamp、sequencerAddr。】
    将Sequencer所打包交易 借助Keccak哈希进行累加：【实际是对所有L2区块进行累加】
    
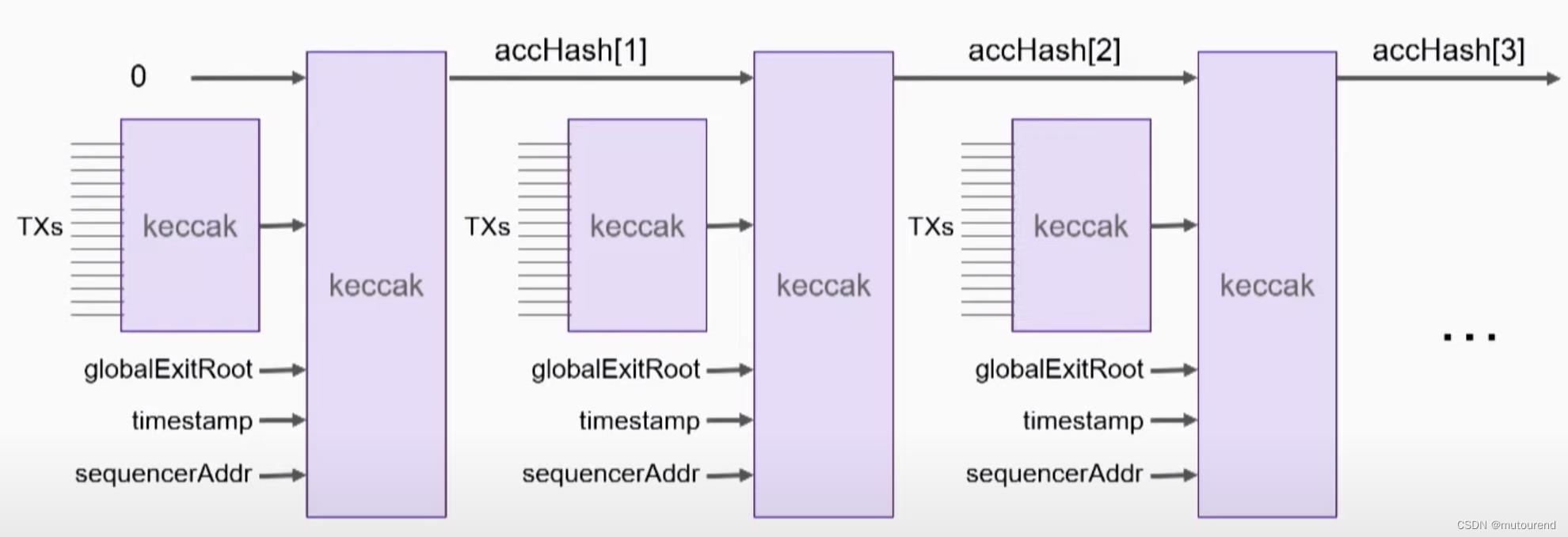
  • 1.2）localExitRoot：主要用于bridge合约中，transfer information from L2 to L1。
  • 1.3）zkEVM batch prover输出的为a huge STARK zkEVM proof ${\pi }_{batc}$。具体Polygon zkEVM的统计数据为：
    • committed多项式数量：669个
    • permutation checks数量：18个
    • plookups数量：29个
    • connection checks数量（copy constraints数量）：2个
    • columns总数：1184个
    • 多项式degree（行数）：$n=2^{23}$
    • constraint多项式最大degree：$3n$
    • blowup factor：2
    • 证明生成时间：129秒（2分钟+）
    • ${\pi }_{batc}$ proof size：1.9M（将近2MB）

• 2）由于zkEVM batch prover输出的 STARK proof ${\pi }_{batc}$ 很大，无法直接在链上验证。对huge STARK zkEVM proof ${\pi }_{batc}$做的第一件事是：

  • 2.1）借助C12a CIRCOM circuit，通过"做a proof of a proof"来对huge STARK zkEVM proof ${\pi }_{batc}$进行reduce【然后创建具有单个proof的第一层递归】。
    C12a CIRCOM circuit的公开输入 与 zkEVM batch prover（对应原始的zkEVM circuit）的公开输入 一样，不同之处在于其隐私输入不再是TXs，而是zkEVM batch prover输出的将近2MB的huge STARK zkEVM proof ${\pi }_{batc}$。
    

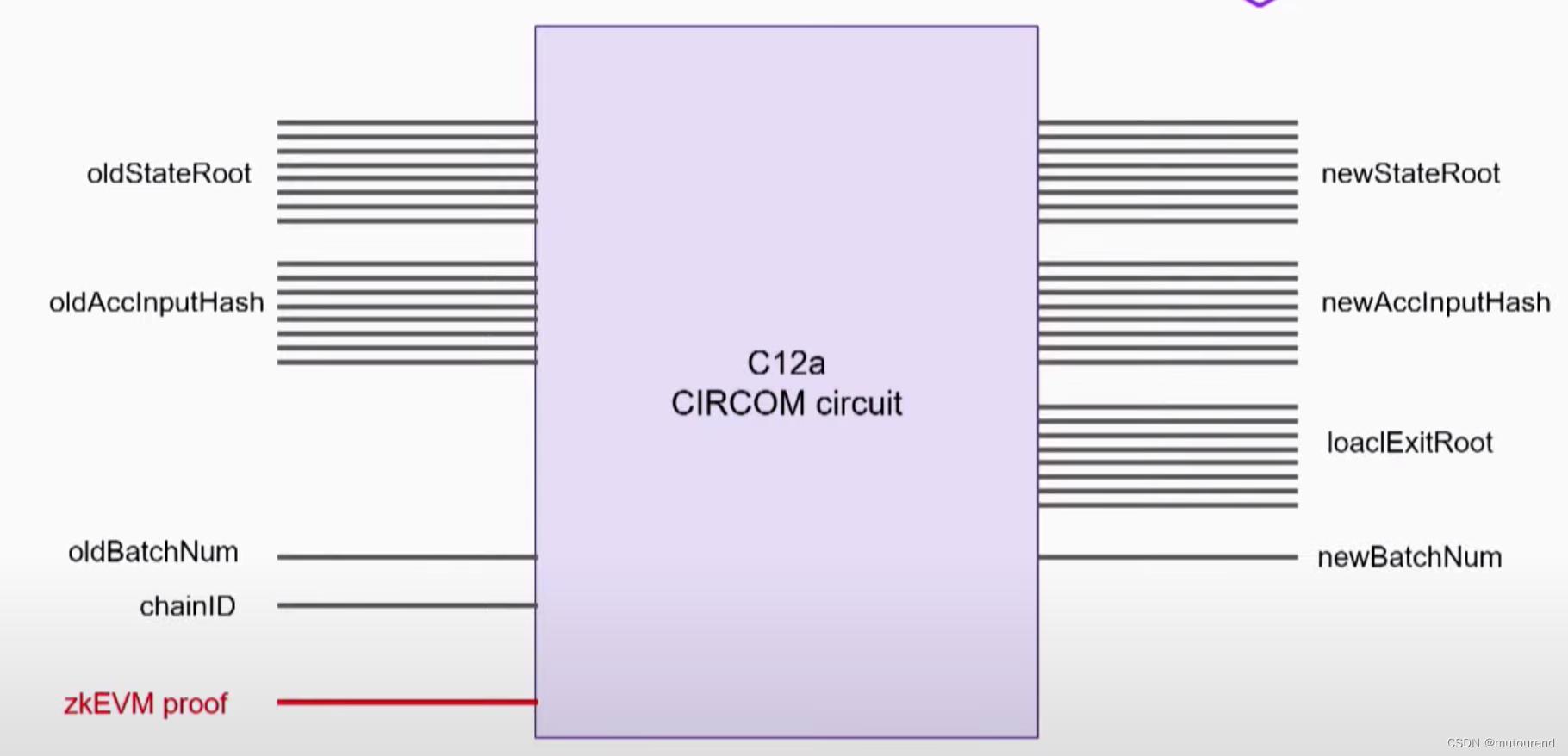
  • 2.2）C12a CIRCOM circuit以CIRCOM语言编写，事实上Polygon zkEVM团队实现了相关工具，可：【详细可参看Polygon zkEVM的pil-stark Fibonacci状态机初体验。】

    • 将“任意以PIL语言 编写的电路（如zkevm.pil）” 自动转换为“以CIRCOM语言编写的 Verifier验证该电路proof所需的电路（如zkevm.verifier.circom）”
    • 借助CIRCOM工具将*.circom转换为*.r1cs（如zkevm.verifier.r1cs）
    • 然后再将*.r1cs转换为“PIL语言编写的Verifier电路*.pil（如c12a.pil）”

  • 2.3）C12a CIRCOM circuit，由CIRCOM到PIL的整个过程中：

    • Circom采用的均为Goldilocks域
    • 有12列Signals
    • Gates：
      • 标准的PLONK gates（每行有4个PLONK gate）
      • Poseidon STEP（12个inputs，12个outputs）。一个Poseidon STEP占用2行。整个Poseidon哈希需要31行。
      • FFT4：为FFT of 4 elements in extension 3（12个inputs，12个outputs）。一次FFT4运算占用2行。FFT4为构建更大FFT运算的基石。
      • D=A*B+C in extension 3（1行）
      • Polynomial evaluation custom gate in extension3：newA=(((oldA * x + C3) * x + C2) * x + C1) *x + C0。这需要2行，可用于计算evaluations of pols of bigger size。
    • 已知某circom circuit，可将其转换为：
      • a PIL（如c12a.pil）
      • a constants polynomial（如c12a.const）
      • a witness computation program（如c12a.exec）

  • 2.4）C12a CIRCOM circuit统计数据为：

    • committed多项式数量：12个
    • permutation checks数量：10个
    • plookups数量：0个
    • connection checks数量（copy constraints数量）：1个
    • columns总数：65个
    • 多项式degree（行数）：$n=2^{22}$
    • constraint多项式最大degree：$5n$
    • blowup factor：4
    • 证明生成时间：14秒（证明时长由2分多钟，变为，14秒）
    • ${\pi }_{b\_small}$ proof size：494K（将STARK proof ${\pi }_{batc}$由约2MB，变为，约0.5MB）

• 3）recursive1 CIRCOM circuit：与c12a CIRCOM circuit类似，只是额外增加了一个公开输入：rootC。recursive1 CIRCOM circuit的隐私输入为c12a proof ${\pi }_{b\_small}$。
  
  recursive1 circuit生成的证明表示为${\pi }_{segmen}$。
  recursive1 CIRCOM circuit会生成一个recursive1Verifier CIRCOM template（如recursive1.verifier.circom）：
  

• 4）recursive2 circuit：将2个recursive1Verifier CIRCOM template放在一起，用于将2个proof聚合为1个proof。
  
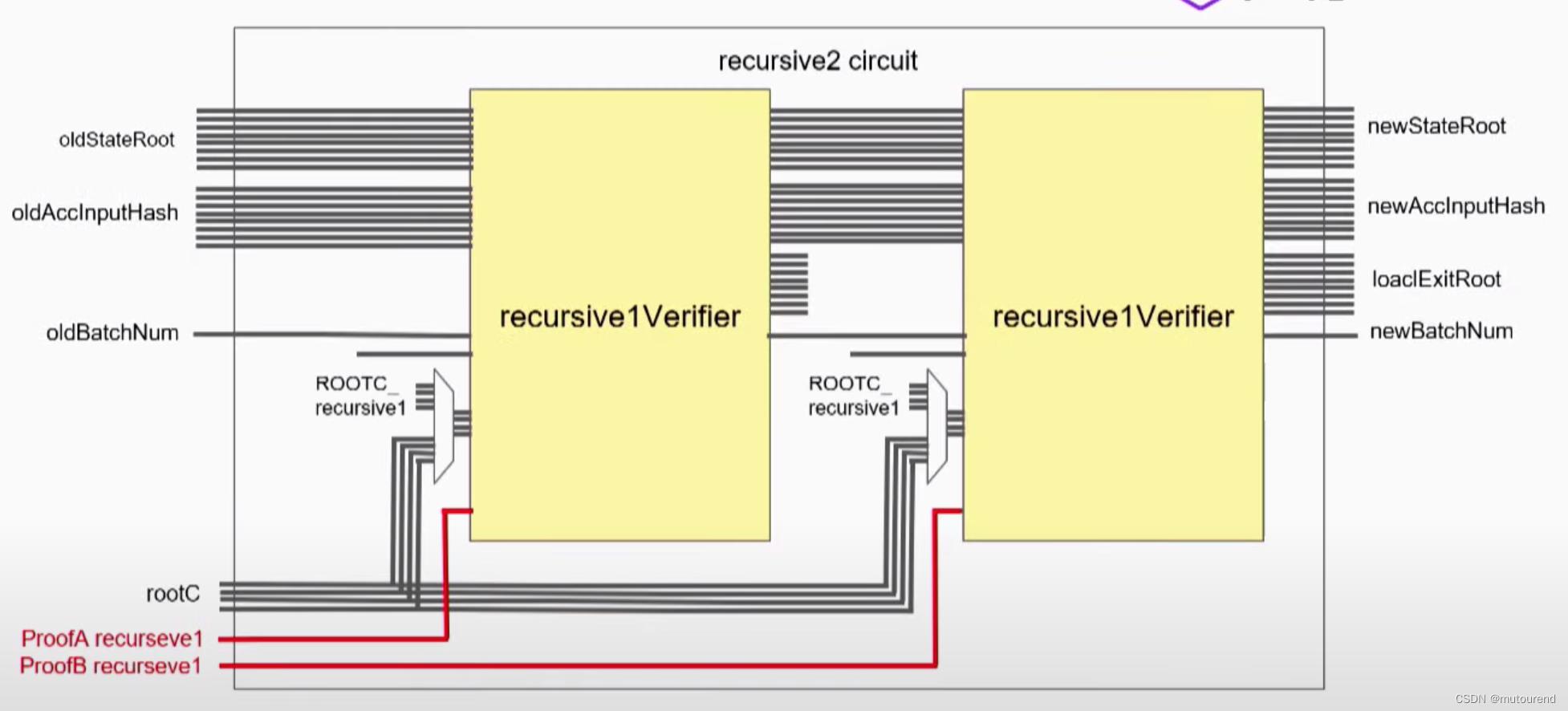
  recursive2 circuit会生成一个recursive2Verifier CIRCOM template（如recursive2.verifier.circom）：【recursive2Verifier CIRCOM template用于验证2个recursive1Verifier CIRCOM template】
  

  ---

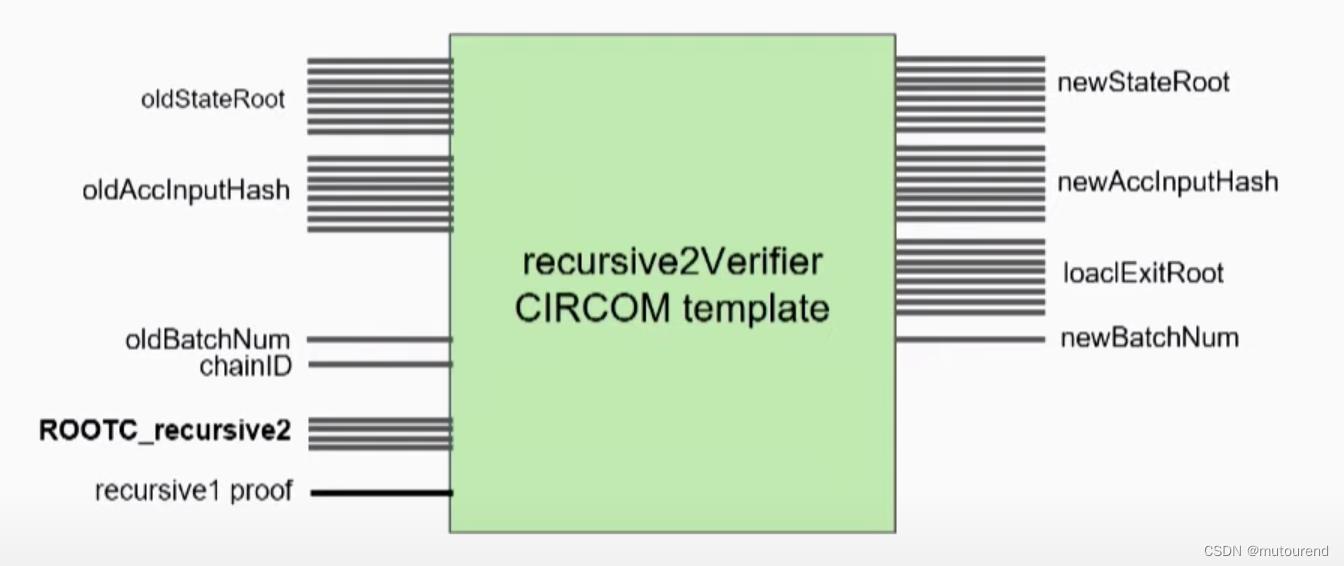
  recursive1Verifier CIRCOM template 与 recursive2Verifier CIRCOM template 二者是完全等价的：【二者唯一不同之处在于constant root，而此时将constant root rootC作为公开输入，因此二者是完全等价的。这两个模板的代码也是完全一样的。】
  
  从而可将recursive2 circuit表示为：【此时不再仅限于是对2个recursive1 proof的聚合，还支持recursive1 proof与recursive2 proof的聚合，以及聚合后的proof与“recursive1 proof或recursive2 proof”的聚合，以此类推，从而实现了递归聚合。仅需要在公开输入rootC中来区分究竟是哪种proof。从而不受限于顺序执行聚合证明，而可以并行执行，自由地选择聚合组合。】
  
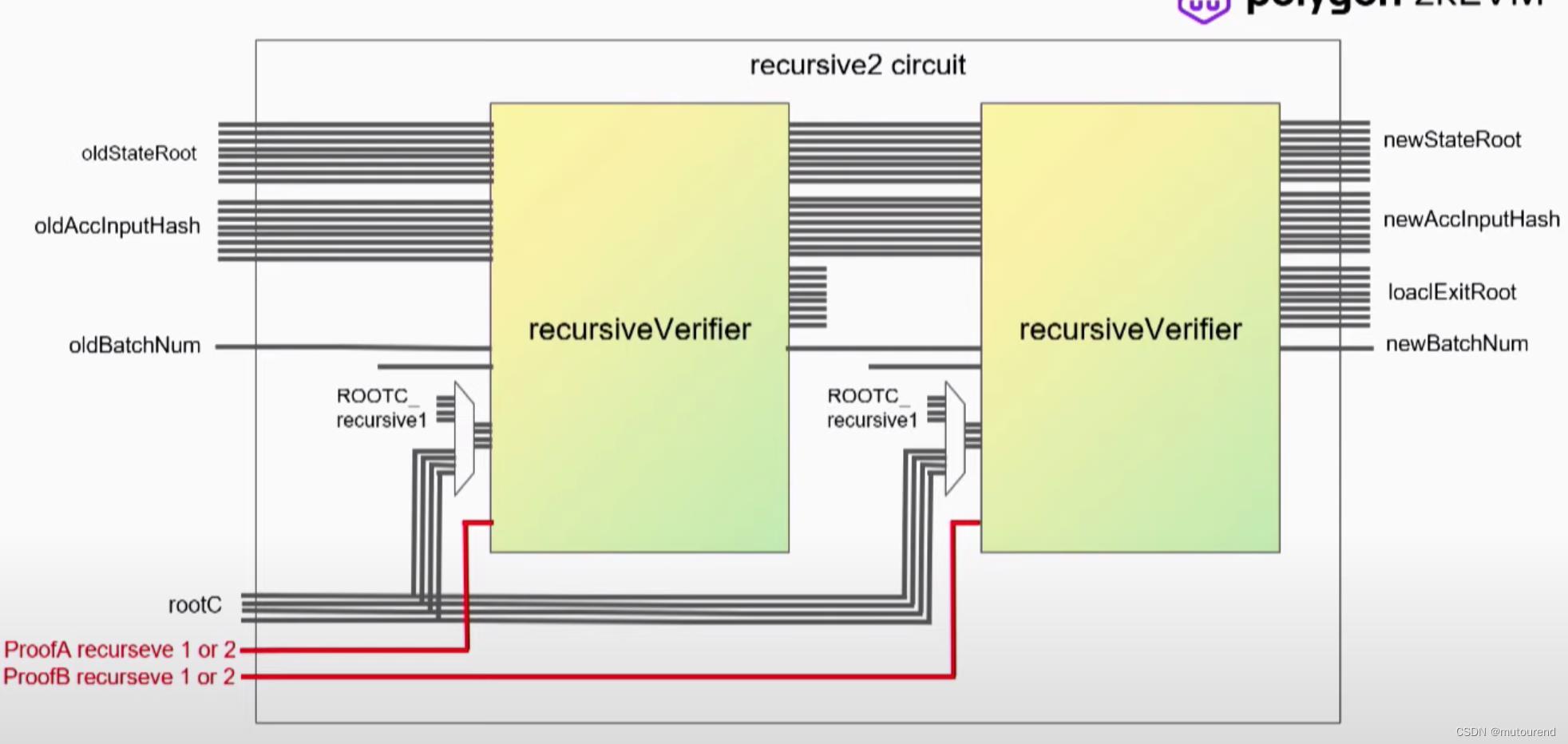
  因此，recursive2 circuit生成的证明也表示为${\pi }_{segmen}$。
  recursive1 circuit与recursive2 circuit二者等价，其统计数据为：

  • committed多项式数量：12个
  • permutation checks数量：0个
  • plookups数量：0个
  • connection checks数量（copy constraints数量）：1个
  • columns总数：45个
  • 多项式degree（行数）：$n=2^{20}$
  • constraint多项式最大degree：$9n$
  • blowup factor：16
  • 证明生成时间：10秒
  • ${\pi }_{segmen}$ proof size：约260K

  ---

• 5）recursivef circuit：为将proof提交上链做准备的一环。其本质与之前的recursiveVerifier template类似，不同之处在于，此时已知究竟是recursive1 constant还是recursive2 constant，所以此时将ROOTC_recursive2 force到了电路中。此时的STARK中的哈希运算是基于BN128域Poseidon哈希的，而不是之前的Goldilocks域。
  
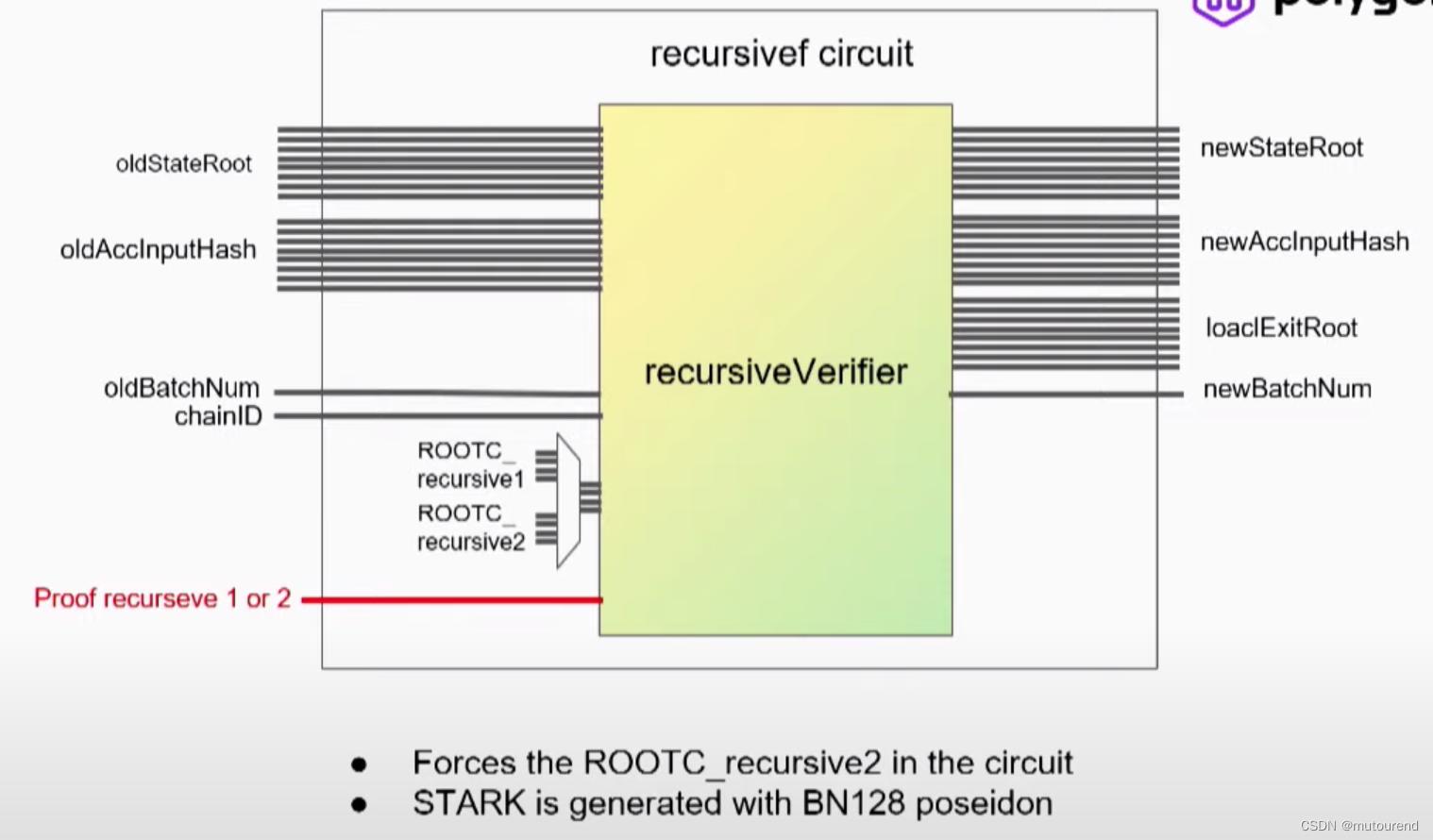
  recursivef circuit的统计数据为：

  • committed多项式数量：12个
  • permutation checks数量：0个
  • plookups数量：0个
  • connection checks数量（copy constraints数量）：1个
  • columns总数：45个
  • 多项式degree（行数）：$n=2^{19}$
  • constraint多项式最大degree：$9n$
  • blowup factor：16
  • 证明生成时间：17秒
  • ${\pi }_{bn128}$ proof size：约505K

• 6）final circuit：生成提交上链的proof，为减少上链数据，final circuit会借助SHA256将所有public input压缩为一个public input上链，将原有的public input作为隐私输入：
  
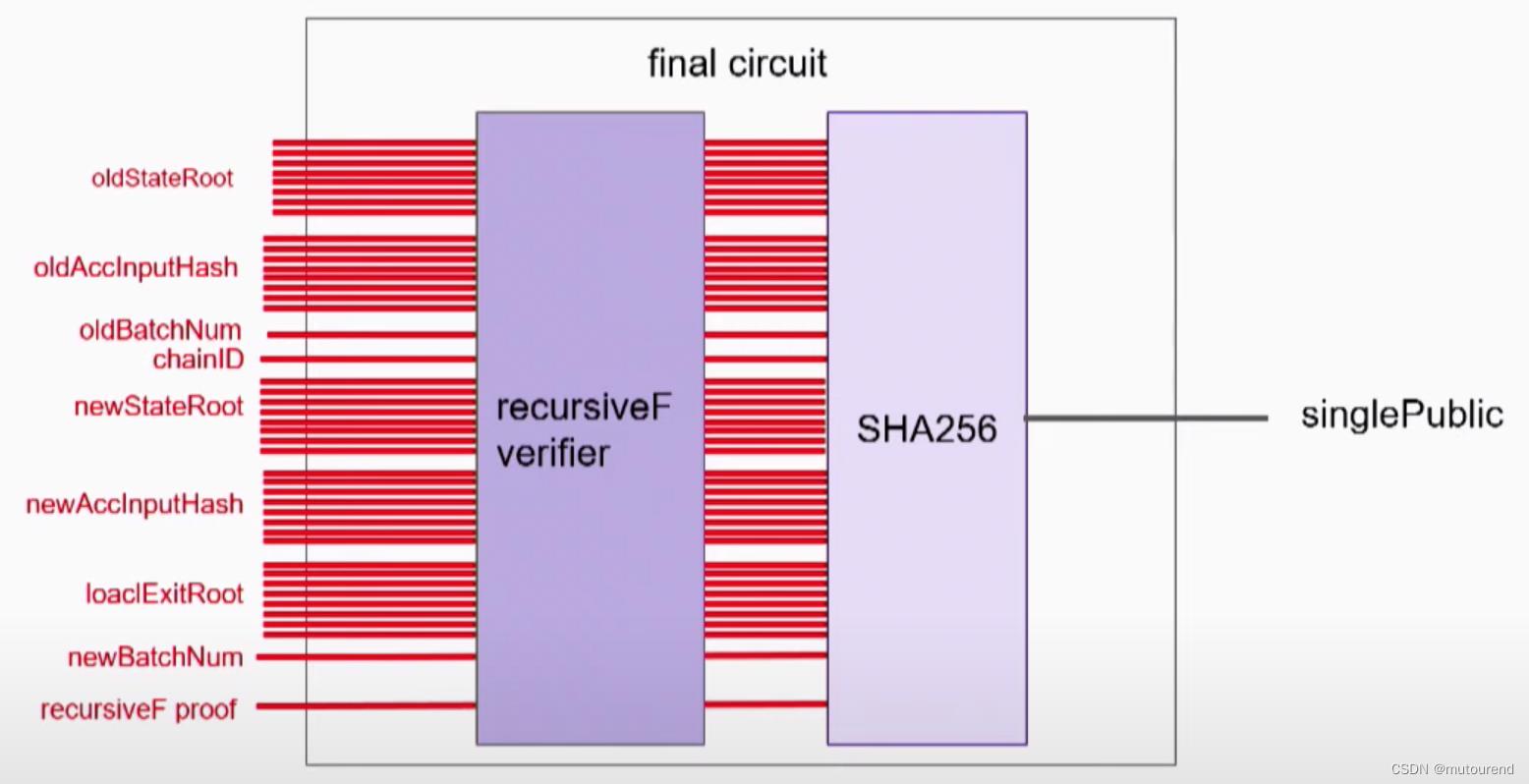
  final circuit的统计数据为：

  • 约束数：800万
  • 证明生成时间：11秒
  • ${\pi }_{plonk}$ proof size：小于1K
  • Gas开销：362K（Full proving TX）

  ---

  Polygon zkEVM计划于2023年主网上线，并将final circuit中的Groth16改为FFLONK方案，原因在于：

  • FFLONK的证明时长为Groth16的2倍
  • FLLONK证明的链上验证Gas开销要略低于Groth16的
  • FFLONK不需要specific trusted setup，仅需要universal trusted setup

  根据Polygon zkEVM创始人Jordi 2023年2月twitterFFLONK已在snarkJS中实现，开源代码见：

  • https://github.com/iden3/snarkjs/tree/master/src（javascript）

  FFLONK为类似Groth16或PLONK的zkSNARK协议，主要优势在：

  • 1）无需specific trusted setup（仅需universal setup）。
  • 2）链上验证proof的开销比Groth16要便宜一点点，比常规的PLONK便宜30%。【以Polygon zkEVM为例，采用fflonk的链上验证开销为20.3万Gas，而Groth16为23万Gas，PLONK为30万Gas。】

  Polygon zkEVM仅在proof的最后recursive阶段使用SNARK来聚合多个batch proofs，相应的电路将相对small，且链上验证开销可分摊在多个batch proofs中。Polygon zkEVM的当前最后证明时间约为2分钟，目标是优化后达到少于1分钟。当审计完成后，将在Polygon zkEVM主网中使用fflonk。

  ---

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理
• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束
• Polygon zkEVM Merkle tree的circom约束
• Polygon zkEVM FFT和多项式evaluate计算的circom约束
• Polygon zkEVM R1CS与Plonk电路转换
• Polygon zkEVM中的子约束系统
• Polygon zkEVM交易解析
• Polygon zkEVM 审计及递归证明
• Polygon zkEVM发布公开测试网2.0
• Polygon zkEVM测试集——创建合约交易