聚类算法（K-means & AGNES & DBSCAN）

Posted 2022-08-15 clarkjs

一、聚类算法基本概念

1. 定义：

聚类就是按照某个特定标准(如距离准则)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大。即聚类后同一类的数据尽可能聚集到一起，不同数据尽量分离。简单来讲就是把相似的东西分到一起。

2. 无监督学习

我们一定要区分开聚类算法和分类算法。分类算法是训练一个分类器，根据已知的事物和对应的标签进行学习、训练，属于有监督学习。而聚类算法仅仅是把相似的事物分成一组，没有标签，属于无监督学习。

3. 常见的聚类算法

主要的聚类算法可以划分为如下几类：（1）划分方法 （2）层次方法 （3）基于密度的方法 （4）基于网格的方法 （5）基于模型的方法。本讲主要介绍以下三种聚类算法👇：

二、聚类算法

1. K-means聚类算法

（1）K-means 基本概念

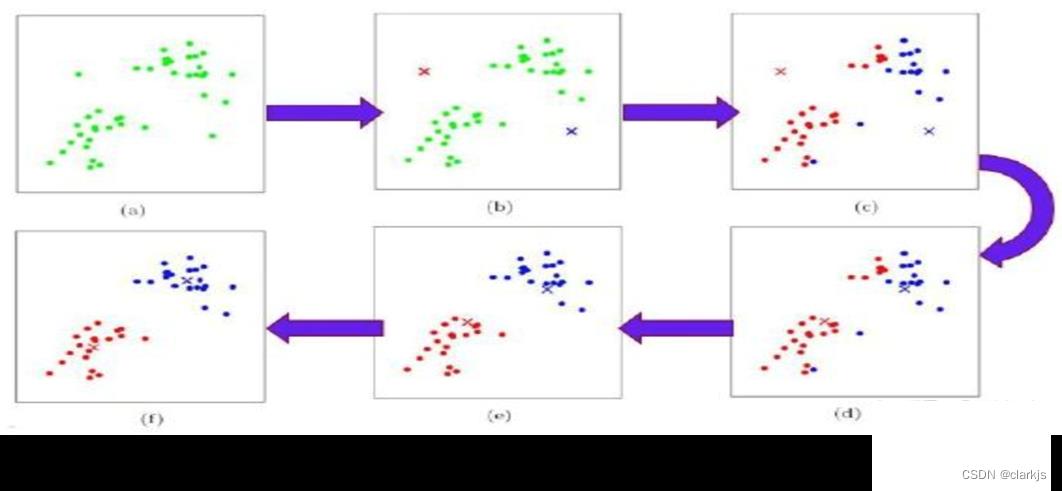
K-means（又称k-均值或k-平均）聚类算法。算法思想就是首先随机确定k个中心点作为聚类中心，然后把每个数据点分配给最邻近的中心点，分配完成后形成k个聚类，计算各个聚类的平均中心点，将其作为该聚类新的类中心点，然后重复迭代上述步骤直到分配过程不再产生变化。

（2）K-means步骤

① 从D中随机取k个元素，作为k个簇的各自的中心。
② 分别计算剩下的元素到k个簇中心的相异度，将这些元素分别划归到相异度最低的簇。
③ 根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。
④ 将D中全部元素按照新的中心重新聚类。
⑤ 重复第4步，直到聚类结果不再变化。
⑥ 将结果输出。

（3）K-means示例

① 假设K=3，首先 3 个中心点被随机初始化，所有的数据点都还没有进行聚类，默认全部都标记为红色，如下图所示：

② 然后进入第一次迭代：按照初始的中心点位置为每个数据点着上颜色，重新计算 3 个中心点，结果如下图所示：

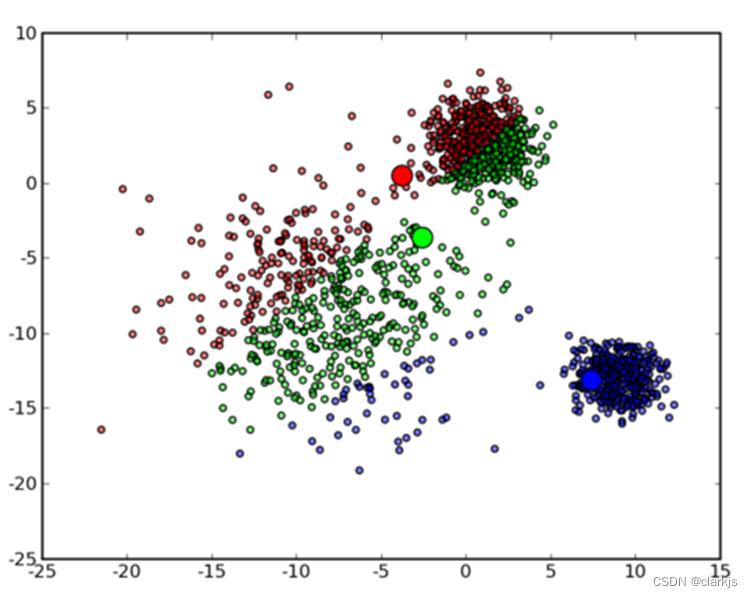
③ 根据上图可以看出，由于初始的中心点是随机选的，现在上图目测效果并不是很理想，肯定还需要继续迭代，接下来是下一次迭代的结果：

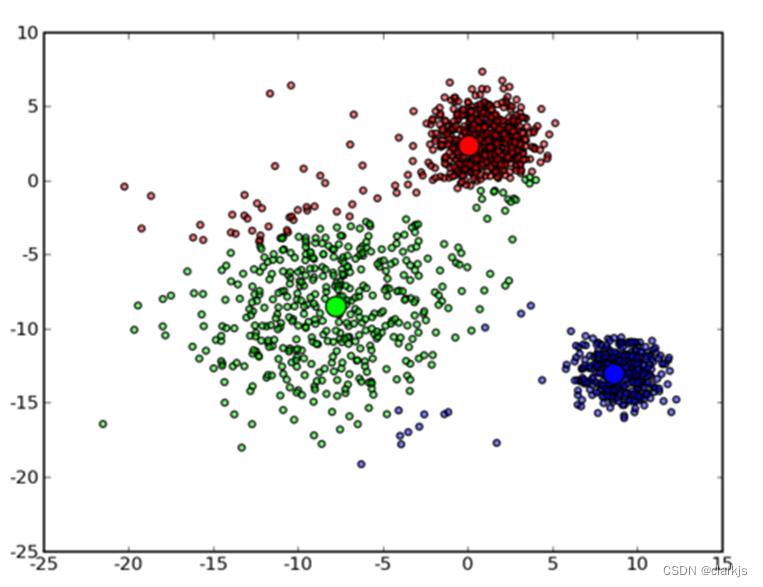
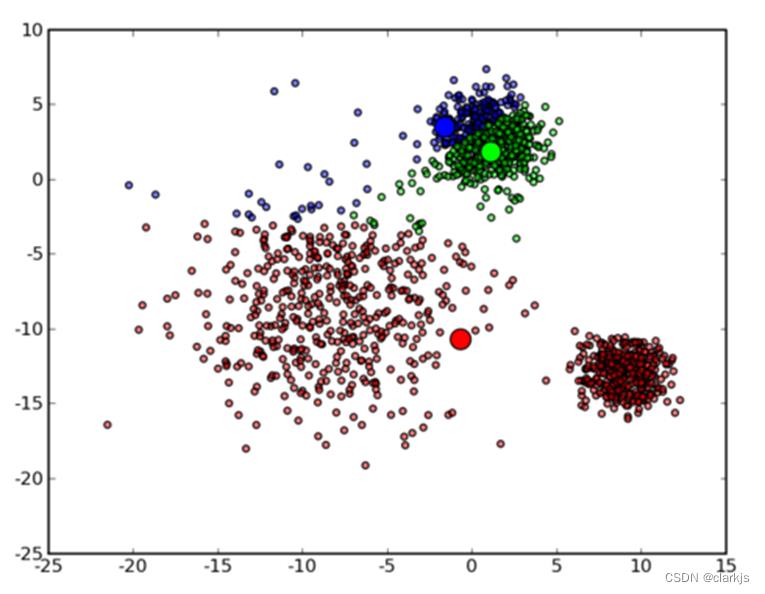
④ 可以看到大致形状已经出来了。再经过两次迭代之后，基本上就收敛了，最终结果如下：

（4）优缺点

参考1：

参考2：

注：在参考1中有一个缺点是会受初始点的选取影响，如果初始点选取很糟糕，可能导致结果很烂，举个例子，例如选用下面这几个初始中心点：

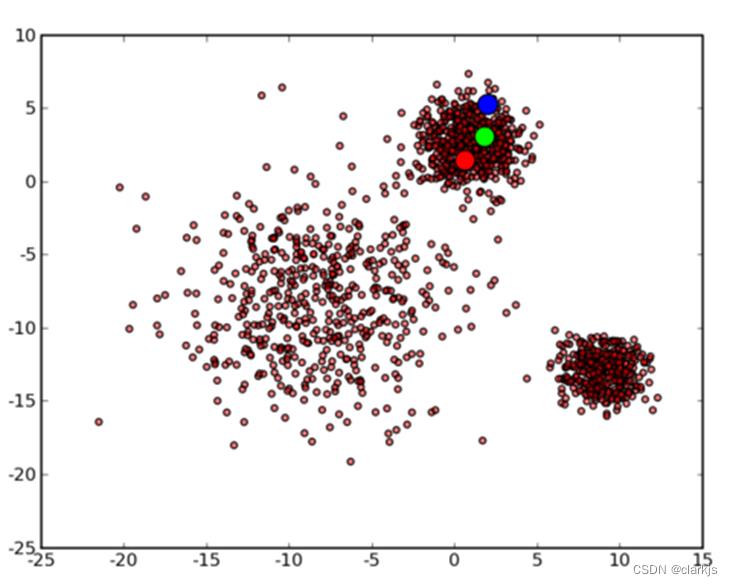
最终会收敛到这样的结果：

2. 层次聚类

（1）层次聚类基本概念

层次聚类是另一种主要的聚类方法，它具有一些十分必要的特性使得它成为广泛应用的聚类方法。它生成一系列嵌套的聚类树来完成聚类。单点聚类处在树的最底层，在树的顶层有一个根节点聚类。根节点聚类覆盖了全部的所有数据点。 可根据其聚类方式划分为：（1）凝聚（自下而上）聚类 （2）分裂（自上而下）聚类。层次凝聚的代表是AGNES算法。层次分裂的代表是DIANA算法。接下来主要介绍以下AGNES算法。

（2）AGNES算法

AGNES (AGglomerative NESting)算法最初将每个对象作为一个簇，然后这些簇根据某些准则被一步步地合并。两个簇间的相似度由这两个不同簇中距离最近的数据点对的相似度来确定。聚类的合并过程反复进行直到所有的对象最终满足簇数目。

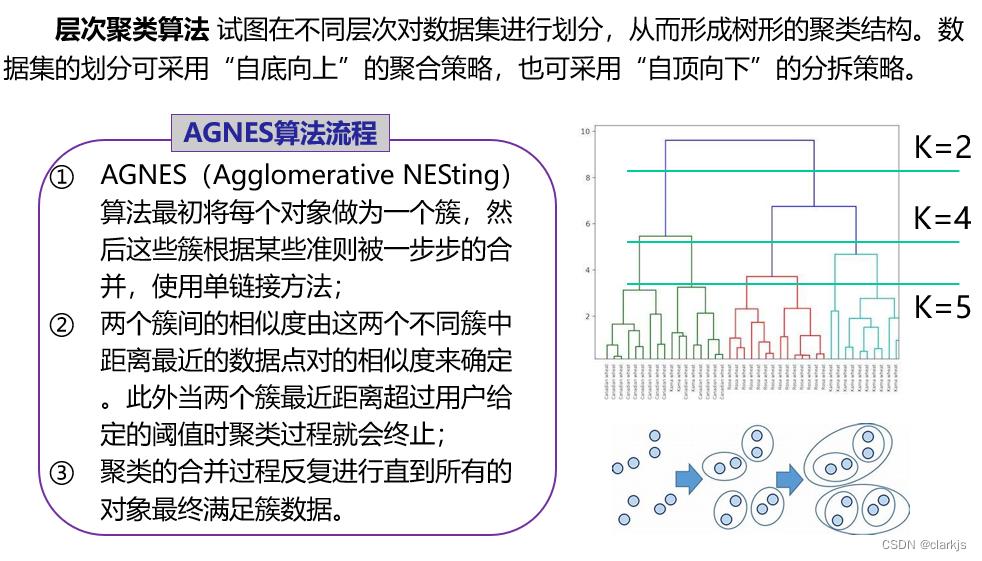
AGNES（自底向上凝聚算法）计算机编程实现： 
输入：包含n个对象的数据库，终止条件簇的数目k。 
输出：k个簇，达到终止条件规定簇数目。

将每个对象当成一个初始簇
REPEAT
    根据两个簇中最近的数据点找到最近的两个簇；
    合并两个簇，生成新的簇的集合；
UNTIL  达到定义的簇的数目

（3）判断两个簇之间相似度的方法

① SingleLinkage

SingleLinkage又叫做 nearest-neighbor ，就是取两个类中距离最近的两个样本的距离作为这两个集合的距离，也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大。
注：这个方法有一个很大的问题，当两个簇整体距离很远，但是某两个点离得很近，这会导致模型认为两个簇很想相近，导致误判。而且这样得到的簇也会很松散。

② CompleteLinkage

CompleteLinkage是 Single Linkage 的反面极端，取两个集合中距离最远的两个点的距离作为两个集合的距离。
注：这个方法的问题是，当两个簇整体距离很近，但是某两点离得很远，就永远不会合并成一个簇，导致误判。

③ Average-linkage

Average-linkage就是把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。
接下来我们利用层次聚类和Average-linkage判定相似性的方法来看一个例题吧👇：

（4）优缺点

3. 密度聚类

（1）密度聚类简介

密度聚类方法的指导思想是，只要一个区域中的点的密度大于某个域值，就把它加到与之相近的聚类中去。这类算法能克服基于距离的算法只能发现“类圆形”的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感。但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量，且对数据维数的伸缩性较差。
这类方法需要扫描整个数据库，每个数据对象都可能引起一次查询，因此当数据量大时会造成频繁的I/O操作。代表算法有：（1）DBSCAN （2）OPTICS （3）DENCLUE etc

（2）DBSCAN

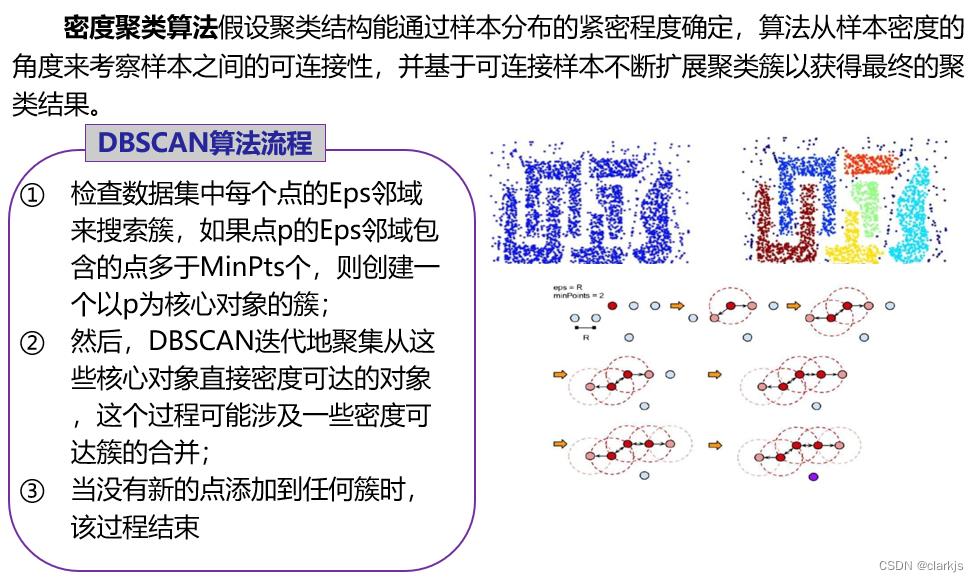
① 算法介绍

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的空间数据库中发现任意形状的聚类。了解DBSCAN，务必熟悉几个概念：
① 对象的ε-临域：给定对象在半径ε内的区域。
② 核心对象：如果一个对象的ε-临域至少包含最小数目MinPts个对象，则称该对象为核心对象。 例如，在下图中，ε=1cm，MinPts=5，q是一个核心对象：

③ 直接密度可达：给定一个对象集合D，如果p是在q的ε-邻域内，而q是一个核心对象，我们说对象p从对象q出发是直接密度可达的。上图中，对象p从对象q出发是直接密度可达的。
④ 密度可达：如果存在一个对象链p1，p2，…，pn，p1=q，pn=p，对pi∈D，（1<=i<=n），pi+1是从pi关于ε和MitPts直接密度可达的，则对象p是从对象q关于ε和MinPts密度可达的。
⑤ 密度相连：如果对象集合D中存在一个对象o，使得对象p和q是从o关于ε和MinPts密度可达的，那么对象p和q是关于ε和MinPts密度相连的。
⑥ 噪声: 一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合。不包含在任何簇中的对象被认为是“噪声”。

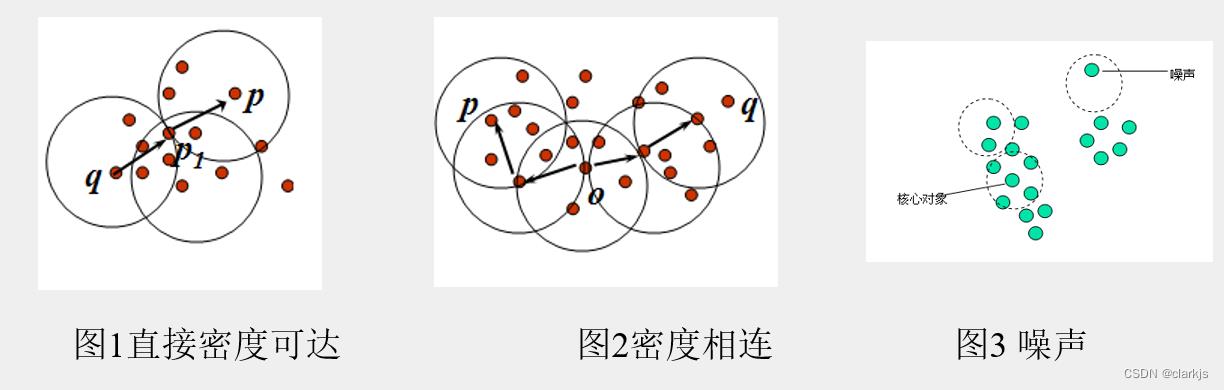
DBSCAN算法描述
输入：包含n个对象的数据库，半径ε，最少数目MinPts。
输出：所有生成的簇，达到密度要求。
1.  REPEAT
2.      从数据库中抽取一个未处理过的点；
3.      IF 抽出的点是核心点 THEN  找出所有从该点密度可达的对象，形成一个簇
4.      ELSE 抽出的点是边缘点(非核心对象)，跳出本次循环，寻找下一点；
5.  UNTIL 所有点都被处理；

② 优缺点