机器学习笔记之谱聚类k-Means聚类算法介绍
Posted 静静的喝酒
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习笔记之谱聚类k-Means聚类算法介绍相关的知识,希望对你有一定的参考价值。
机器学习笔记之谱聚类——K-Means聚类算法介绍
引言
从本节开始,将介绍聚类任务,本节将介绍 k-Means \\textk-Means k-Means算法。
回顾:高斯混合模型
高斯混合模型(
Gaussian Mixture Model,GMM
\\textGaussian Mixture Model,GMM
Gaussian Mixture Model,GMM)是一种处理聚类任务的常用模型。作为一种概率生成模型,它的概率图结构可表示为如下形式:
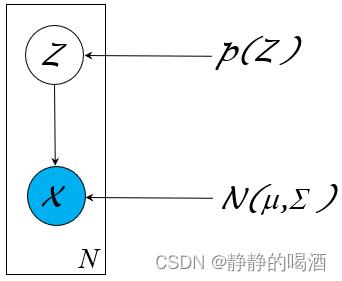
其中隐变量
Z
\\mathcal Z
Z是一个离散型随机变量,对应随机变量
X
\\mathcal X
X的后验结果服从高斯分布:
Z
∼
Categorical Distribution
(
1
,
2
,
⋯
,
K
)
X
∣
Z
∼
N
(
μ
k
,
Σ
k
)
k
∈
1
,
2
,
⋯
,
K
\\beginaligned \\mathcal Z & \\sim \\textCategorical Distribution(1,2,\\cdots,\\mathcal K) \\\\ \\mathcal X & \\mid \\mathcal Z \\sim \\mathcal N(\\mu_k,\\Sigma_k) \\quad k \\in \\1,2,\\cdots,\\mathcal K\\ \\endaligned
ZX∼Categorical Distribution(1,2,⋯,K)∣Z∼N(μk,Σk)k∈1,2,⋯,K
从生成模型的角度,高斯混合模型对
P
(
X
,
Z
)
\\mathcal P(\\mathcal X,\\mathcal Z)
P(X,Z)进行建模。关于
X
\\mathcal X
X的概率密度函数
P
(
X
)
\\mathcal P(\\mathcal X)
P(X)可表示为如下形式:
其中
P
Z
k
\\mathcal P_\\mathcal Z_k
PZk表示隐变量
Z
\\mathcal Z
Z选择离散结果
k
k
k时的概率结果;
μ
Z
k
,
Σ
Z
k
\\mu_\\mathcal Z_k,\\Sigma_\\mathcal Z_k
μZk,ΣZk表示对应
X
∣
Z
k
\\mathcal X \\mid \\mathcal Z_k
X∣Zk高斯分布的均值和协方差信息。
P
(
X
)
=
∑
Z
P
(
X
,
Z
)
=
∑
Z
P
(
Z
)
⋅
P
(
X
∣
Z
)
=
∑
k
=
1
K
P
Z
k
⋅
N
(
μ
Z
k
,
Σ
Z
k
)
\\beginaligned \\mathcal P(\\mathcal X) & = \\sum_\\mathcal Z \\mathcal P(\\mathcal X,\\mathcal Z) \\\\ & = \\sum_\\mathcal Z \\mathcal P(\\mathcal Z) \\cdot \\mathcal P(\\mathcal X \\mid \\mathcal Z) \\\\ & = \\sum_k=1^\\mathcal K\\mathcal P_\\mathcal Z_k \\cdot \\mathcal N(\\mu_\\mathcal Z_k,\\Sigma_\\mathcal Z_k) \\endaligned
P(X)=Z∑P(X,Z)=Z∑P(Z)⋅P(X∣Z)=k=1∑KPZk⋅N(μZk,ΣZk)
聚类任务基本介绍
在生成模型综述——监督学习与无监督学习中简单介绍过,聚类( Clustering \\textClustering Clustering)任务属于无监督学习( Unsupervised Learning \\textUnsupervised Learning Unsupervised Learning)任务。无监督学习任务的特点是:样本标签是未知的。而无监督学习的目标是通过学习无标签的样本来揭示数据的内在性质及规律。
而聚类试图将数据集内的样本划分为若干个子集,每个子集称为一个簇( Cluster \\textCluster Cluster)。从概率/非概率模型的角度划分,概率模型的典型模型是高斯混合模型;而非概率的聚类模型,其主要代表是 k k k均值算法( k-Means \\textk-Means k-Means)。
距离计算
在介绍 k-Means \\textk-Means k-Means算法之前,需要介绍聚类的有效性指标( Vaildity Index \\textVaildity Index Vaildity Index)。从直观上描述,在聚类的过程我们更希望物以类聚——相同簇的样本尽可能地彼此相似,不同簇的样本尽可能地不同。
对于两个样本点,通常使用计算它们在样本空间中的距离 来描述两样本之间的相似性程度。样本之间距离越小,样本之间的相似性程度越高,反之同理。
已知两个样本
x
(
i
)
,
x
(
j
)
x^(i),x^(j)
x(i),x(j)表示如下:
它们均属于
p
p
p维特征空间,即
x
(
i
)
,
x
(
j
)
∈
R
p
x^(i),x^(j) \\in \\mathbb R^p
x(i),x(j)∈Rp.
x
(
i
)
=
(
x
1
(
i
)
,
x
2
(
i
)
,
⋯
,
x
p
(
i
)
)
T
x
(
j
)
=
(
x
1
(
j
)
,
x
2
(
j
)
,
⋯
,
x
p
(
j
)
)
T
\\begincases x^(i) = \\left(x_1^(i),x_2^(i),\\cdots,x_p^(i)\\right)^T \\\\ x^(j) = \\left(x_1^(j),x_2^(j),\\cdots,x_p^(j)\\right)^T \\endcases
⎩
⎨
⎧x(i)=(x1(i),x2(i),⋯,xp(i))Tx(j)=(x1(j),x2(j),⋯,xp(j))T
关于描述样本
x
(
i
)
,
x
(
j
)
x^(i),x^(j)
x(i),x(j)之间的距离,最常用的方法是明可夫斯基距离(
Minkowski Distance
\\textMinkowski Distance
Minkowski Distance):
其中参数
m
≥
1
m \\geq 1
m≥1.
Dist
mk
(
x
(
i
)
,
x
(
j
)
)
=
(
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
m
)
1
m
\\textDist_\\textmk(x^(i),x^(j)) = \\left(\\sum_k=1^p \\left|x_k^(i) - x_k^(j)\\right|^m\\right)^\\frac1m
Distmk(x(