粒子群算法 | 启发式优化算法

Posted 2023-04-06 小云从0学算法

粒子群优化PSO

1、粒子群算法背景（PSO）

受到鸟群捕食启发。是一种群体智能算法，利用群体中的个体对信息的共享，

2、算法流程

粒子群算法的具体流程包括以下步骤：

1. 初始化粒子群：
   随机生成一系列具有随机速度和位置的粒子，同时记录每个粒子的个体历史最优位置和全局历史最优位置。

2. 粒子更新：
   根据当前的位置和速度、个体历史最优位置及全局历史最优位置等信息，计算粒子的新速度和新位置。速度改变的大小受到加速度限制器和阻力因子等限制。

   具体公式如下：

   for i=1 to 粒子数目 do

   ①.计算适应度值f(x_i)

   ②.更新粒子速度v_i和位置x_i

   v_i(k+1)=wv_i(k)+c1r1(x_pbesti(k)-x_i(k))+c2r2(x_gbest(k)-x_i(k))
   
   x_i(k+1)=x_i(k)+v_i(k+1)
   

   end for

   其中，v_i(k)为第i个粒子在第k次迭代时的速度，x_i(k)为第i个粒子在第k次迭代时的位置，x_pbesti(k)为第i个粒子在第k次迭代中所取得的最优位置，x_gbest(k)为全局历史最优位置，w、c1、c2为权值系数，r1、r2为随机数。

3. 评价粒子群：
   对所有粒子根据其新位置计算适应度值，并更新个体历史最优位置和全局历史最优位置。

4. 终止条件判断：
   如果达到预定的终止条件，例如满足最大迭代次数或者预设的目标值时，结束迭代并输出结果。否则，继续进行迭代，回到步骤2。

通过不断的迭代，粒子将逐渐聚集在全局最优解附近，最终得出最优解。

3、python实现

在粒子群算法中，c1和c2被称为加速常数，它们是控制粒子运动的参数。c1和c2通常被设置为常数，在算法中保持不变。c1和c2的作用是控制粒子在搜索空间中移动的速度和方向。

c1和c2的具体定义如下：

• c1：粒子本身的历史最佳位置和当前位置的差值的权重， 表示粒子的认知因子。
• c2：粒子所在的群体历史最佳位置和当前位置的差值的权重，表示粒子与群体的社会因子。

particles什么意思

在粒子群算法中，particles指的是粒子的集合，也可以称为粒子群。在算法执行过程中，每个粒子都代表着问题空间中的一个可能解，而particles则代表着粒子群的集合。
每个粒子都有自己的位置和速度，通过更新位置和速度，粒子可以移动到新的位置，以期望找到更优秀的解决方案。粒子群中的所有粒子都是同时更新的，他们通过彼此之间的交换信息来实现全局搜索。

全局最佳位置（gbest）&历史最佳位置（pbest）

在粒子群算法中，每个粒子都有自己的历史最佳位置（pbest）和全局最佳位置（gbest）。

• 自身历史最佳位置是指当前粒子已知的它自己达到的最优位置，即粒子在搜索过程中达到的最佳解。每个粒子通过比较自己历史上所到达的最佳位置和当前位置，来更新自身历史最佳位置。每个粒子都会记录自己的历史最佳位置，以便在后续迭代过程中进行比较和更新。

• 全局最佳位置是指整个粒子群已知的所有粒子中，目前达到的最优位置。在算法开始时，通常会将第一个粒子视为全局最佳位置，然后在迭代过程中，通过比较每个粒子的自身历史最佳位置和当前全局最佳位置，来更新全局最佳位置。所有的粒子共享同一个全局最佳位置，以便在算法迭代的过程中，能够更好地指导粒子的搜索方向，帮助其更快地达到最优解。

# 实现，你可以借此更好地理解如何在粒子群算法中应用
# VRP：
#
# ```python
import random


class Particle:
    def __init__(self, vrp, position):
        self.vrp = vrp
        self.position = position
        self.velocity = self.__initialize_velocity()  # 初始化时速度为0
        self.pbest = self.position  # 初始最优解为当前位置
        self.pbest_cost = self.__evaluate(self.pbest)  # 记录初始最优解的cost
        self.gbest = None
        self.gbest_cost = float('inf')

    def __initialize_velocity(self):
        velocity = []
        for i in range(len(self.vrp.customers)):
            velocity.append(random.uniform(-1, 1))  # 初始化速度范围为-1到1
        return velocity

    def __evaluate(self, solution):
        # 计算当前解的cost
        cost = 0
        for route in solution:
            demand = 0
            route_cost = 0
            if isinstance(route, int):
                route = [route]
            for customer in route:
                demand += self.vrp.customers[customer][1]
                route_cost += self.vrp.distance_matrix[customer][route[-1]]  # 路径长度 = 客户距离 + 已经服务的客户到仓库的距离
            route_cost += self.vrp.distance_matrix[0][route[0]]  # 起点到第一个客户距离
            route_cost += self.vrp.distance_matrix[0][route[-1]]  # 最后一个客户到仓库距离
            if demand > self.vrp.vehicle_capacity:
                route_cost += self.vrp.penalty * (demand - self.vrp.vehicle_capacity)
            cost += route_cost
        return cost

    def update_velocity(self, w, c1, c2, gbest_position):
        # 更新速度
        # 先判断 gbest_position 和 pbest 是否为 None
        if not gbest_position:
            return
        if not self.position or not self.pbest:
            return
        velocity_length = len(self.velocity)
        position_length = len(self.position)
        pbest_length = len(self.pbest)
        gbest_position_length = len(gbest_position)

        if velocity_length != position_length or velocity_length != pbest_length or velocity_length != gbest_position_length:
            return
        for i in range(len(self.velocity)):
            r1 = random.uniform(0, 1)
            r2 = random.uniform(0, 1)
            cognitive = c1 * r1 * (self.pbest[i] - self.position[i])
            print("velocity:", self.velocity)
            print("pbest:", self.pbest)
            print("position:", self.position)
            print("gbest_position:", gbest_position)
            social = c2 * r2 * (gbest_position[i] - self.position[i])
            self.velocity[i] = w * self.velocity[i] + cognitive + social

    def update_position(self):
        # 根据新速度更新当前位置
        if not self.position:  # 如果 self.position 列表为空，则不进行更新操作
            return
        new_position = []
        for i in range(len(self.vrp.customers)):
            if i >= len(self.position):  # 检查 i 是否超出了 self.position 的长度
                break
            if self.position[i] == 0:
                continue
            new_pos = self.position[i] + self.velocity[i]
            if new_pos < 1:
                new_pos = 1
            elif new_pos > len(self.vrp.customers) - 1:
                new_pos = len(self.vrp.customers) - 1
            new_position.append(int(new_pos))
        self.position = new_position

    def update_pbest(self):
        # 如果当前位置比已知最优解更好，则更新最优解
        new_cost = self.__evaluate(self.position)
        if new_cost < self.pbest_cost:
            self.pbest = self.position
            self.pbest_cost = new_cost

    def update_gbest(self, gbest_position, gbest_cost):
        # 更新全局最优解
        if gbest_cost < self.gbest_cost:
            self.gbest = gbest_position
            self.gbest_cost = gbest_cost


class VRP:
    def __init__(self, distance_matrix, customers, num_vehicles, vehicle_capacity, max_iterations=100, penalty=1000,
                 w=0.8, c1=0.5, c2=0.5, swarm_size=50):
        self.distance_matrix = distance_matrix
        self.customers = customers
        self.num_vehicles = num_vehicles
        self.vehicle_capacity = vehicle_capacity
        self.max_iterations = max_iterations
        self.penalty = penalty
        self.w = w
        self.c1 = c1 #什么意思
        self.c2 = c2
        self.swarm_size = swarm_size

    def solve(self):
        particles = [Particle(self, self.__initialize_particle()) for i in range(self.swarm_size)]
        gbest = None
        gbest_cost = float('inf')

        for i in range(self.max_iterations):
            for particle in particles:
                particle.update_velocity(self.w, self.c1, self.c2, gbest)
                particle.update_position()
                particle.update_pbest()
                if particle.pbest_cost < gbest_cost:
                    gbest = particle.pbest
                    gbest_cost = particle.pbest_cost
                particle.update_gbest(gbest, gbest_cost)
        return gbest, gbest_cost

    def __initialize_particle(self):
        # 初始化一个解
        customers = list(range(1, len(self.customers)))
        random.shuffle(customers)
        routes = []
        for i in range(self.num_vehicles):
            route = []
            remaining_capacity = self.vehicle_capacity
            for j in customers:
                if remaining_capacity >= self.customers[j][1]:
                    route.append(j)
                    remaining_capacity -= self.customers[j][1]
            routes.append(route)
        return [0] + sum(routes, []) + [0] * (len(self.customers) - len(sum(routes, [])))

# ```
#
# 然后你可以创建一个
# VRP
# 对象，并调用
# solve()
# 方法来解决问题：
#
# ```python
distance_matrix = [
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
]
customers = [
    (0, 0),
    (1, 10),
    (2, 15),
    (3, 20)
]
vrp = VRP(distance_matrix, customers, num_vehicles=2, vehicle_capacity=30)
solution, cost = vrp.solve()
print("Solution: ", solution)
print("Cost: ", cost)
# ```
#
# 以上仅为一个简单实现，仍可进行参数调优以得到更好的结果。

优化求解基于tent混沌改进粒子群优化算法

2.1 粒子群算法思想的起源

      粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法，自然界中各种生物体均具有一定的群体行为，而人工生命的主要研究领域之一是探索自然界生物的群体行为，从而在计算机上构建其群体模型。自然界中的鸟群和鱼群的群体行为一直是科学家的研究兴趣，生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型，在他的仿真中，每一个个体遵循：

      (1) 避免与邻域个体相冲撞；

      (2) 匹配邻域个体的速度；

      (3) 飞向鸟群中心，且整个群体飞向目标。

      仿真中仅利用上面三条简单的规则，就可以非常接近的模拟出鸟群飞行的现象。1995年，美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出了粒子群算法，其基本思想是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正，以使粒子飞向解空间并在最好解处降落。Kennedy在他的书中描述了粒子群算法思想的起源。

2.2 算法原理

     PSO从这种模型中得到启示并用于解决优化问题。PSO 中，每个优化问题的潜在解都是搜索空间中的一只鸟，称之为粒子。所有的粒子都有一个由被优化的函数决定的适值( fitness value) ，每个粒子还有一个速度决定它们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己；第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。

    假设在一个维的目标搜索空间中，有个粒子组成一个群落，其中第个粒子表示为一个维的向量

，。

     第个粒子的“飞行 ”速度也是一个维的向量，记为

，。

     第个粒子迄今为止搜索到的最优位置称为个体极值，记为

，。

     整个粒子群迄今为止搜索到的最优位置为全局极值，记为

      在找到这两个最优值时，粒子根据如下的公式(2-1)和( 2-2)来更新自己的速度和位置：

 (2-1)

 (2-2)

     其中：和为学习因子，也称加速常数(acceleration constant)，w为惯性因子，和为[0，1]范围内的均匀随机数。式(2-1)右边由三部分组成，第一部分为“惯性(inertia)”或“动量(momentum)”部分，反映了粒子的运动“习惯(habit)”，代表粒子有维持自己先前速度的趋势；第二部分为“认知(cognition)”部分，反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance)，代表粒子有向自身历史最佳位置逼近的趋势；第三部分为“社会(social)”部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体或邻域历史最佳位置逼近的趋势， ,是粒子的速度，，是常数，由用户设定用来限制粒子的速度。和是介于之间的随机数。

2.3 标准粒子群算法流程

    算法的流程如下：

     Step1:初始化粒子群，包括群体规模，每个粒子的位置和速度

     Step2:计算每个粒子的适应度值；

    Step3: 对每个粒子，用它的适应度值和个体极值比较，如果 ，则用替换掉；

    Step4: 对每个粒子，用它的适应度值和全局极值比较，如果则用替；

    Step5: 根据公式（2-1），（2-2）更新粒子的速度和位置 ；

    Step6: 如果满足结束条件(误差足够好或到达最大循环次数)退出，否则返回Step2。

图2-1. PSO算法流程图

%_________________________________________________________________________%
% 基于Tent混沌映射改进的粒子群优化算法             %
%_________________________________________________________________________%

% 使用方法
%__________________________________________
% fobj = @YourCostFunction        设定适应度函数
% dim = number of your variables   设定维度
% Max_iteration = maximum number of generations 设定最大迭代次数
% SearchAgents_no = number of search agents   种群数量
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n  变量下边界
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n   变量上边界
clear all
clc
close all
SearchAgents_no=10; % 种群数量
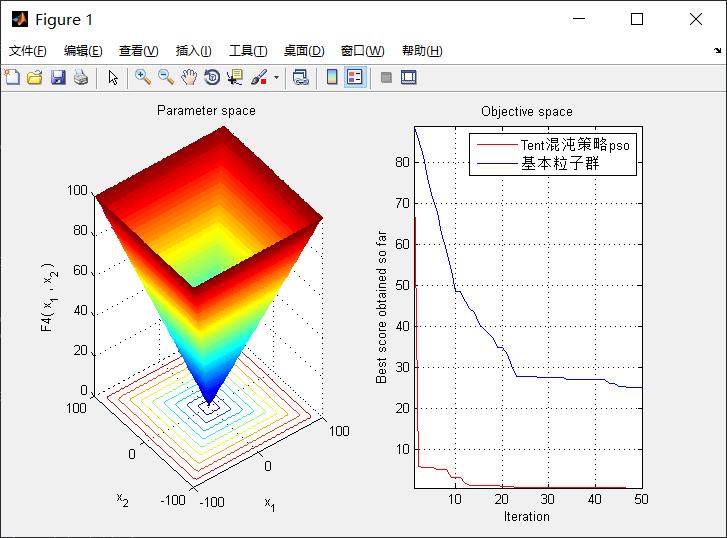
Function_name='F4'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper) 设定适应度函数
Vmax=5;%速度上限
Vmin=-5;%速度下限
Max_iteration=50;% 进化次数
a=0.5;%混沌系数
c1 = 1.49445;%个体学习率
c2 = 1.49445;%群体学习率
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);  %设定边界以及优化函数
%lb%粒子最小值
%ub%粒子最大值
%dim%粒子维数
[Best_pos_tent,pso_curve_tent,Best_score_tent]=psoNew(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Vmax,Vmin,a,c1,c2); %tent混沌粒子群
[Best_pos,pso_curve,Best_score]=pso(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Vmax,Vmin,c1,c2); %基本粒子群

figure('Position',[269   240   660   290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])

%Draw objective space
subplot(1,2,2);
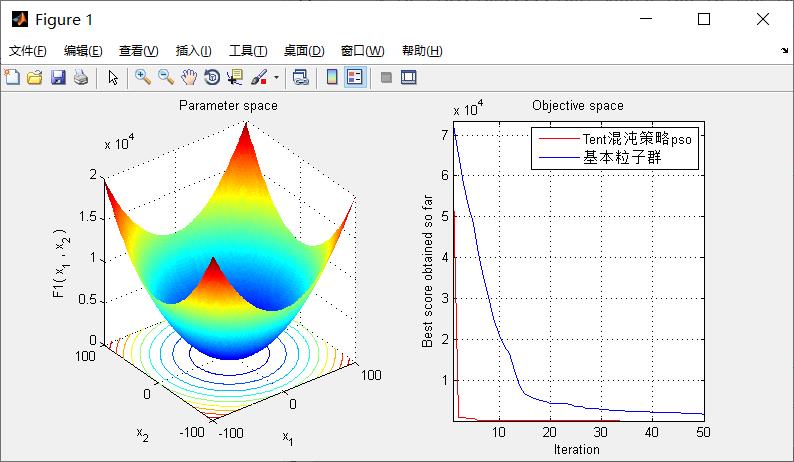
plot(pso_curve_tent,'Color','r')
hold on;
plot(pso_curve,'Color','b')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');

axis tight
grid on
box on
legend('Tent混沌策略pso','基本粒子群')
%
display(['The best solution obtained by Tent混沌策略PSO is : ', num2str(Best_pos_tent)]);
display(['The best optimal value of the objective funciton found by Tent混沌策略PSO is : ', num2str(Best_score_tent)]);
display(['The best solution obtained by PSO is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by Tent混沌策略PSO is : ', num2str(Best_score)]);

​

完整代码或仿真咨询QQ1575304183