粒子群算法

Posted 2021-09-09 好奇小圈

粒子群算法

1.入门

粒子群算法，其全称为粒子群优化算法(Particle Swarm Optimization,PsO)。它是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的搜索算法。

2.什么是启发式算法？

启发式算法百度百科上的定义:一个基于直观或经验构造的算法,在可接受的花费下给出待解决优化问题的一个可行解。
(1)什么是可接受的花费?
计算时间和空间能接受（求解一个问题要几万年or一万台电脑)
(2)什么是优化问题?
工程设计中优化问题(optimization problem)指在一定约束条件下,求解一个目标函数的最大值(或最小值)问题。
注:实际上和我们之前学过的规划问题的定义一样，称呼不同而已。
(3)什么是可行解?
得到的结果能用于工程实践(不一定非要是最优解)
常见的启发式算法:
粒子群、模拟退火、遗传算法、蚁群算法、禁忌搜索算法等等

3.什么是盲目搜索？

如枚举法、蒙特卡洛模拟
有什么问题?
如果现在要求最值的函数是一个多变量的函数，例如是一个10个变量的函数，那么就完蛋了!(要考虑的情况随着变量数呈指数增长，计算时间肯定不够)

4.启发式搜索-爬山法

以最简单的连续—元函数找最大值为例，我们来讲解爬山法:
(1在解空间中随机生成一个初始解;
(2)根据初始解的位置，我们在下一步有两种走法:向左邻域走一步或者向右邻
域走一步（走的步长越小越好,但会加大计算量);
(3)比较不同走法下目标函数的大小，并决定下一步往哪个方向走。上图中向左
走目标函数较大，因此我们应该往左走一小步;
(4)不断重复这个步骤，直到找到一个极大值点(或定义域边缘处)．此时我们就
结束搜索。

粒子群算法基础概念

来源

1995年，美国学者Kennedy和Eberhart共同提出了粒子群算法,其基本思想源于对鸟类群体行为进行建模与仿真的研究结果的启发。

核心思想

它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。

最初提出的论文:

Kennedy J , Eberhart R .Particle swarm optimization[C]// Proceedings of lICNN’95 - International Conference on Neural Networks.IEEE, 1995.

图形解释

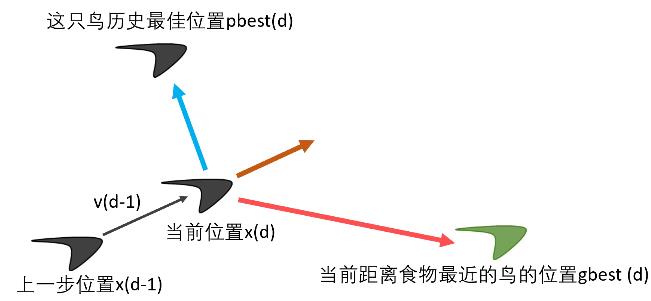
这只鸟第d步所在的位置=第d-1步所在的位置＋第d-1步的速度运动的时间
x(d)= x(d-1) + v(d-1) ×t(每一步运动的时间t—般取1)

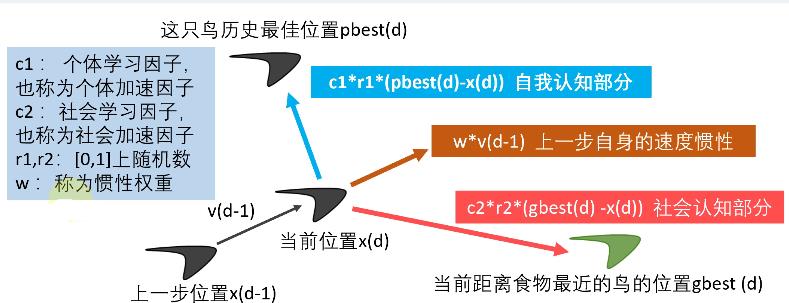
这只鸟第d步所在的位置=第d-1步所在的位置＋第d-1步的速度运动的时间
x(d) = x(d-1) + v(d-1) ×t(每一步运动的时间t—般取1)
这只鸟第d步的速度=上一步自身的速度惯性＋自我认知部分+社会认知部分
v(d) = w×v(d-1) + c1×r1×(pbest(d)-x(d)) + c2×r2×(gbest(d)-x(d))(三个部分的和)

一些概念

粒子:优化问题的候选解
位置:候选解所在的位置
速度:候选解移动的速度
适应度:评价粒子优劣的值，一般设置为目标函数值
**个体最佳位置:**单个粒子迄今为止找到的最佳位置
群体最佳位置:所有粒子迄今为止找到的最佳位置

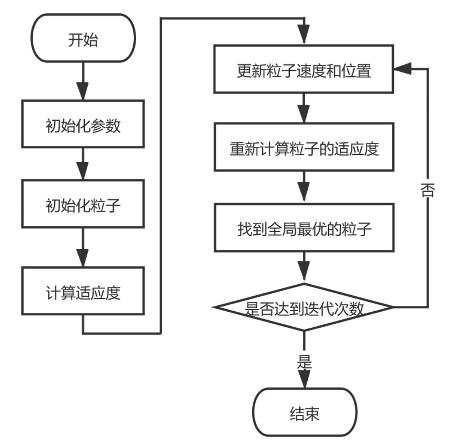
流程图

符号说明

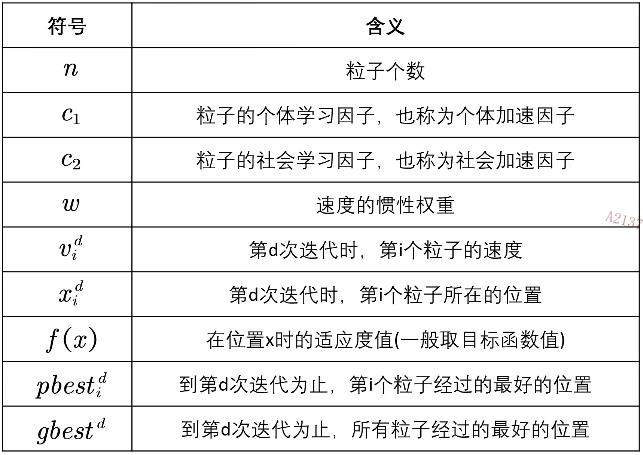
核心公式

这只鸟第d步所在的位置=第d-1步所在的位置＋第d-1步的速度*运动的时间
x(d) = x(d-1) + v(d-1) ×t(每一步运动的时间t—般取1)

这只鸟第d步的速度=上一步自身的速度惯性＋自我认知部分+社会认知部分
v(d) = w×v(d-1) + c1×r1×(pbest(d)-x(d)) + c2×r2×(gbest(d)-x(d))(三个部分的和)

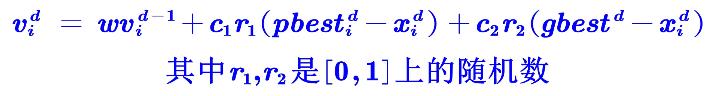
因数确定

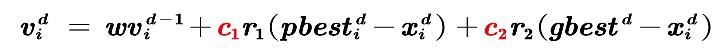
在最初提出粒子群算法的论文中指出，个体学习因子和社会(或群体)学习因子取2比较合适。
(注意:最初提出粒子群算法的这篇论文没有惯性权重)

Kennedy J , Eberhart R .Particle swarm optimization[C]// Proceedings of lICNN’95 - International Conference on Neural Networks.IEEE, 1995.

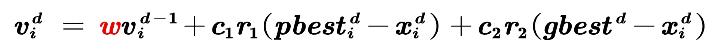
论文中得到的结论:惯性权重取0.9-1.2是比较合适的,一般取0.9就行
引入惯性权重的论文:

SHI,Y. A Modified Particle Swarm Optimizer[C]// Proc. of IEEE ICEC conference, Anchorage.1998.

粒子群算法代码实现（MATLAB）

例题

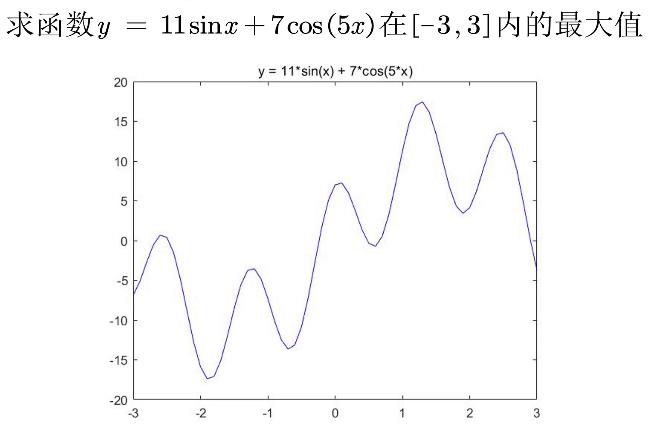
初始化参数

n=10;%粒子数量
narvs = 1; %变量个数(函数中有几个自变量)
c1 = 2; %每个粒子的个体学习因子
c2 = 2; %每个粒子的社会学习因子
w = 0.9;%惯性权重
K = 50;%迭代的次数
vmax = 1.2; %粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界

(1)增加粒子数量会增加我们找到更好结果的可能性，但会增加运算的时间。
(2) c1,c2,w这三个量有很多改进空间，未来我再来专门讲怎么去调整。
(3)迭代的次数K越大越好吗?不一定哦．如果现在已经找到最优解了，再增加迭代次数是没有意义的。
(4)这里出现了粒子的最大速度、是为了保证下一步的位置离当前位置别太远，—般取自变量可行域的10%至20%(不同文献看法不同)。
(5)X的下界和上界是保证粒子不会飞出定义域。

初始化粒子

x= zeros(n,narvs);
for i = 1: narvs
%随机初始化粒子所在的位置在定义域内
x(:,i) = x_lb(0) + (x_ub(i)-x_lb(i))*rand(n,1);
end
%随机初始化粒子的速度，设置为[-vmax,vmax]
v= -vmax + 2*vmax .* rand(n,narvs);

(1)这里为什么要写成下标的形式?
保证程序的兼容性,“适配"多元函数
(2)行向量为什么可以和矩阵来点乘?

(3)行向量为什么可以和矩阵来相加?

计算适应度

fit = zeros(n,1);%初始化这n个粒子的适应度全为0
for i = 1:n %循环整个粒子群,计算每一个粒子的适应度
fit(i) = Obj_fun1(x(i,:));%调用Obj_fun1函数来计算适应度(这里写成x讷)主要是为了和以后遇到的多元函数互通)
end
pbest = x;%初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == max(fit),1);%找到适应度最大的那个粒子的下标
gbest = x(ind,:);%定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量)

注意:
(1)这里的适应度实际上就是我们的目标函数值。
(2)这里可以直接计算出pbest和gbest,在后面将用于计算粒子的速度以更新粒子的位置。

更新粒子速度和位置循环

for d=1:K%开始迭代，一共迭代K次
   for i=1:n%依次更新第i个粒子的速度与位置
        %更新第i个粒子的速度
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:))+ c2*rand(1)*(gbest - x(i,:));

        %如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); %更新第i个粒子的位置
        %如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
           fit(i)= Obj_fun1(x(i,:));%重新计算第i个粒子的适应度
        %如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
        if fit(i) > Obj_fun1(pbest(i,:))
        pbest(i,:)=x(i,:);%那就更新第i个粒子迄今为止找到的最佳位置
        end
        %如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
        if Obj_fun1(pbest(i,:)) > Obj_fun1(gbest)
        gbest =pbest(i,:);%那就更新所有粒子迄今为止找到的最佳位置
        end
   end    
end

图形绘制

绘制函数的图形

x= -3:0.01:3;
y = 11*sin(x) + 7*cos(5*x);figure(1)
plot(x,y,'b-')
title('y = 11*sin(x)+ 7*cos(5*x)')
hold on

代码汇总

    clear;clc;
    x= -3:0.01:3;
	y = 11*sin(x) + 7*cos(5*x);figure(1)
	plot(x,y,'b-')
	title('y = 11*sin(x)+ 7*cos(5*x)')
	hold on
    %%
    n=10;%粒子数量
    narvs = 1; %变量个数(函数中有几个自变量)
    c1 = 2; %每个粒子的个体学习因子
    c2 = 2; %每个粒子的社会学习因子
    w = 0.9;%惯性权重
    K = 50;%迭代的次数
    vmax = 1.2; %粒子的最大速度
    x_lb = -3; % x的下界
    x_ub = 3; % x的上界

    %%
    x= zeros(n,narvs);
    for i = 1: narvs
    %随机初始化粒子所在的位置在定义域内
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);
    end
    %随机初始化粒子的速度，设置为[-vmax,vmax]
    v= -vmax + 2*vmax .* rand(n,narvs);
    
    %%
    fit = zeros(n,1);%初始化这n个粒子的适应度全为0
    for i = 1:n %循环整个粒子群,计算每一个粒子的适应度
    fit(i) = Obj_fun1(x(i,:));%调用Obj_fun1函数来计算适应度(这里写成x讷)主要是为了和以后遇到的多元函数互通)
    end
    pbest = x;%初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
    ind = find(fit == max(fit),1);%找到适应度最大的那个粒子的下标
    gbest = x(ind,:);%定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量)
    
    %%
    h = scatter(x,fit,80,'*r');
    fitnessbest = ones(K,1);%初始化每次迭代得到的最佳的适应度
    for d=1:K%开始迭代，一共迭代K次
       for i=1:n%依次更新第i个粒子的速度与位置
            %更新第i个粒子的速度
            v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:))+ c2*rand(1)*(gbest - x(i,:));

            %如果粒子的速度超过了最大速度限制，就对其进行调整
            for j = 1: narvs
                if v(i,j) < -vmax(j)
                    v(i,j) = -vmax(j);
                elseif v(i,j) > vmax(j)
                    v(i,j) = vmax(j);
                end
            end
            x(i,:) = x(i,:) + v(i,:); %更新第i个粒子的位置
            %如果粒子的位置超出了定义域，就对其进行调整
            for j = 1: narvs
                if x(i,j) < x_lb(j)
                    x(i,j) = x_lb(j);
                elseif x(i,j) > x_ub(j)
                    x(i,j) = x_ub(j);
                end
            end
               fit(i)= Obj_fun1(x(i,:));%重新计算第i个粒子的适应度
            %如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            if fit(i) > Obj_fun1(pbest(i,:))
            pbest(i,:)=x(i,:);%那就更新第i个粒子迄今为止找到的最佳位置
            end
            %如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            if Obj_fun1(pbest(i,:)) > Obj_fun1(gbest)
            gbest =pbest(i,:);%那就更新所有粒子迄今为止找到的最佳位置
            end
           fitnessbest(d) = Obj_fun1(gbest);%更新第d次迭代得到的最佳的适应度
           pause(0.1)%暂停0.1s
           h.XData = x; %更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化)
           h.YData = fit; %更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化)

       end 
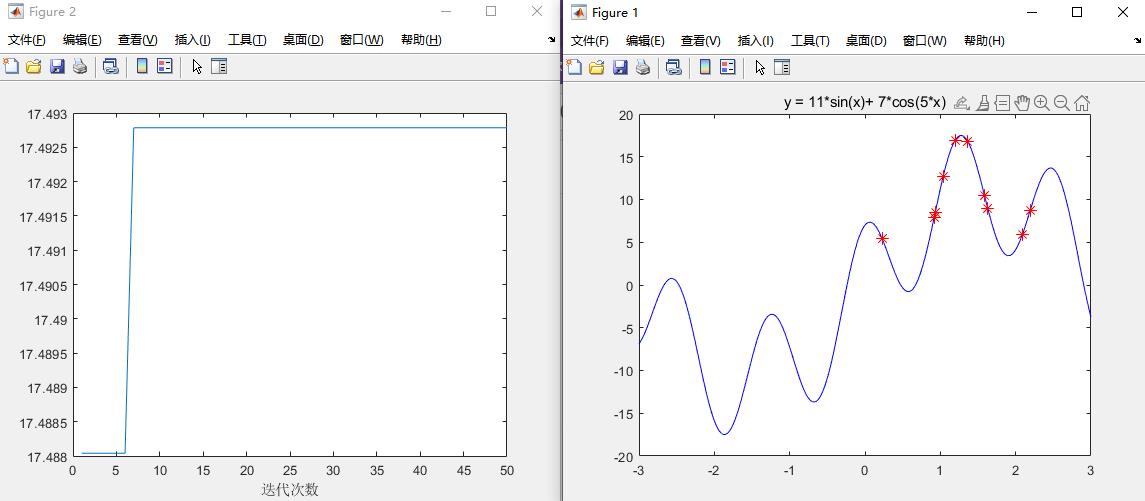
        figure(2)
        plot(fitnessbest)%绘制出每次迭代最佳适应度的变化图
        xlabel('迭代次数');
        disp('最佳的位置是:'); disp(gbest)
        disp('此时最优值是:'); disp(Obj_fun1(gbest))

    end