数学建模暑期集训18：粒子群算法

Posted 2021-09-05 Z|Star

粒子群算法属性

针对问题：复杂情况的优化问题
算法分类：启发式算法

粒子群算法的直观解释

通过鸟寻找食物的情景，可以对该更好理解该算法的基本公式。

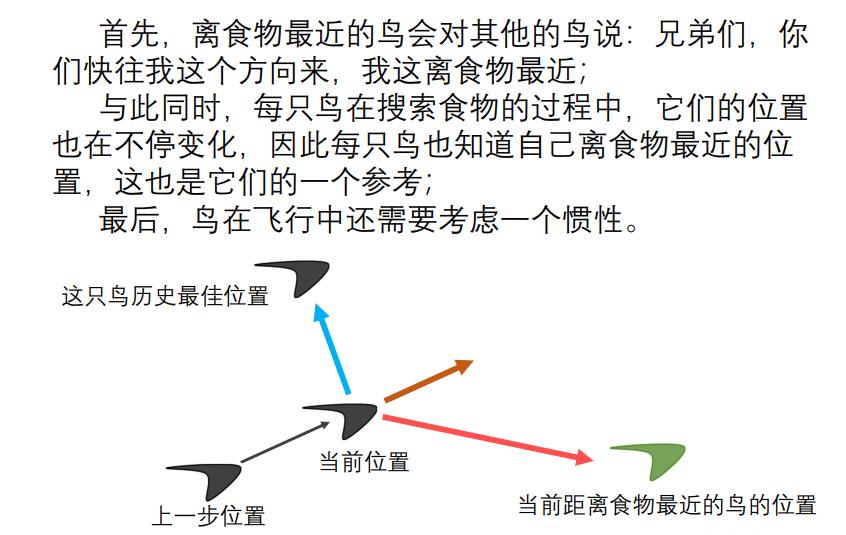
粒子群算法中的基本概念

粒子群算法流程图

符号说明

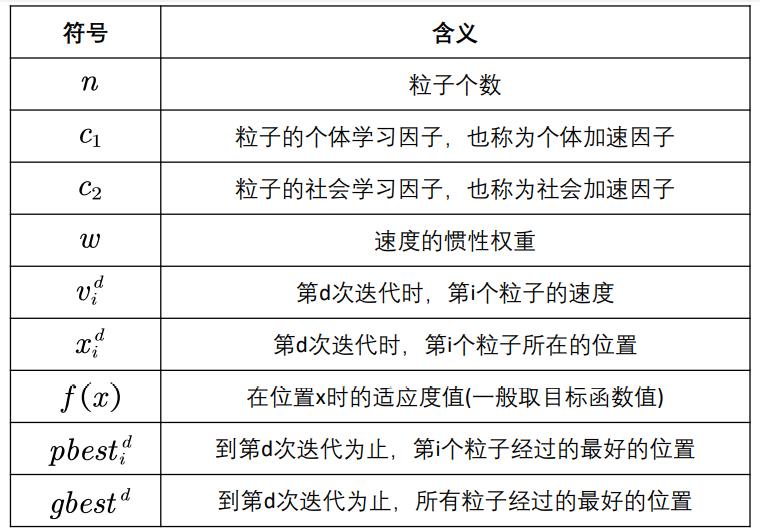
粒子群算法的核心公式

粒子群算法基本框架

下面将记录粒子群算法的框架和优化过程。
若要实际使用，可使用matlab自带的粒子群算法调用函数，详情见最后一节的使用案例。

初始化参数

n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 50;  % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界

初始化粒子

%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs);  % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）

计算适应度

%% 计算适应度
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun1(x(i,:));   % 调用Obj_fun1函数来计算适应度（这里写成x(i,:)主要是为了和以后遇到的多元函数互通）
end
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1);  % 找到适应度最大的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

Obj_fun1为自定义的目标函数

更新粒子速度和位置并计算适应度

%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun1(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) > Obj_fun1(pbest(i,:))   % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) > Obj_fun1(gbest)  % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun1(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x;  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = fit; % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
end

输出结果

figure(2)
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun1(gbest))

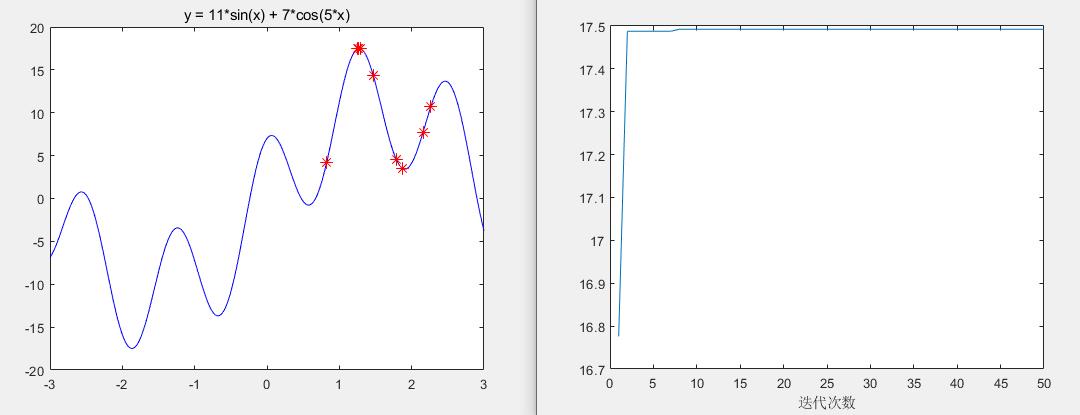
粒子群算法优化思路

非线性递减惯性权重

惯性递减除了线性的，也可以是非线性的。

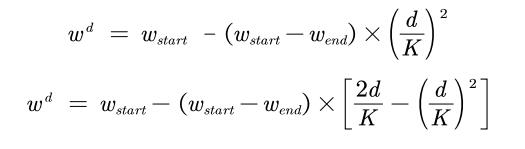
自适应惯性权重

随机惯性权重

使用随机的惯性权重，可以避免在迭代前期局部搜索能力的不足；也可以避免在迭代后期全局搜索能力的不足。

压缩(收缩)因子法

非对称学习因子

粒子群算法测试函数

测试函数用来检测算法的优劣。

使用matlab内置的粒子群算法

Matlab自带的粒子群函数 particleswarm
particleswarm函数是求最小值的
如果目标函数是求最大值则需要添加负号从而转换为求最小值

参数说明

使用案例与参数修改

%% 直接调用particleswarm函数进行求解测试函数
narvs = 30; % 变量个数
% Sphere函数
% x_lb = -100*ones(1,30); % x的下界
% x_ub = 100*ones(1,30); % x的上界
% Rosenbrock函数
x_lb = -30*ones(1,30); % x的下界
x_ub = 30*ones(1,30); % x的上界
% Rastrigin函数
% x_lb = -5.12*ones(1,30); % x的下界
% x_ub = 5.12*ones(1,30); % x的上界
% Griewank函数
% x_lb = -600*ones(1,30); % x的下界
% x_ub = 600*ones(1,30); % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub)  


%% 绘制最佳的函数值随迭代次数的变化图
options = optimoptions('particleswarm','PlotFcn','pswplotbestf')   
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 展示函数的迭代过程
options = optimoptions('particleswarm','Display','iter');
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 修改粒子数量，默认的是：min(100,10*nvars)
options = optimoptions('particleswarm','SwarmSize',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 在粒子群算法结束后继续调用其他函数进行混合求解（hybrid  n.混合物合成物; adj.混合的; 杂种的;） 
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 惯性权重的变化范围，默认的是0.1-1.1
options = optimoptions('particleswarm','InertiaRange',[0.2 1.2]);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 个体学习因子，默认的是1.49（压缩因子）
options = optimoptions('particleswarm','SelfAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 社会学习因子，默认的是1.49（压缩因子）
options = optimoptions('particleswarm','SocialAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 最大的迭代次数，默认的是200*nvars
options = optimoptions('particleswarm','MaxIterations',10000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 领域内粒子的比例 MinNeighborsFraction，默认是0.25 
options = optimoptions('particleswarm','MinNeighborsFraction',0.2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 函数容忍度FunctionTolerance, 默认1e-6, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','FunctionTolerance',1e-8);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 最大停滞迭代数MaxStallIterations, 默认20, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','MaxStallIterations',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)

%% 不考虑计算时间，同时修改三个控制迭代退出的参数
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',100000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc

%% 在粒子群结束后调用其他函数进行混合求解
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',50,'MaxIterations',20000,'HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc

粒子群算法实际案例

问题：求解方程组

调用内置粒子群函数求解：

function f = Obj_fun(x)
    f1= abs(x(1)+x(2))-abs(x(3)) ;
    f2 = x(1) * x(2) * x(3) + 18;
    f3= x(1)^2 * x(2) + 3*x(3);
    f = abs(f1) + abs(f2) + abs(f3);
end

clear; clc
narvs = 3;
% 使用粒子群算法，不需要指定初始值，只需要给定一个搜索的范围
lb = -10*ones(1,3);  ub = 10*ones(1,3);  
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',20000,'SwarmSize',100);
[x, fval] = particleswarm(@Obj_fun,narvs,lb,ub,options) 

注：存在多解情况，每次输出结果都不太一样。