模型降阶方法之张量方法应用举例

Posted 2022-08-06 陆嵩

模型降阶方法之张量方法应用举例

文章目录

• • 模型降阶方法之张量方法应用举例
  • • 序章
    • 热传导方程
    • • 方法
      • 数值结果
    • 对流扩散方程
    • • 方法
      • 数值结果

序章

POD 方法参考：
https://blog.csdn.net/lusongno1/article/details/125944587

DEIM 方法参考：
https://blog.csdn.net/lusongno1/article/details/125955245

张量方法参考：
https://blog.csdn.net/lusongno1/article/details/126013084

很多同学看完了张量方法表示，算法流程是 clear 的，但是并不知道怎么应用。这里举两个简单的例子，热传导方程和对流扩散方程。

我们可以看到，张量方法是应用于 ODEs 的，那么如果从 PDE 得到 ODEs 呢？简单地说， PDE 在空间上做离散，比如说有限元离散或者有限差分离散，那么就把问题转为了向量值 ODEs，就可以用 ROMs 方法去处理。 如果用的是有限元方法处理的，那么向量值解的每个分量其实就表示每个基函数前面的系数（自由度）。如果是用有限差分方法处理的，那么向量值解的每个分量其实就表示每个节点上的值。

下面我们考虑这两个例子。有一些符号的含义是显而易见的，所以就不多加解释了。

热传导方程

方法

考虑热传导方程，
$$w_t=\Delta w$$
它的边界条件是，
$${(\mathbf{n}\cdot \nabla w+q(\mathbf{x},\mathbf{\alpha })w)|}_{\partial \Omega }=g(\mathbf{x},\mathbf{\alpha })$$
其中，$\mathbf{\alpha }\in {\mathbb{R}}^4$ 是个四维的参数。这里的求解区域为长方形挖三个洞，

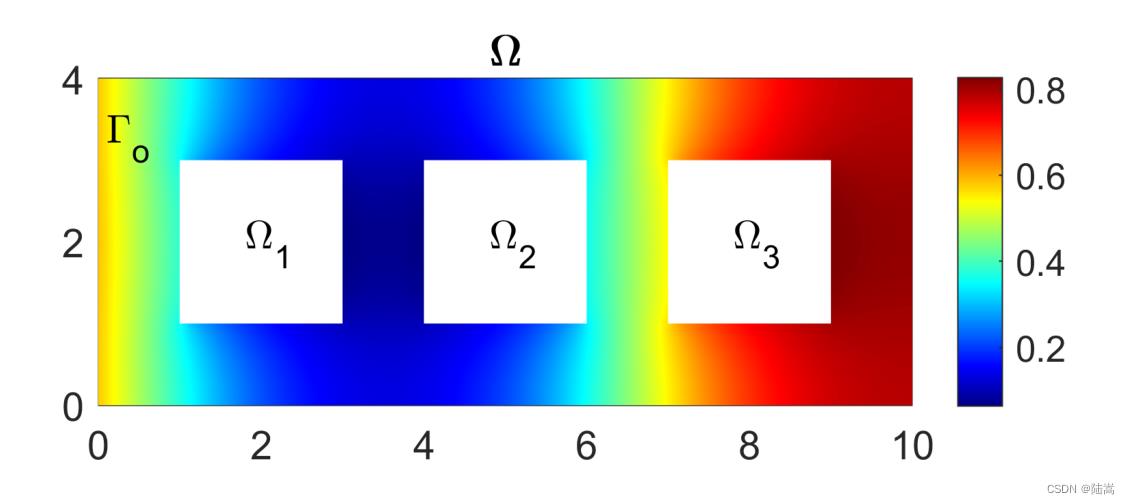
用标准的有限元方法，在空间上做离散，就得到这样一个时间连续的方程，
$$\mathrm{M}{\mathbf{u}}_t+(\mathrm{K}+\mathrm{Q}(\mathbf{\alpha }))\mathbf{u}=\mathbf{g}(\mathbf{\alpha })$$
其中，$M$ 是质量矩阵，$K$ 是刚度矩阵，
$$(\mathrm{Q}{)}_{ij}(\mathbf{\alpha })={\int }_{\partial \Omega }q(\mathbf{x},\mathbf{\alpha }){\theta }_j(\mathbf{x}){\theta }_i(\mathbf{x})d{s}_{\mathbf{x}},(\mathbf{g}{)}_j(\mathbf{\alpha })={\int }_{\partial \Omega }g(\mathbf{x},\mathbf{\alpha }){\theta }_j(\mathbf{x})d{s}_{\mathbf{x}},$$
那么，我们就可以将其写的 ODEs 的形式，
$${\mathbf{u}}_t=F(t,\mathbf{u},\mathbf{\alpha })$$
其中，
$$F(t,\mathbf{u},\mathbf{\alpha })=-{\mathrm{M}}^{-1}(\mathrm{K}+\mathrm{Q}(\mathbf{\alpha }))\mathbf{u}+{\mathrm{M}}^{-1}\mathbf{g}(\mathbf{\alpha })$$
有了这个，我们就可以用所谓的张量方法来寻求 reduced basis 了。首先，我们用 CN 格式得到一些快照，
$${\mathbf{\varphi }}_k=\mathbf{u}\left(t_k,\mathbf{\alpha }\right)$$
函数解事实上可由解向量表示出来，即
$$w\left(t_k,\mathbf{x},\mathbf{\alpha }\right)=\Theta (\mathbf{x})\mathbf{u}\left(t_k,\mathbf{\alpha }\right)$$
用之前提到的张量方法（不管是 CP、HOSVD 还是 TT），一波操作之后，我们便得到了一组 reduced 基，
$$\mathrm{Z}=\left[{\mathbf{z}}_1,\dots ,{\mathbf{z}}_n\right]\in {\mathbb{R}}^{M\times n}$$

不清楚怎么得到的，回看张量方法。事实上，$\mathrm{Z}={\mathrm{UU}}_c$，${\mathrm{U}}_c$ 取的是左奇异向量的前几列。

接着，类似于 POD 方法的投影方式，我们可以把这个方程投影到低阶的子空间中去做，得到
$$\tilde{\mathrm{M}}{\tilde{\mathbf{u}}}_t+(\tilde{\mathrm{K}}+\tilde{\mathrm{Q}}(\mathbf{\alpha }))\tilde{\mathbf{u}}=\tilde{\mathbf{g}}(\mathbf{\alpha })$$
其中，
M ~ = Z T M Z ∈ R n × n , K ~ = Z T K Z ∈ R n × n ,  Q ~ ( α ) = Z T Q ( α ) Z ∈ R n × n , g ~ ( α ) = Z T g ( α ) ∈ R n ,  \\beginaligned &\\widetilde\\mathrmM=\\mathrmZ^T \\mathrmMZ \\in \\mathbbR^n \\times n, \\quad \\widetilde\\mathrmK=\\mathrmZ^T \\mathrmKZ \\in \\mathbbR^n \\times n \\text , \\\\ &\\widetilde\\mathrmQ(\\boldsymbol\\alpha)=\\mathrmZ^T \\mathrmQ(\\boldsymbol\\alpha) \\mathrmZ \\in \\mathbbR^n \\times n, \\quad \\widetilde\\mathbfg(\\boldsymbol\\alpha)=\\mathrmZ^T \\mathbfg(\\boldsymbol\\alpha) \\in \\mathbbR^n \\text , \\endaligned ​M =ZTMZ∈Rn×n,K =ZTKZ∈Rn×n, Q ​(α)=ZTQ(α)Z∈Rn×n,模型降阶方法之张量方法

模型降阶方法之张量方法

模型降阶方法之 DEIM

模型降阶方法之 DEIM

模型降阶方法之 POD

模型降阶方法之 POD