傅里叶谱方法-傅里叶谱方法求解基本偏微分方程(一维波动方程 二维波动方程一维非线性薛定谔方程)及其Matlab程序实现

Posted 2023-04-01 图灵猫

3.2 傅里叶谱方法求解基本偏微分方程 (组)

3.2.1 一维波动方程

对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 $(-\infty <$

OpenCV 例程200篇232. 特征描述之频谱方法

『youcans 的 OpenCV 例程200篇 - 总目录』

【youcans 的 OpenCV 例程200篇】232. 纹理特征之频谱方法

4.3 纹理特征之频谱方法

傅里叶谱可以描述图像中的周期性或半周期性二维模式的方向性，因此可以基于傅里叶变换对纹理进行频谱分析。

纹理与图像频谱中的高频分量密切相关，纹理模式在频谱图表现为高能量的爆发。

傅里叶谱具有三个特征可以描述纹理的性质：

（1）傅里叶频谱中的突出峰值对应于纹理模式的主方向；
（2）频域图中的峰值位置对应于纹理模式在空间上的基本周期；
（3）通过滤波消除周期分量，用统计方法描述剩下的非周期性信号。

把傅里叶幅度谱转换到极坐标中表示为函数 $S(r,\theta )$，可以简化对频谱特性的解释。S 是频谱函数，r 和 $\theta$ 是极坐标系的半径和角度坐标轴。S 对于每一个方向 $\theta$ 可以简化为一维函数 $S_{\theta }(r)$；S 对于每一个半径 r 也可以简化为一维函数 $S_r(\theta )$。

分别对一维函数 $S_{\theta }(r)$ 和 $S_r(\theta )$ 积分，可以获得纹理频谱的全局描述：
$$\begin{gathered} S(r)=\sum _{\theta =0}^{\pi }{S}_{\theta }(r) \\ S(\theta )=\sum _{r=1}^R{S}_r(\theta ) \end{gathered}$$
如果纹理具有空间的周期性或确定的方向性，则一维函数 $S(r)$ 和 $S(\theta )$ 在对应的频率具有峰值。

例程 14.13：特征描述之傅里叶频谱纹理分析

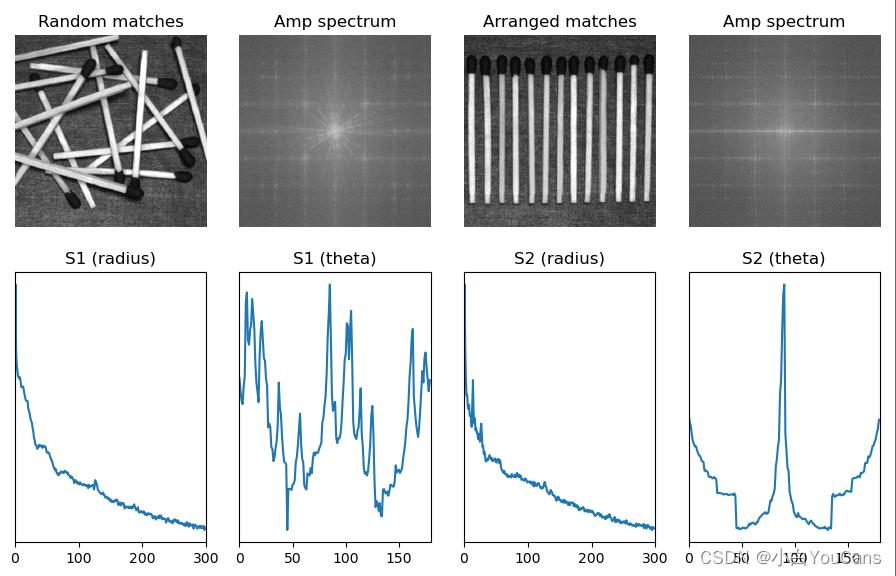
本例选自冈萨雷斯《数字图像处理（第四版）》P617 例11.14。一幅包含随机分布目标的图像和另一幅周期性排列目标的图像，在傅里叶变换的幅度谱具有不同的表现形式。

对于随机摆放和整齐摆放的物体图像，使用傅里叶频谱可以显示不同的图像，但直接分析频谱图像比较困难。将其转换到极坐标系中，用一维函数 $S(r)$ 和 $S(\theta )$ 表示就非常直观。

对于随机摆放的火柴图像，函数 $S(r)$ 曲线没有很强的周期分量；而对于整齐摆放的火柴图像，函数 $S(r)$ 曲线在r=15、r=25 附近具有很强的峰值，对应于频谱图中的亮区域的周期性水平重复。类似地，随机摆放火柴图像的$S_r(\theta )$ 曲线的分布混乱没有显著的峰值，而在整齐摆放的火柴图像中，$S_r(\theta )$ 曲线在 $\theta =90^o$ 具有非常强烈的能量峰值，对应于频谱图中的水平方向的能量爆发。

    # 14.13 特征描述之纹理谱分析
    def halfcircle(radius, x0, y0):  # 计算圆心(x0,y0) 半径为 r 的半圆的整数坐标
        degree = np.arange(180, 360, 1)  # 因对称性可以用半圆 (180,)
        theta = np.float32(degree * np.pi / 180)  # 弧度，一维数组 (180,)
        xc = (x0 + radius * np.cos(theta)).astype(np.int)  # 计算直角坐标，整数
        yc = (y0 + radius * np.sin(theta)).astype(np.int)
        return xc, yc

    def intline(x1, x2, y1, y2):  # 计算从(x1,y1)到(x2,y2)的线段上所有点的坐标
        dx, dy = np.abs(x2-x1), np.abs(y2-y1)  # x, y 的增量
        if dx==0 and dy==0:
            x, y = np.array([x1]), np.array([y1])
            return x, y
        if dx > dy:
            if x1>x2:
                x1, x2 = x2, x1
                y1, y2 = y2, y1
            m = (y2-y1) / (x2-x1)
            x = np.arange(x1, x2+1, 1)  #[x1,x2]
            y = (y1 + m*(x-x1)).astype(np.int)
        else:
            if y1>y2:
                x1, x2 = x2, x1
                y1, y2 = y2, y1
            m = (x2-x1) / (y2-y1)
            y = np.arange(y1, y2+1, 1)  # [y1,y2]
            x = (x1 + m*(y-y1)).astype(np.int)
        return x, y

    def specxture(gray):
        # cv2.dft 实现图像的傅里叶变换
        height, width = gray.shape
        x0, y0 = int(height / 2), int(width / 2)  # x0=300, y0=300
        rmax = min(height, width) // 2 - 1  # rmax=299
        print(height, width, x0, y0, rmax)
        # FFT 变换 （youcans）
        gray32 = np.float32(gray)  # 将图像转换成 float32
        dft = cv2.dft(gray32, flags=cv2.DFT_COMPLEX_OUTPUT)  # 傅里叶变换，(600, 600, 2)
        dftShift = np.fft.fftshift(dft)  # 将低频分量移动到频域图像的中心
        sAmp = cv2.magnitude(dftShift[:, :, 0], dftShift[:, :, 1])  # 幅度谱，中心化 (600, 600)
        sAmpLog = np.log10(1 + np.abs(sAmp))  # 幅度谱对数变换 (600, 600)
        # FFT 频谱沿半径的分布函数
        sRad = np.zeros((rmax,))  # (299,)
        sRad[0] = sAmp[x0, y0]
        for r in range(1, rmax):
            xc, yc = halfcircle(r, x0, y0)  # 半径为 r 的圆的整数坐标 (360,)
            sRad[r] = sum(sAmp[xc[i], yc[i]] for i in range(xc.shape[0]))  # (360,)
        sRadLog = np.log10(1 + np.abs(sRad))  # 极坐标幅度谱 youcans 对数变换
        # FFT 频谱沿角度的分布函数
        xmax, ymax = halfcircle(rmax, x0, y0)  # 半径为 xupt 的圆的整数坐标 (360,)
        sAng = np.zeros((xmax.shape[0],))  # (360,)
        for a in range(xmax.shape[0]):  # xmax.shape[0]=(360,)
            xr, yr = intline(x0, xmax[a], y0, ymax[a])  # 从(x0,y0)到(xa,ya)线段所有点的坐标 (300,)
            sAng[a] = sum(sAmp[xr[i], yr[i]] for i in range(xr.shape[0]))  # (360,)
        return sAmpLog, sRadLog, sAng

    # 纹理的傅里叶频谱分析
    gray1 = cv2.imread("../images/Fig1135a.tif", flags=0)  # flags=0 读取为灰度图像
    gray2 = cv2.imread("../images/Fig1135b.tif", flags=0)

    sAmpLog1, sRadLog1, sAng1 = specxture(gray1)  # 图像纹理的频谱分析
    sAmpLog2, sRadLog2, sAng2 = specxture(gray2)
    print(sAmpLog1.shape, sRadLog1.shape, sAng1.shape)

    plt.figure(figsize=(9, 6))
    plt.subplot(241), plt.axis('off'), plt.title("Random matches"), plt.imshow(gray1, 'gray')
    plt.subplot(242), plt.axis('off'), plt.title("Amp spectrum"), plt.imshow(sAmpLog1, 'gray')
    plt.subplot(243), plt.axis('off'), plt.title("Arranged matches"), plt.imshow(gray2, 'gray')
    plt.subplot(244), plt.axis('off'), plt.title("Amp spectrum"), plt.imshow(sAmpLog2, 'gray')
    plt.subplot(245), plt.plot(sRadLog1), plt.title("S1 (radius)"), plt.xlim(0,300), plt.yticks([])
    plt.subplot(246), plt.plot(sAng1), plt.title("S1 (theta)"), plt.xlim(0,180), plt.yticks([])
    plt.subplot(247), plt.plot(sRadLog2), plt.title("S2 (radius)"), plt.xlim(0,300), plt.yticks([])
    plt.subplot(248), plt.plot(sAng2), plt.title("S2 (theta)"), plt.xlim(0,180), plt.yticks([])
    plt.tight_layout()
    plt.show()

【本节完】

版权声明：
youcans@xupt 原创作品，转载必须标注原文链接：(https://blog.csdn.net/youcans/article/details/125704655)
Copyright 2022 youcans, XUPT
Crated：2022-7-10

231. 特征描述之 灰度共生矩阵（GLCM）