相关性分析matlab spss excel 哪个最好
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了相关性分析matlab spss excel 哪个最好相关的知识,希望对你有一定的参考价值。
相较而言,SPSS应该更好,SPSS是专业的统计软件,Matlab更倾向于科学计算与开发,Excel则面向日常的数据处理。SPSS(Statistical Product and Service Solutions),“统计产品与服务解决方案”软件。最初软件全称为“社会科学统计软件包”(SolutionsStatistical Package for the Social Sciences),但是随着SPSS产品服务领域的扩大和服务深度的增加,SPSS公司已于2000年正式将英文全称更改为“统计产品与服务解决方案”,标志着SPSS的战略方向正在做出重大调整。为IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品及相关服务的总称SPSS,有Windows和Mac OS X等版本。SPSS for Windows是一个组合式软件包,它集数据录入、整理、分析功能于一身。用户可以根据实际需要和计算机的功能选择模块,以降低对系统硬盘容量的要求,有利于该软件的推广应用。SPSS的基本功能包括数据管理、统计分析、图表分析、输出管理等等。SPSS统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类,每类中又分好几个统计过程,比如回归分析中又分线性回归分析、曲线估计、Logistic回归、Probit回归、加权估计、两阶段最小二乘法、非线性回归等多个统计过程,而且每个过程中又允许用户选择不同的方法及参数。SPSS也有专门的绘图系统,可以根据数据绘制各种图形。
MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室)。是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
Microsoft Excel是微软公司的办公软件Microsoft office的组件之一,是由Microsoft为Windows和Apple Macintosh操作系统的电脑而编写和运行的一款试算表软件。Excel 是微软办公套装软件的一个重要的组成部分,它可以进行各种数据的处理、统计分析和辅助决策操作,广泛地应用于管理、统计财经、金融等众多领域。 参考技术A 相关性分析matlab还是比较强大的,前提是能熟练运用其中的相关函数并会在matlab下编写程序本回答被提问者采纳 参考技术B 相比较来说,spss最好!详细分析如下:
1、从功能角度来说,三者基本上差不多,但matlab和spss要强于excel,前两者功能都很强大(这里说的功能仅是对相关性分析而言),而excel也可以进行相关性分析,但返回的结果和报告中涉及到的参数没有前两者多。
2、从易用性上来说,excel>spss>matlab。
3、spss给出的多种的统计检验量,使得你所说的相关性分析比较可靠,而excel给出的检验量不多,而matlab则需要记住很多命令及相关格式。
综上,spss最适合!
备战数学建模16-相关性分析SPSS&MATLAB
目录
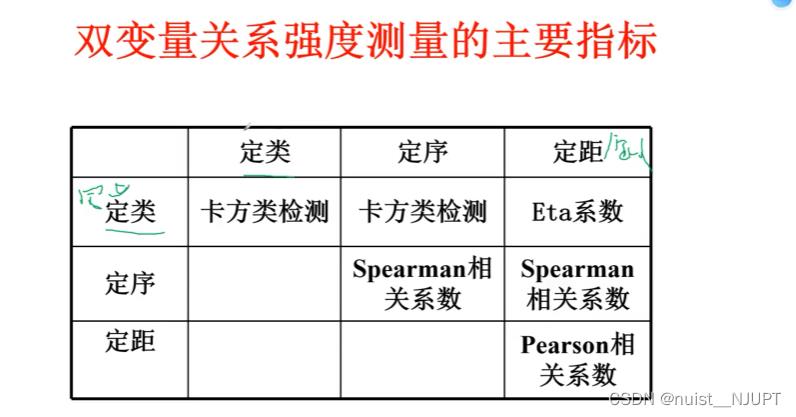
一、变量类型与相关性分析
1-变量类型及分析
2-两变量的相关性分析
Peaeson系数法需要通过t检验,通过则说明结果不具有偶然性。
pearson系数法需要是定距或者定比变量。
二、相关性检验实例
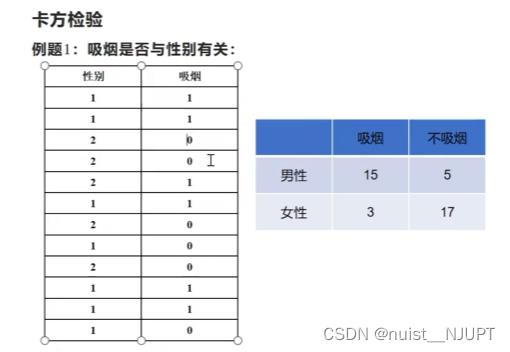
1-卡方检验
对于定类和定类的变量,我们采用卡方检验,具体如下所示:
我们使用SPSS进行相关性分析,具体步骤如下:
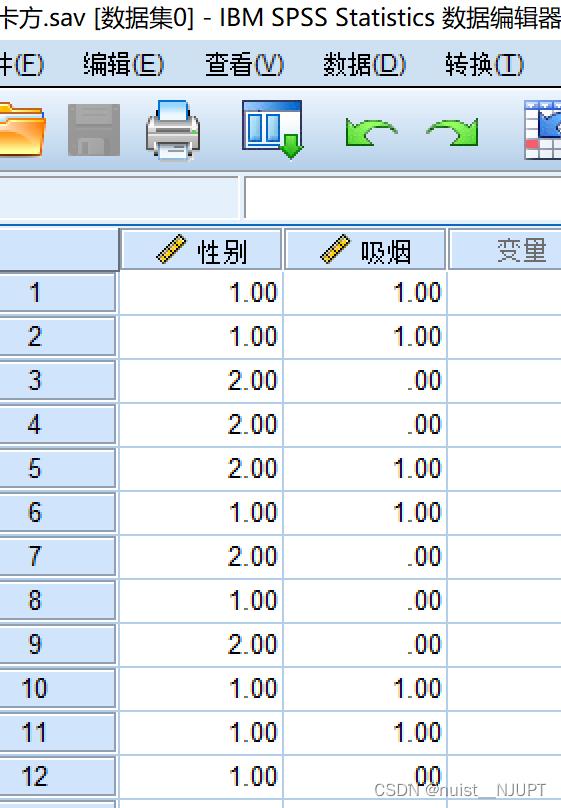
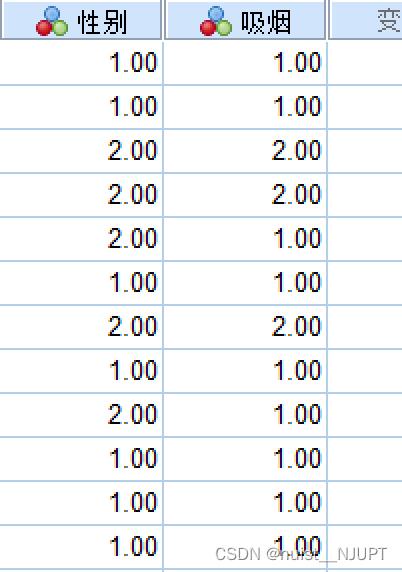
首先导入数据,如下所示:
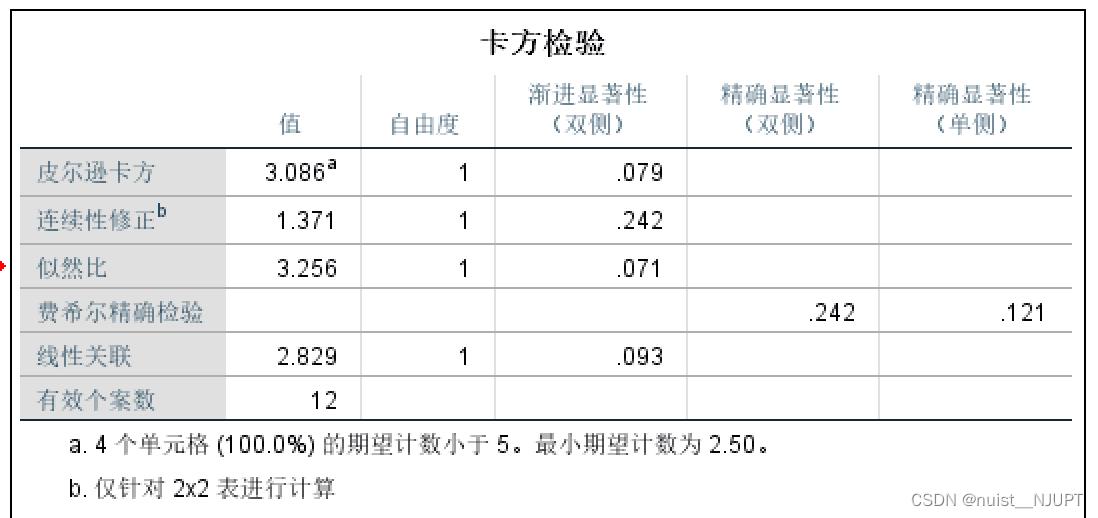
点击分析->描述统计->交叉表->统计->勾选卡方检验,检验结果可以发现,显著性0.079,大于0.05,我们认为性别和吸烟存在偶然性,不存在很强的相关性。
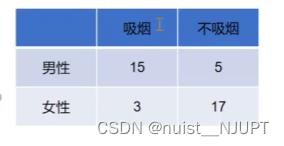
我们修改一下数据,尽量让数据一致,也就是尽量让性别和吸烟有关,数据如下:
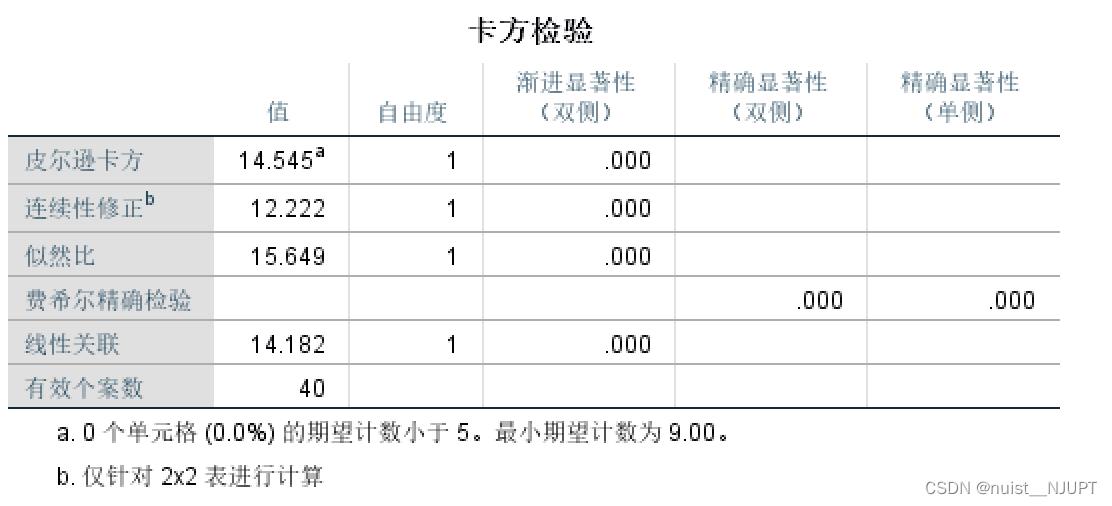
卡方检验结构如下,很明显,显著性小于0.05,说明抽烟和性别具有很强的相关性。
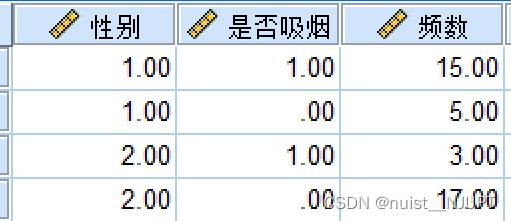
如果题目给出的数据类型是带频数的数据,如下所示,我们看一下:
在spss中点击数据->个案加权->勾选个案加权系数后。
此时再通过分析去作卡方检验就可以了。由下图可知显著性检验的值为0.00,则说明吸烟和性别由明显的相关关系。
2-Eta检验
Eta检验除了不适用于作定距和定距变量的相关性检验,其它的基本都适用。
一般是:行作为自变量,列作为因变量。我们将数据导入SPSS,然后点击分析->描述统计->交叉表->导入变量-> 在统计中勾选相关性即可。
从检验结果中发现,检验值为0.91,大于0.5,说明显著相关。
3-Pearson检验
Pearson检验可以用于定距和定比变量的相关性检验。
在SPSS中导入数据,依次点击分析->相关->双变量->勾选皮尔逊,点击确定即可。
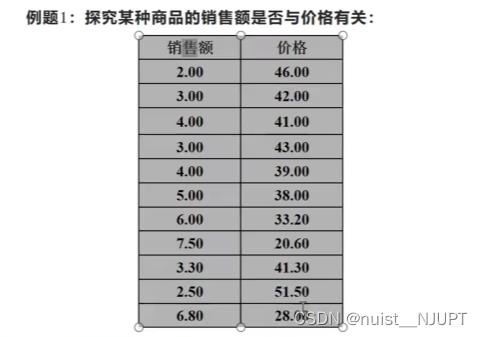
得到的检验结果如下所示,相关性的绝对值为0.95,说明销售额和价格极高相关,即相关性显著。
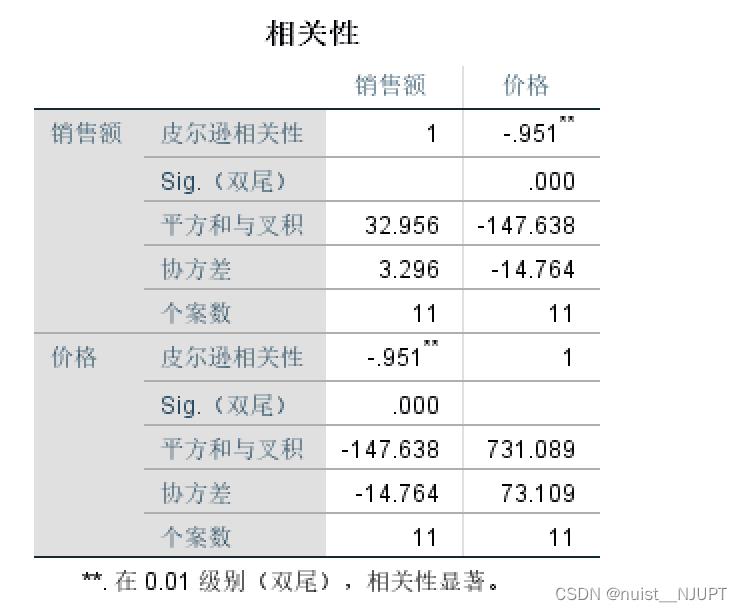
上述Pearson相关性检验可以使用如下MATLAB函数,具体如下:
function coeff = myPearson(X , Y)
% 本函数实现了皮尔逊相关系数的计算操作
% 皮尔逊相关系数计算公式(P18)及无偏相关系数矫正公式(P19)参见《现代气候统计诊断与预测技术》-魏凤英
%
% 输入:
% X:输入的数值序列
% Y:输入的数值序列
%
% 输出:
% coeff:两个输入数值序列X,Y的相关系数
%
if length(X) ~= length(Y)
error('两个数值数列的维数不相等');
return;
end
fenzi = sum((X-sum(X)/length(X)).*(Y-sum(Y)/length(Y)));
fenmu = sqrt(sum((X-sum(X)/length(X)).^2))*sqrt(sum((Y-sum(Y)/length(Y)).^2));
coef = fenzi / fenmu;
if length(X)>30
coeff = coef;
elseif length(X)>4 && length(X)<30
coeff = coef*(1+(1-coef^2)/(2*(length(X)-4))); %计算无偏相关系数加以矫正
else
coeff = coef;
fprintf('数据长度小于5 %8.4f\\n',coeff);
end
end %函数myPearson结束在命令行输入如下代码:
X = [2.00 46.00
3.00 42.00
4.00 41.00
3.00 43.00
4.00 39.00
5.00 38.00
6.00 33.20
7.50 20.60
3.30 41.30
2.50 51.50
6.80 28.00] ;
x = X(:,1) ;
y = X(:,2) ;
myPearson(x,y) 得到的检验结果如下,和SPSS检验结果一致。
也可以使用MATLAB编程实现t检验,t检验函数具体如下:
function ttest = myttest005(X , Y)
if Y <= 2
error('计算相关系数的样本量不够');
return;
end
if X == NaN
ttest = Z;
return;
end
r2 = myPearson(X , Y);%计算pearson系数
[m,n]=size(Y);
Z = m-2;%求出自由度
tvalue=abs(r2/(sqrt((1-r2^2)/Z)));
if Z == 1
tnorm = 12.71;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 2
tnorm = 4.30;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 3
tnorm = 3.18;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 4
tnorm = 2.78;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 5
tnorm = 2.57;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 6
tnorm = 2.45;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 7
tnorm = 2.37;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 8
tnorm = 2.31;
if tvalue > tnorm
ttest = X;
else
ttest = NaN;
end
elseif Z == 9
tnorm = 2.26;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 10
tnorm = 2.23;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 11
tnorm = 2.20;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 12
tnorm = 2.18;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 13
tnorm = 2.16;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 14
tnorm = 2.15;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 15
tnorm = 2.13;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 16
tnorm = 2.12;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 17
tnorm = 2.11;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 18
tnorm = 2.10;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 19
tnorm = 2.09;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 20
tnorm = 2.09;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 21
tnorm = 2.08;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 22
tnorm = 2.07;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 23
tnorm = 2.07;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 24
tnorm = 2.06;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 25
tnorm = 2.06;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 26
tnorm = 2.06;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 27
tnorm = 2.05;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 28
tnorm = 2.05;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 29
tnorm = 2.04;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
elseif Z == 30
tnorm = 2.04;
if tvalue > tnorm
ttest = Z;
else
ttest = NaN;
end
else
tnorm = 1.96;
if tvalue > tnorm
ttest = X;
else
ttest = NaN;
end
end
if ttest ~=NaN
disp('通过t检验!!!') ;
else
disp('未通过t检验!!!') ;
end %函数myttest005结束
在命令窗口调用t检验函数,具体如下:
myttest005(x,y) ;输出结果:
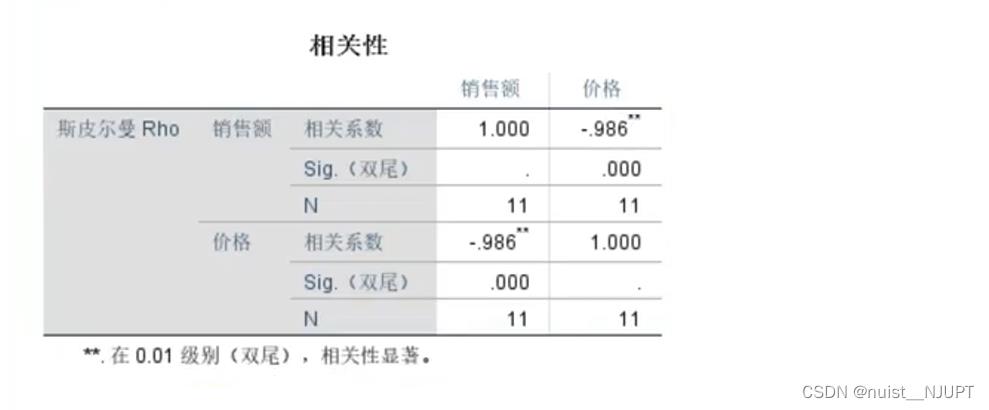
4-Speraman与kendall检验
使用SPSS,分析->相关->勾选斯皮尔曼,确定即可。可以看出结果-0.986,有极高相关性。
当然也可以使用MATLAB编程,进行斯皮尔曼检验,函数如下:
function coeff = mySpearman(X , Y)
% 本函数用于实现斯皮尔曼等级相关系数的计算操作
%
% 输入:
% X:输入的数值序列
% Y:输入的数值序列
%
% 输出:
% coeff:两个输入数值序列X,Y的相关系数
if length(X) ~= length(Y)
error('两个数值数列的维数不相等');
return;
end
N = length(X); %得到序列的长度
Xrank = zeros(1 , N); %存储X中各元素的排行
Yrank = zeros(1 , N); %存储Y中各元素的排行
%计算Xrank中的各个值
for i = 1 : N
cont1 = 1; %记录大于特定元素的元素个数
cont2 = -1; %记录与特定元素相同的元素个数
for j = 1 : N
if X(i) < X(j)
cont1 = cont1 + 1;
elseif X(i) == X(j)
cont2 = cont2 + 1;
end
end
Xrank(i) = cont1 + mean([0 : cont2]);
end
%计算Yrank中的各个值
for i = 1 : N
cont1 = 1; %记录大于特定元素的元素个数
cont2 = -1; %记录与特定元素相同的元素个数
for j = 1 : N
if Y(i) < Y(j)
cont1 = cont1 + 1;
elseif Y(i) == Y(j)
cont2 = cont2 + 1;
end
end
Yrank(i) = cont1 + mean([0 : cont2]);
end
%利用差分等级(或排行)序列计算斯皮尔曼等级相关系数
fenzi = 6 * sum((Xrank - Yrank).^2);
fenmu = N * (N^2 - 1);
coeff = 1 - fenzi / fenmu;
end %函数mySpearman结束在命令窗口输入数据,进行斯皮尔曼检验,具体如下:
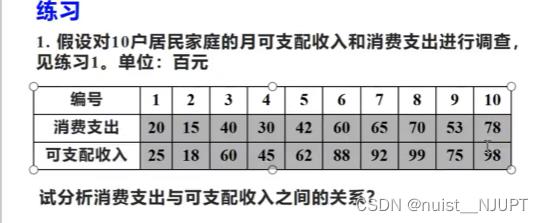
x = [20 15 40 30 42 60 65 70 53 78; 25 18 60 45 62 88 92 99 75 98];
x = x';
mySpearman(x(:,1),x(:,2))
myttest005(x(:,1),x(:,2));得到的结果:0.9879,通过t检验!!
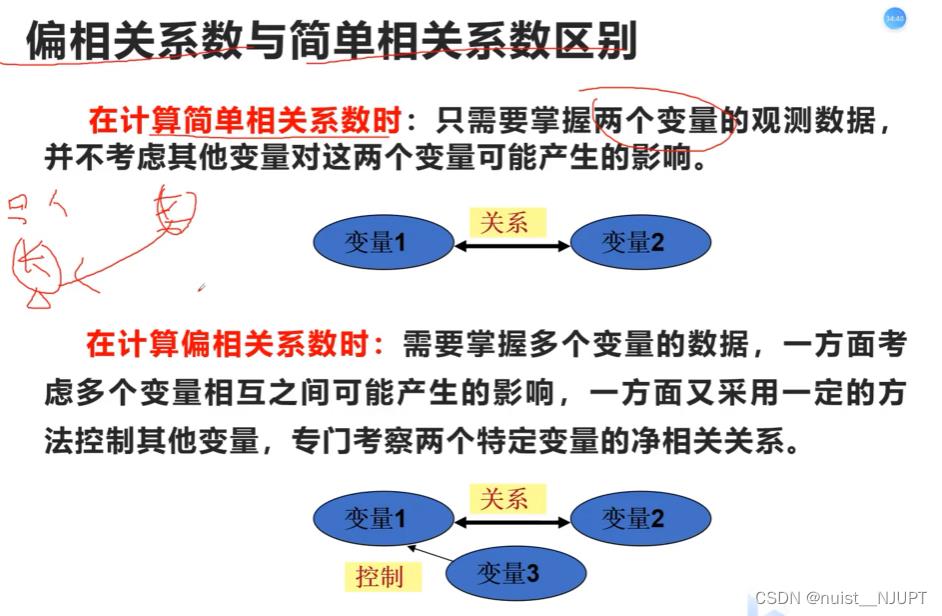
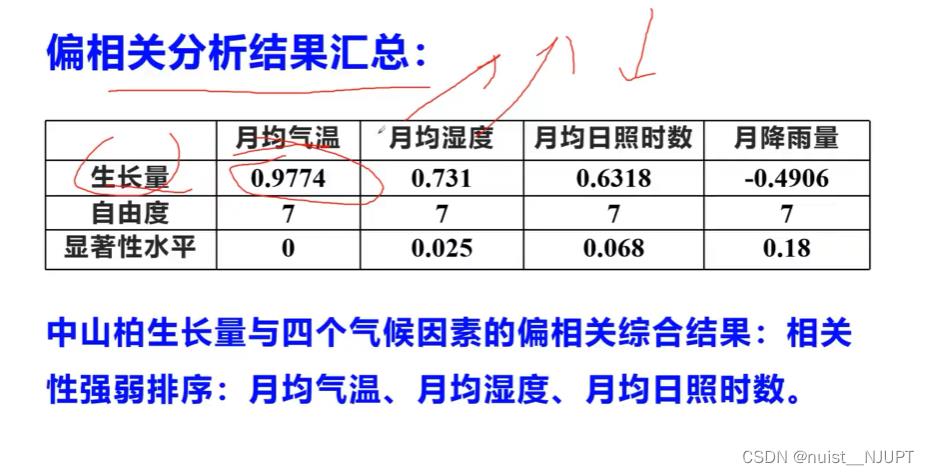
三、偏相关分析
1-偏相关分析基本概念
2-偏相关分析的案例
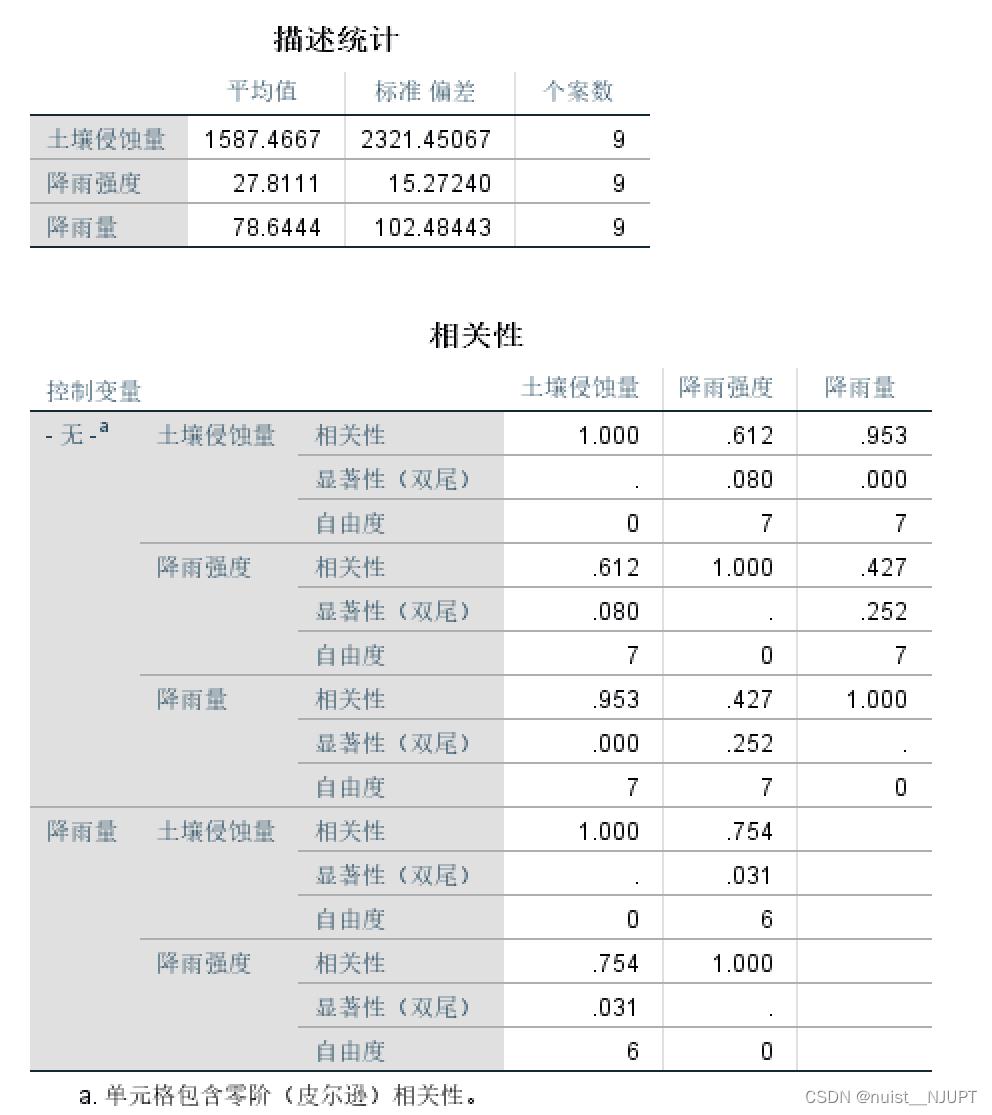
在spss中导入数据,点击分析->相关->偏相关,将评价的变量和控制的变量导入,点击去确定即可。
检验结果如下所示,从相关性表中可以发现,控制降雨量的情况下,降雨强度和土壤侵蚀量的相关性系数是0.754,如果不控制,则是0.612,说明降雨量的存在,降低了降雨强度和土壤侵蚀量的相关性。
当有变革变量的时候,两个变量分析相关性,需要控制其余变量,才能保证相关性检验更准确。
以上是关于相关性分析matlab spss excel 哪个最好的主要内容,如果未能解决你的问题,请参考以下文章