常见的排序算法( 归并排序,计数排序 , 基数排序)

Posted 2020-07-13

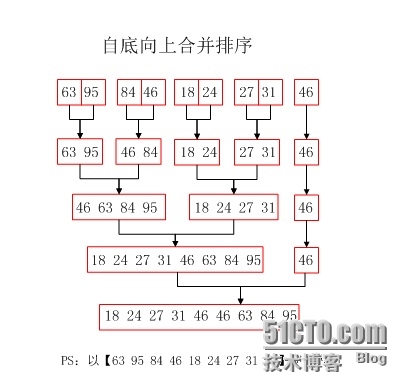
   归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

  （如果读者不太了解什么叫分治法，可以去看看《算法导论》第一二章。）

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

代码如下：

void Merge(int* a,int left, int mid, int right, int* tem)
{
	assert(a);
	assert(tem);
	int i = 0;
	int indix = mid+1;
	int begin = left;
	while(begin <= mid && indix <= right)
	{
		if(a[begin] > a[indix])
			tem[i++] = a[indix++];
		else
			tem[i++] = a[begin++];
	}
	while(begin <= mid) 
	tem[i++] = a[begin++];

	while( indix <= right)
		tem[i++] = a[indix++];

	for(int j = 0; j < i; j++)   将排好序的数组重新赋值给a
	{
		a[j+left] = tem[j];
	}
}

void mergsort(int* a,int left, int right,int*  tem)
{
	assert(a);
	assert(tem);
	int mid;
	if(left < right)
	{
		mid = (left + right)/2;
		mergsort(a,left,mid,tem);
		mergsort(a,mid+1,right,tem);
		Merge(a,left,mid,right,tem);
	}
}

bool MergeSort(int* a, int n)  
{  
	assert(a);
    int *p = new int[n];   开辟一个跟a一样大的空间，用来存放排序好的数据。
    if (p == NULL)  
        return false;  
    mergsort(a, 0, n - 1, p);  
    delete[] p;  
    return true;  
}

以上是递归算法

既然有递归算法，那也就有非递归的算法

void merge_sort(int * a, int length)
{
	assert(a);
        int i, left_min, left_max, right_min, right_max, next;  
        int *tmp = (int*)malloc(sizeof(int) * length); 

        if (tmp == NULL)
		{  
                printf("Error: out of memory\n");  
        }  

        for (i = 1; i < length; i *= 2)  
                for (left_min = 0; left_min < length - i; left_min = right_max)
				{   
                        right_min = left_max = left_min + i;  
                        right_max = left_max + i;  
                        if (right_max > length)  
                                right_max = length;  
                        next = 0;  

                        while (left_min < left_max && right_min < right_max)  
                                tmp[next++] = a[left_min] > a[right_min] ? 
								a[right_min++] : a[left_min++];  

                        while (left_min < left_max)  
                                a[--right_min] = a[--left_max]; 

                        while (next > 0)  
                                a[--right_min] = tmp[--next];  
                }  
        free(tmp);  
}

由此便可以看出递归和非递归在思想上是一致的，只是实现的方法不同罢了。

时间复杂度为O(nlogn) 这是该算法中最好、最坏和平均的时间性能。

空间复杂度为 O(n)

比较操作的次数介于(nlogn) / 2和nlogn - n + 1。

赋值操作的次数是(2nlogn)。归并算法的空间复杂度为：0 (n)

归并排序比较占用内存，但却是一种效率高且稳定的算法。

计数排序

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

算法思想编辑

计数排序对输入的数据有附加的限制条件：

1、输入的线性表的元素属于有限偏序集S；

2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。

在这两个条件下，计数排序的复杂性为O(n)。

计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

算法过程编辑

假设输入的线性表L的长度为n，L=L1,L2,..,Ln；线性表的元素属于有限偏序集S，|S|=k且k=O(n)，S={S1,S2,..Sk}；则计数排序可以描述如下：

1、扫描整个集合S，对每一个Si∈S，找到在线性表L中小于等于Si的元素的个数T(Si)；

2、扫描整个线性表L，对L中的每一个元素Li，将Li放在输出线性表的第T(Li)个位置上，并将T(Li)减1。

void CountSort(int* a,int size)
{
	int max = a[0];
	int min = a[0];
	for(int i = 1; i<size; i++)
	{
		if(a[i] > max)
			max = a[i];

		if(a[i] < min)
			min = a[i];
	}

	int* tem = new int[max-min +1]();
	
	for(int i =0; i < size; i++)
		tem[a[i] - min]++;

	int indix = 0;
	for(int i = 0; i< (max-min +1); i++)
	{
		
		while(tem[i] > 0)
		{
			a[indix++]= i + min;
			--tem[i];
		}
	}

	delete[] tem;
}

基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

其实他的实现，就想稀疏实现稀疏矩阵一样，读者可以在此借鉴，并且与之比较。

int Maxbit(int* a, int size)  //计算数组中最大值得位数。
{
	int bit = 1;
	int num = 10;
	for(int i =0; i<size;i++)
	{
		if(a[i] > num)
		{
			++bit;
			num *= 10;
		}
	}
	return bit;
}

void RadixSort(int* a, int size)
{
	int indix = Maxbit(a,size);
	int* tem = new int[size];    //记录该值
	int* count = new int[size];  //记录次数
	int radix = 1;            进位所用的值
	for(int i = 0; i<indix;i++)
	{
		for(int j = 0;j < size; j++)
		{
			count[j] = 0;
		}

		for(int j = 0; j<size; j++)
		{
			int k = (a[j]/radix) % 10;
			count[k]++;
		}
		for(int j = 1; j<size; j++)
			count[j] = count[j-1] +count [j];
		for(int j= size-1;j>=0;j--)
		{
			int k = (a[j]/radix) % 10;
			tem[count[k] -1] = a[j];
			count[k]--;
		}

		for(int j = 0;j < size; j++)
		{
			a[j] = tem[j];
		}

		radix = radix * 10;
		
	}

	delete[] tem;
	delete[] count;
}

 以上形象图解可看上篇博文中的超链接，给予读者形象的理解和解答

  这篇博文列举了归并排序,计数排序 , 基数排序，基本可以掌握其中概要，管中窥豹，不求甚解。如果你有任何建议或者批评和补充，请留言指出，不胜感激，更多参考请移步互联网。