梯度寻优与logistic算法

Posted 2020-11-10 韩非囚秦

一、一些基本概念

　　最优化：在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优。高中学过的线性规划就是一类典型的最优化问题。

　　凸集：在集合空间中，凸集就是一个向四周凸起的图形。用数学语句描述就是：集合边界任意两点连线上的所有点都在这个集合内部。

　　超平面：能够用于切割已给集合的点集。数学公式为$X={x|c^T=z}$。它的意义在于能够将一个凸集分为两部分。

　　举例说明。对于二维空间，用一条直线划分给定的散点，则有$y - ax - b = 0 $。它就是一个超平面，“超”在b这个维度上，在这里它是一个定值。同样地，对于三维空间，用一个平面划分，择有超平面$z - ax - by - c = 0$。

　　支撑超平面：使所有集合内的点位于同一侧的超平面。

　　凸集分离定理：如果两个凸集没有交叉或重合，则可以用超平面(支撑超平面)分割这两个凸集。该定理为线性分类提供了理论基础。

　　凸函数：凸函数是凸集中元素的数学特征，是凸集的数学公式表达。用以下公式来表示凸集：

　　$f(ax_1 + (1 - \\alpha x_2)) \\le f(\\alpha x_1 +f(1 - \\alpha) x_2)$

　　因为凸集是一个集合，没有对元素是否连续进行规定，所以凸函数没有要求是连续的或可微的。

　　局部最优和全局最优：它实际是函数的极值和最值的问题。对损失函数$\\sum (y - f(y))^2$(这里f(y)是用各种算法来计算预测值)来说，我们只想要最小值而不是极值。损失函数的定义借鉴了统计学中样本的二阶中心距的理论和方法。它是连续可导的，因此可以求最值。

二、Logistic回归

　　1、logistic回归

　　logistic回归是线性回归的一种扩展，它将线性回归的结果按照sigmoid函数进行分类。在计量模型中，logistic回归是一种无序分类算法，即要求分类变量不是等级有序的。与logistic相反，probit回归则要求分类变量必须是等级有序的。我们仍然可以用线性回归的模型评价方法来检验和优化logistic回归。

　　logistic是一种线性分类器，无法解决异或问题，因此要求样本尽量是线性可分的。它旨在散点中找到最佳的一条回归线，把所有的散点分到回归线两侧，这条回归线由sigmod函数确定，并由梯度下降算法去迭代实现。

　　从神经网络角度看，logistic回归算是一种单层单节点(单神经元)感知器，sigmoid函数是激活函数，梯度下降算法是一种优化策略。

　　2、sigmoid函数

　　sigmoid函数，或称单极性阈值函数的公式为:

　　　　$$f(x) = \\frac{1}{1 + e^{-x}}，其导数为f\'(x) = f(x)(1 - f(x))$$

　　它有两个作用：一是将线性回归的预测值归一化；二是放大器，即远离回归线的sigmoid值会接近0或1，靠近回归线的值在0.5附近。

　　3、梯度下降算法

　　梯度下降算法是一种优化策略。梯度即偏导数，物理意义是因变量取某值时，某个(或所有)自变量(特征)在此刻的分量。

　　梯度下降算法需要注意三个点：

　　首先，需要事先声明损失函数。因为损失函数通常是凸函数，并且一定存在最小值。所以所有偏导数同时为0的点一定是极值点。实际上这个条件很难达到，所以通常采用逐步逼近(迭代)法来求极值。

　　其次，梯度下降算法在每一次迭代时取梯度的负值，直至使损失函数最小。

　　举例说明。

　　假如规定更新公式$x =  x - \\eta * \\frac{\\triangle y}{\\triangle x}$。其中，$\\eta$表示学习率(或称步长)，$\\frac{\\triangle f}{\\triangle x}$表示x分量的偏导数，f表示多元函数符合函数。那么在梯度下降的每一次迭代中，都会按照公式更新x本身。

　　如下图所示。在C点时，偏导数值为负，由更新公式，$x = x_c + |\\frac{\\triangle f}{\\triangle x_c|$，知道x将不断增大(往右移动)，并最终到达B点。同理，在A点时，偏导数值为正，由更新公式，$x = x_c - |\\frac{\\triangle f}{\\triangle x_c|$，知道x将不断减小(往左移动)，并最终到达B点。

　　　　　　　　　　　　　　　　　　　　

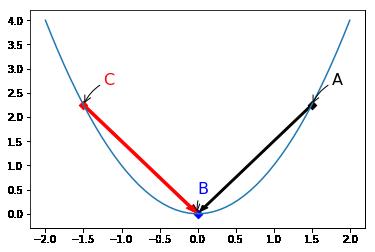
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-2, 2)
y = np.power(x,2)

plt.plot(x, y)
plt.annotate(
    s="A", xy=(1.5, np.power(1.5, 2)), xycoords="data", color="black",
    xytext=(20, 20), textcoords="offset points", fontsize=16,
    arrowprops=dict(arrowstyle="->", connectionstyle="arc3, rad=0.2")
)
plt.annotate(
    s="C", xy=(-1.5, np.power(-1.5, 2)), xycoords="data", color="red",
    xytext=(20, 20), textcoords="offset points", fontsize=16,
    arrowprops=dict(arrowstyle="->", connectionstyle="arc3, rad=0.2")
    
)
plt.annotate(
    s="B", xy=(0, 0), xycoords="data",  color="blue",
    xytext=(0, 20), textcoords="offset points", fontsize=16,
    arrowprops=dict(arrowstyle="->", connectionstyle="arc3, rad=0.2"),
    
)
plt.scatter(1.5, np.power(1.5, 2), marker="D", c="black")
plt.scatter(-1.5, np.power(-1.5, 2), marker="D", c="red")
plt.scatter(0, 0, marker="D", c="blue")
plt.arrow(-1.5, np.power(-1.5, 2), 1.4, -2.1, width=0.04, color="red")
plt.arrow(1.5, np.power(1.5, 2), -1.4, -2.1, width=0.03, color="black")
plt.show()

图形代码

　　学习率$\\eta$控制每次移动的幅度(步长)，如果步长过大，会导致移动过程中会“跳过”B点，并出现来回震荡现象。因此，在众多随机梯度下降算法之外，也会有各种控制步长的优化方法。比如增加动量项等。

　　对于下图这种多个维度的，按照单个维度进行逐一分析即可。

　　　　　　　　　　　　　　　　

　　对每个分量进行独立求偏导并进行迭代，意味着这些分量要相互独立(或要满足最大似然估计)。因此要注意分量(特征列向量)之间的线性相关程度以及共线性问题。

　　第三，梯度下降算法需要设置激活函数。激活函数解决了线性分类器无法克服的异或问题，使得多个(线性分类器+激活函数)能够圈出多边形，来更细致的对散点进行分类。常见的激活函数有单位阶跃函数、单极性阈值函数、双极性阈值函数等。

　　第四，梯度下降算法需要使用BP误差调整策略。常见的误差调整策略有：

　　　　　　　　　　　　

　　

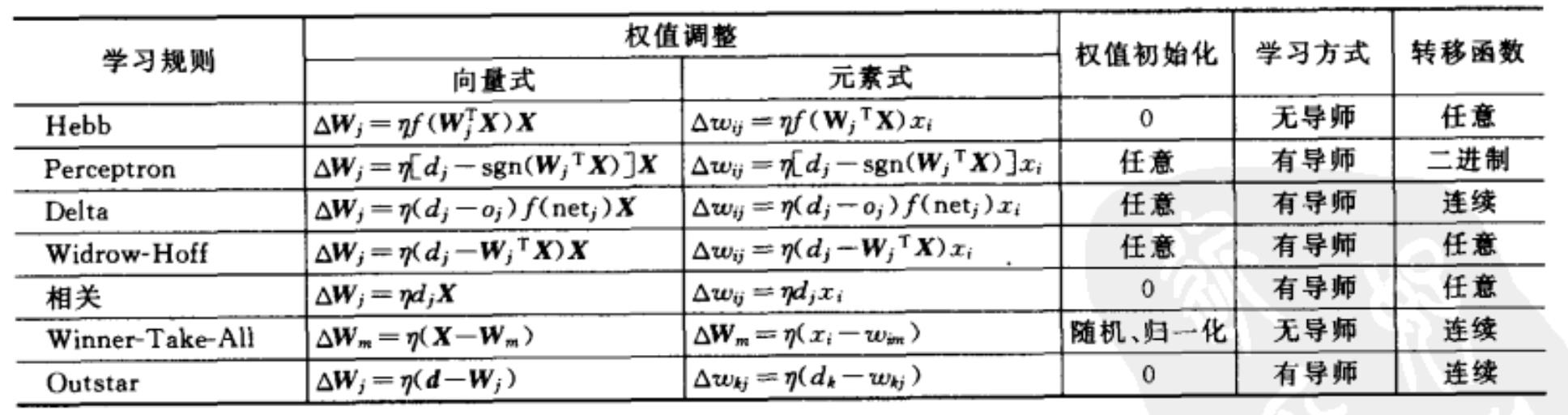
　　4、算法流程

　　　　初始化每个回归系数(包括常数项)，即初始化权重矩阵。

　　　　重复计算：

　　　　　　计算整个数据集的梯度

　　　　　　使用梯度下降算法更新回归系数

　　　　返回回归系数

三、python3实现logistic回归算法

　　1、python3实现logistic回归算法

　　LoadDataSet载入数据集。Plot绘制图形。数据集https://files.cnblogs.com/files/kuaizifeng/testSet.txt.zip。

　　LgcRegr实现logistic算法。

　　　　sigmoid激活函数。也可以改成双极性阈值函数，但相应的算法需要调整。

　　　　fit函数：训练数据集。

　　　　pred函数：预测分类。

　　　　error函数：误差计算。

　　　　gd函数[可选]：批量梯度下降，这里没设定batch。

　　　　rgd函数[可选]：随机梯度下降。

　　　　srgd函数[可选]：增加动量项的随机梯度下降。

　　　　drgd函数[可选]：使用delta学习规则作为误差调整策略。需要对神经网络的学习规则有一定的了解。

　　

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

class LoadDataSet(object):
    def get_dataSet(self):
        dataSet = pd.read_csv(
            "machinelearninginaction-master/Ch05/testSet.txt", 
            sep="\\t", header=None,
            names=["x1", "x2", "y"],
        )
        data = np.array(dataSet[["x1", "x2"]]).tolist()
        labels = list(dataSet["y"])
        self.dataSet = dataSet
        return data, labels
    
class Plot(object):
    def plot(self, dataSet, weights):
        """绘图"""
        plt.figure()
        Arr0 = dataSet[dataSet["y"] == 0]
        Arr1 = dataSet[dataSet["y"] == 1]
        plt.scatter(Arr0["x1"], Arr0["x2"], c="blue")
        plt.scatter(Arr1["x1"], Arr1["x2"], c="red")
        x1_test = np.linspace(-4, 4)
        # np.double：从多维单元素的数组中取出单元素值
        x2_test = -(np.double(weights[0]) + np.double(weights[1]) * x1_test) / np.double(weights[2])
        # 超平面 weights[0] + weight[1]*x1 + weights[2]*x2 = 0，因此得到x2_test
        plt.plot(x1_test, np.double(x2_test), c="c")
        plt.show()
        
class LgcRegr(LoadDataSet, Plot):
    """梯度下降gradient descent """
    def __init__(self):
        super().__init__()
    
    def sigmoid(self, inX):
        """单极性阈值函数及其导数"""
        return 1.0/(1 + np.exp(-inX))
        
    def fit(self, dataSet, labels, **kwargs):
        """训练模型"""
        dataMat = np.mat(dataSet)
        dataMat = np.c_[np.ones(dataMat.shape[0]), dataMat]  # 把dataSet改成矩阵，并增加一列
        labelMat = np.mat(labels).T # 标签列
        learning_rate = kwargs.get("learning_rate", 0.001)
        steps = kwargs.get("steps", 500)
        self.weights = getattr(self, kwargs.get("mode", "gd"))(dataMat, labelMat, learning_rate, steps)
        return self.weights
    def error(self, dataSet, labels):
        """计算误差"""
        dataMat = np.mat(dataSet)
        dataMat = np.c_[np.ones((dataMat.shape[0], 1)),dataMat]
        error = np.dot(dataMat, self.weights) - np.mat(labels).T
        return np.double(np.round(sum(np.power(error, 2)), 4))
    
    def pred(self, testSet):
        testSet = np.array(testSet)
        if not testSet.shape[1] >= 2:  # 单个样本要进行处理
            testSet = np.mat([testSet])
        testSet = np.C_[np.ones((testSet.shape[0], 1)), testSet]  # 增加一列常数项
        predmat = self.sigmoid(np.dot(testSet, self.weights))  # 预测值矩阵
        self.pred = []
        for i in range(testSet.shape[0]):
            self.pred.append(np.round(np.double(out[i, 0])))
        return self.pred
    
    def gd(self, dataMat, labelMat, learning_rate, steps):
        """普通随机下降gradient_descent"""
        weights = np.ones((dataMat.shape[1], 1))
        for i in range(steps):
            net = np.dot(dataMat, weights)
            weights = weights + learning_rate * dataMat.T * (labelMat - self.sigmoid(net)) # 一次需要计算整个矩阵
        # 参见Perceptro学习规则，这里把sgn函数换成了sigmoid函数
        return weights
    def rgd(self, dataMat, labelMat, learning_rate, steps):
        """随机梯度下降random_gradient_descent"""
        weights = np.ones((dataMat.shape[1], 1))
        for i in range(steps):
            for j, row in enumerate(dataMat):
                net = sum(np.dot(row, weights))
                weights = weights + learning_rate * row.T * (labelMat[j] - self.sigmoid(net)) # 只计算一行数据
        return weights
    
    def srgd(self, dataMat, labelMat, learning_rate, steps):
        """随机梯度西下降，增加动量项"""
        weights = np.ones((dataMat.shape[1], 1))
        for i in range(steps):
            for j, _ in enumerate(dataMat):
                rate = 4 / (1.0 + j + i) + learning_rate  # 更新学习率
                index = np.random.randint(0, dataMat.shape[0])  # 随机选择数据行
                row = dataMat[index]
                net = sum(np.dot(row, weights))
                weights = weights + rate * row.T * (labelMat[index] - self.sigmoid(net))
        return weights  # weights.A可以将矩阵转化为数组
    
    def drgd(self, dataMat, labelMat, learning_rate, steps):
        """用delta学习规则训练"""
        weights = np.ones((dataMat.shape[1], 1))
        for i in range(steps):
            for j, row in enumerate(dataMat):
                rate = 4 / (1.0 + j + i) + learning_rate  # 更新学习率
                # 这里设损失函数为 E = 1/2 * (d - f(X.T * W))^2
                net = np.double(np.dot(row, weights))  # 计算W.T * X
                error = np.double(labelMat[j]) - self.sigmoid(net)  # 计算(d - o)
                fd =  self.sigmoid(net).T * (1 - self.sigmoid(net)) # 计算 f\'(x)，这里f是sigmoid
                delta = -np.double(error * fd ) * row.T   # 计算delta E = (d - o) * f\'(x) * X.T
                weights = weights - rate * delta  # 更新权重 -rate * delta
        return weights

　　运行以下代码：

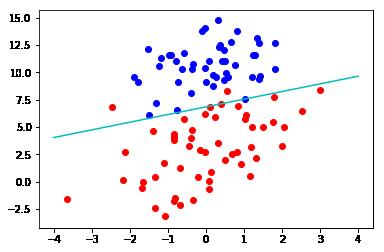
logis = LgcRegr()
data = logis.get_dataSet()
weights = logis.fit(*data, mode="drgd", steps=100)  # mode可以选rgd、gd、srgd
# print(weights)
logis.plot(logis.dataSet, weights)
# logis.error(*data)

　　结果为：

　　　　　　　　　　　　　　　　　　　　　　　　

　　2、sikit-learn实现logistic回归算法

　　官网http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

from sklearn.linear_model import LogisticRegression
import pickle

logistic = LogisticRegression()
logistic.fit(*data)
# logistic.sparsify()   # 查看模型的参数设置 和logistic.densify()一样
logistic.get_params()   # 查看模型的参数设置
logistic.predict_proba(data[0])  # 每个样本对标签的每个类别的所属概率值
# 持久化模型，以后拿来预测即可
pickle.dump(logistic, open("logistic.txt", "wb"))  # 保存模型
lgc = pickle.load(open("logistic.txt", "rb"))   # 载入模型
logistic.predict(data[0])  # 预测，这里用了原始数据集
logistic.score(*data)   # 准确率