Logistic回归之基于最优化方法的最佳回归系数确定

Posted 2020-10-07 我在看代码

 

之前学习Java的时候，用过一个IDE叫做EditPlus,虽然他敲代码的高亮等体验度不及eclipse，但是打开软件特别快捷，现在也用他读python特别方便。

 

训练算法:：使用梯度上升找到最佳参数

之前看过吴恩达的视频的同学们，听得比较多的就是梯度下降算法，但是梯度上升算法和梯度下降算法本质是是一样的，只是梯度计算的时候加减号不一样罢了。

 

 1 def loadDataSet():
 2     dataMat = []; labelMat = []
 3     fr = open(\'testSet.txt\')
 4     for line in fr.readlines():
 5         lineArr = line.strip().split()
 6         dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
 7         labelMat.append(int(lineArr[2]))
 8     return dataMat,labelMat
 9 
10 def sigmoid(inX):
11     return 1.0/(1+exp(-inX))
12 
13 def gradAscent(dataMatIn, classLabels):
14     dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
15     labelMat = mat(classLabels).transpose() #convert to NumPy matrix
16     m,n = shape(dataMatrix)
17     alpha = 0.001
18     maxCycles = 500
19     weights = ones((n,1))
20     for k in range(maxCycles):              #heavy on matrix operations
21         h = sigmoid(dataMatrix*weights)     #matrix mult
22         error = (labelMat - h)              #vector subtraction
23         weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
24     return weights

第一个函数打开testSet。txt并逐行读取，每行前两个值分别是x1和x2，第三个值是对应的类别标签。为了方便计算，该函数还将x0的值设为1.0

第二个函数是sigmoid函数，x为0时，函数值为0.5，x增大时，函数值将不断增大逼近1。

第三个函数有两个参数，第一个是2维数组，每列代表不同的特征，每行代表每个训练样本。我们采用100个样本的简单数据集它包含两个特征x1,x2，再加上第0维特征x0,所以dataMatln里面存放的是100*3的矩阵。

 

 

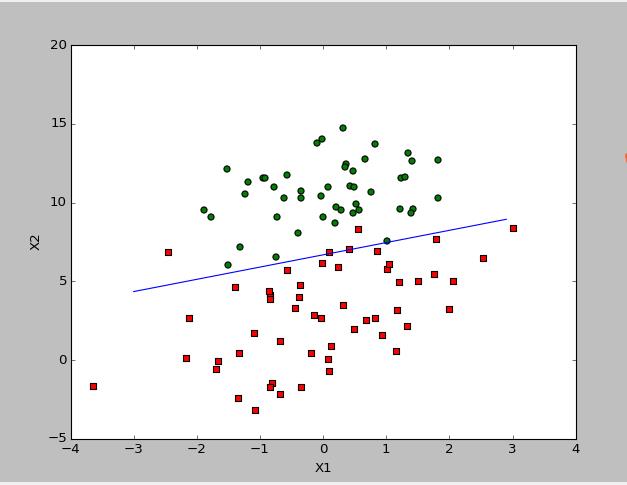
分析数据：画出决策边界

 1 def plotBestFit(weights):
 2     import matplotlib.pyplot as plt
 3     dataMat,labelMat=loadDataSet()
 4     dataArr = array(dataMat)
 5     n = shape(dataArr)[0] 
 6     xcord1 = []; ycord1 = []
 7     xcord2 = []; ycord2 = []
 8     for i in range(n):
 9         if int(labelMat[i])== 1:
10             xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
11         else:
12             xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
13     fig = plt.figure()
14     ax = fig.add_subplot(111)
15     ax.scatter(xcord1, ycord1, s=30, c=\'red\', marker=\'s\')
16     ax.scatter(xcord2, ycord2, s=30, c=\'green\')
17     x = arange(-3.0, 3.0, 0.1)
18     y = (-weights[0]-weights[1]*x)/weights[2]
19     ax.plot(x, y)
20     plt.xlabel(\'X1\'); plt.ylabel(\'X2\');
21     plt.show()

 

>>> from numpy import *
>>> reload(logRegres)
<module \'logRegres\' from \'D:\\Python27\\logRegres.pyc\'>
>>> weights=logRegres.gradAscent(dataArr,labelMat)
>>> logRegres.plotBestFit(weights.getA())

 

训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都需要遍历整个数据集。改进的方法是一次仅使用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与在线学习相对应，一次处理所有数据被称作是批处理。

1 def stocGradAscent0(dataMatrix, classLabels):
2     m,n = shape(dataMatrix)
3     alpha = 0.01
4     weights = ones(n)   #initialize to all ones
5     for i in range(m):
6         h = sigmoid(sum(dataMatrix[i]*weights))
7         error = classLabels[i] - h
8         weights = weights + alpha * error * dataMatrix[i]
9     return weights

 

>>> from numpy import *
>>> reload(logRegres)
<module \'logRegres\' from \'D:\\Python27\\logRegres.pyc\'>
>>> dataArr,labelMat=logRegres.loadDataSet()
>>> weights=logRegres.stocGradAscent0(array(dataArr),labelMat)
>>> logRegres.plotBestFit(weights)

 

 

改进的随机梯度上升算法

 1 def stocGradAscent1(dataMatrix, classLabels, numIter=150):
 2     m,n = shape(dataMatrix)
 3     weights = ones(n)   #initialize to all ones
 4     for j in range(numIter):
 5         dataIndex = range(m)
 6         for i in range(m):
 7             alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not 
 8             randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
 9             h = sigmoid(sum(dataMatrix[randIndex]*weights))
10             error = classLabels[randIndex] - h
11             weights = weights + alpha * error * dataMatrix[randIndex]
12             del(dataIndex[randIndex])
13     return weights

 增加了亮出代码来进行改进。一方面，alpha在每次迭代的时候都会调整，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为存在一个常数项。

另一方面，通过随机选取样本来更新回归系数。

>>> dataArr,labelMat=logRegres.loadDataSet()
>>> weights=logRegres.stocGradAscent1(array(dataArr),labelMat)
>>> logRegres.plotBestFit(weights)

 

 

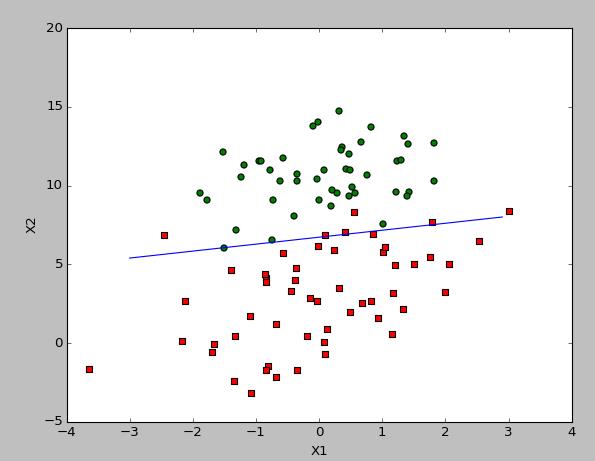
 从疝气病症预测病马的死亡率

 1 def classifyVector(inX, weights):
 2     prob = sigmoid(sum(inX*weights))
 3     if prob > 0.5: return 1.0
 4     else: return 0.0
 5 
 6 def colicTest():
 7     frTrain = open(\'horseColicTraining.txt\'); frTest = open(\'horseColicTest.txt\')
 8     trainingSet = []; trainingLabels = []
 9     for line in frTrain.readlines():
10         currLine = line.strip().split(\'\\t\')
11         lineArr =[]
12         for i in range(21):
13             lineArr.append(float(currLine[i]))
14         trainingSet.append(lineArr)
15         trainingLabels.append(float(currLine[21]))
16     trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
17     errorCount = 0; numTestVec = 0.0
18     for line in frTest.readlines():
19         numTestVec += 1.0
20         currLine = line.strip().split(\'\\t\')
21         lineArr =[]
22         for i in range(21):
23             lineArr.append(float(currLine[i]))
24         if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
25             errorCount += 1
26     errorRate = (float(errorCount)/numTestVec)
27     print "the error rate of this test is: %f" % errorRate
28     return errorRate
29 
30 def multiTest():
31     numTests = 10; errorSum=0.0
32     for k in range(numTests):
33         errorSum += colicTest()
34     print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))

第一个函数，如果sigmoid值大于0.5函数返回1，否则返回0.

第二个函数，用于打开测试集和训练集，并对数据进行格式化处理的函数。

第三个函数，调用第二个函数10次并求结果的平均值。

                   .-\' _..`.                  /  .\'_.\'.\'                 | .\' (.)`.                 ;\'   ,_   `. .--.__________.\'    ;  `.;-\'|  ./               /|  |               / `..\'`-._  _____, ..\'     / | |     | |\\ \\    / /| |     | | \\ \\   / / | |     | |  \\ \\  /_/  |_|     |_|   \\_\\ |__\\  |__\\    |__\\  |__\\