用Tensorflow完成简单的线性回归模型

Posted 2020-11-09 SelenaF

 思路：在数据上选择一条直线y=Wx+b，在这条直线上附件随机生成一些数据点如下图，让TensorFlow建立回归模型，去学习什么样的W和b能更好去拟合这些数据点。

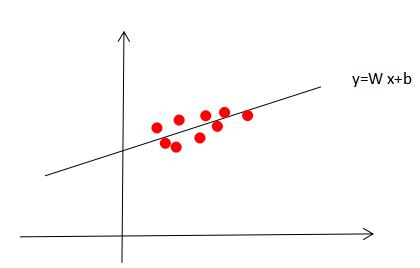
1）随机生成1000个数据点，围绕在y=0.1x+0.3 周围，设置W=0.1，b=0.3，届时看构建的模型是否能学习到w和b的值。

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
num_points=1000     
vectors_set=[]
for i in range(num_points):
    x1=np.random.normal(0.0,0.55)   #横坐标，进行随机高斯处理化，以0为均值，以0.55为标准差
    y1=x1*0.1+0.3+np.random.normal(0.0,0.03)   #纵坐标，数据点在y1=x1*0.1+0.3上小范围浮动
    vectors_set.append([x1,y1])
    x_data=[v[0] for v in vectors_set]
    y_data=[v[1] for v in vectors_set]
    plt.scatter(x_data,y_data,c=\'r\')
    plt.show()

构造数据如下图

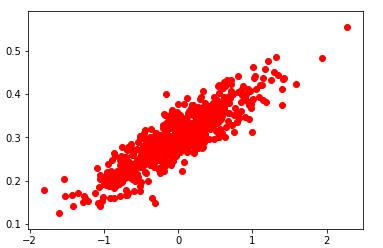
2）构造线性回归模型，学习上面数据图是符合一个怎么样的W和b

    W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name=\'W\')  # 生成1维的W矩阵，取值是[-1,1]之间的随机数
    b = tf.Variable(tf.zeros([1]), name=\'b\') # 生成1维的b矩阵，初始值是0
    y = W * x_data + b     # 经过计算得出预估值y  
    loss = tf.reduce_mean(tf.square(y - y_data), name=\'loss\') # 以预估值y和实际值y_data之间的均方误差作为损失
    optimizer = tf.train.GradientDescentOptimizer(0.5) # 采用梯度下降法来优化参数  学习率为0.5
    train = optimizer.minimize(loss, name=\'train\')  # 训练的过程就是最小化这个误差值
    sess = tf.Session()
    init = tf.global_variables_initializer()
    sess.run(init)
    print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))  # 初始化的W和b是多少
    for step in range(20):   # 执行20次训练
      sess.run(train)      
      print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) # 输出训练好的W和b

打印每一次结果，如下图，随着迭代进行，训练的W、b越来越接近0.1、0.3，说明构建的回归模型确实学习到了之间建立的数据的规则。loss一开始很大，后来慢慢变小，说明模型表达效果随着迭代越来越好。

W = [-0.9676645] b = [0.] loss = 0.45196822

W = [-0.6281831] b = [0.29385352] loss = 0.17074569

W = [-0.39535886] b = [0.29584622] loss = 0.07962803

W = [-0.23685378] b = [0.2972129] loss = 0.03739688

W = [-0.12894464] b = [0.2981433] loss = 0.017823622

W = [-0.05548081] b = [0.29877672] loss = 0.008751821

W = [-0.00546716] b = [0.29920793] loss = 0.0045472304

W = [0.02858179] b = [0.2995015] loss = 0.0025984894

W = [0.05176209] b = [0.29970136] loss = 0.0016952885

W = [0.06754307] b = [0.29983744] loss = 0.0012766734

W = [0.07828666] b = [0.29993007] loss = 0.001082654

W = [0.08560082] b = [0.29999313] loss = 0.0009927301

W = [0.09058025] b = [0.30003607] loss = 0.0009510521

W = [0.09397022] b = [0.30006528] loss = 0.00093173544

W = [0.09627808] b = [0.3000852] loss = 0.00092278246

W = [0.09784925] b = [0.30009875] loss = 0.000918633

W = [0.09891889] b = [0.30010796] loss = 0.00091670983

W = [0.0996471] b = [0.30011424] loss = 0.0009158184

W = [0.10014286] b = [0.3001185] loss = 0.00091540517

W = [0.10048037] b = [0.30012143] loss = 0.0009152137

W = [0.10071015] b = [0.3001234] loss = 0.0009151251

注：以上内容为我学习唐宇迪老师的Tensorflow课程所做的笔记