数据结构与算法-线性表之双向链表

Posted 2020-11-09 robot developer

参考博客：

http://www.cnblogs.com/skywang12345/p/3561803.html

https://blog.csdn.net/howlaa/article/details/38513235

1、概述

线性表是一种线性结构，由数组、单项链表和双向链表组成，这里讲讨论双向链表的理论知识和实现代码。

双向链表和单项链表类似，双向链表由两个指针作为指针域，分别指向前驱节点和后驱节点。可以从任何节点开始向前或者向后删除、增加、查找节点。

双链表的示意图如下：

 

在插入节点的时候有两种方式：前插法和尾插法，这里介绍的是前插法。如下图所示：

注意，一定要理解这个图，不然理解后面代码的插入操作会有问题

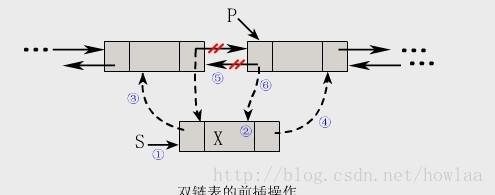
 代码描述：

1 void DInsertBefore(DListNode *p,DataType x){  
2         //带头节点的双链表中，将值为X的新节点插入P之前，设P!=null  
3         DListNode *s = malloc(sizeof(DListNode));//1、这个是申请一个新节点，用来放X的。  
4         s->data = x;//2、把新节点的数据放为x  
5         s->prior = p->prior;//3、这个是新节点的前驱节点接到原来P的前驱节点上  
6         s->next = p;//4、新节点的后节点接到P上  
7         p->prior->next = s;//5、这个是把P的前驱节点O的后继节点接到S上  
8         p->prior = s;//6、把P的前驱节点接到S上。  
9     }  

2、代码编写：

 doubleLink.h

#ifndef _DUBLE_LINK_
#define _DUBLE_LINK_

namespace DoubleLinkSpace{

    template<class T>
    class Dnode{
    public:
        T value;
        Dnode *prev;
        Dnode *next;
    public:
        Dnode(){}
        Dnode(T t, Dnode *prev, Dnode *next){
            value = t;
            this->prev = prev;
            this->next = next;
        }
    };

    template<class T>
    class DoubleLink{
    public:
        DoubleLink();
        ~DoubleLink();

        int size();
        bool is_empty();

        T get_fist();
        T get_last();
        T get(int index);

        int insert(int index, T t);
        int insert_first(T t);
        int append_last(T t);

        int del(int index);
        int del_first();
        int del_last();
    private:
        int count;
        Dnode<T> *phead;
        Dnode<T> *get_node(int index);
    };

    //构造函数
    template<class T>
    DoubleLink<T>::DoubleLink(){
        phead = new Dnode<T>();
        phead->next = phead->prev = phead;
        count = 0;
    }

    //析构函数
    template<class T>
    DoubleLink<T>::~DoubleLink(){
        Dnode<T> *ptmp;
        Dnode<T> *pnode = phead->next;
        //删除所有节点
        while (pnode != phead)
        {
            ptmp = pnode;
            pnode = pnode->next;
            delete ptmp;
        }
        delete phead;
    }

    //获取链表节点数
    template<class T>
    int DoubleLink<T>::size(){
        return count;
    }

    //判断链表是否为空
    template<class T>
    bool DoubleLink<T>::is_empty(){
        return (count == 0) ? true : false;
    }

    //二分查找实现链表节点查找
    template<class T>
    Dnode<T> *DoubleLink<T>::get_node(int index){
        if (index < 0 || index >= count)
            return nullptr;
        if (index <= count / 2){
            int i = 0;
            Dnode<T>* pindex = phead->next;
            while (i < index){
                pindex = pindex->next;
                i++;
            }
            return pindex;
        }

        int j = 0;
        int rindex = count - index - 1;
        Dnode<T>* rpindex = phead->prev;
        while (j < rindex){
            rpindex = rpindex->prev;
            j++;
        }
        return rpindex;
    }


    //获取节点的数据域
    template<class T>
    T DoubleLink<T>::get(int index){
        Dnode<T> *tmpNode = get_node(index);
        if (tmpNode != nullptr){
            return tmpNode->value;
        }
        else{
            T ret;
            return ret;
        }

    }

    //获取第一个节点值
    template<class T>
    T DoubleLink<T>::get_fist(void){
        Dnode<T> *tmpNode = get_node(0);
        if (tmpNode != nullptr){
            return tmpNode->value;
        }
        else{
            return 0;
        }

    }

    //获取最后一个节点值
    template<class T>
    T DoubleLink<T>::get_last(void){
        Dnode<T> *tmpNode = get_node(count - 1);
        if (tmpNode != nullptr){
            return tmpNode->value;
        }
        else{
            return 0;
        }
    }

    //前插法插入节点
    template<class T>
    int DoubleLink<T>::insert(int index, T t){
        if (index == 0){
            return insert_first(t);
        }
        Dnode<T> *pindex = get_node(index);
        Dnode<T> *pnode = new Dnode<T>(t, pindex->prev, pindex);//pnode->prev = pindex->prev;pnode->next = pindex
        pindex->prev->next = pnode;
        pindex->prev = pnode;
        count++;
        return 0;
    }

    //在节点头插入
    template<class T>
    int DoubleLink<T>::insert_first(T t){
        Dnode<T> *pnode = new Dnode<T>(t, phead, phead->next);
        phead->next->prev = pnode;
        phead->next = pnode;
        count++;
        return 0;
    }

    //在节点尾插入
    template<class T>
    int DoubleLink<T>::append_last(T t){
        Dnode<T> *pnode = new Dnode<T>(t, phead, phead->next);
        phead->prev->next = pnode;
        phead->prev = pnode;
        count++;
        return 0;
    }

    //删除指定节点
    template<class T>
    int DoubleLink<T>::del(int index){
        Dnode<T> *pindex = get_index(index);
        pindex->next->prev = pindex->prev;
        pindex->prev->next = pindex->next;
        delete pindex;
        count--;
        return 0;
    }

    //删除头部节点
    template<class T>
    int DoubleLink<T>::del_first(){
        return del(0);
    }

    //删除尾部节点
    template<class T>
    int DoubleLink<T>::del_last(){
        return del(count - 1);
    }
}
#endif

View Code

 

doubleLinkTest.cpp

#include <iostream>
#include <string>
#include "doubleLink.h"

using namespace std;
using namespace DoubleLinkSpace;


// 双向链表操作int数据
void int_test()
{
    int iarr[4] = { 10, 20, 30, 40 };

    cout << "\\n----int_test----" << endl;
    // 创建双向链表
    DoubleLink<int>* pdlink = new DoubleLink<int>();

    pdlink->insert(0, 20);        // 将 20 插入到第一个位置
    pdlink->append_last(10);    // 将 10 追加到链表末尾
    pdlink->insert_first(30);    // 将 30 插入到第一个位置

    // 双向链表是否为空
    cout << "is_empty()=" << pdlink->is_empty() << endl;
    // 双向链表的大小
    cout << "size()=" << pdlink->size() << endl;

    // 打印双向链表中的全部数据
    int sz = pdlink->size();
    for (int i = 0; i<sz; i++)
        cout << "pdlink(" << i << ")=" << pdlink->get(i) << endl;
}

void string_test()
{
    string sarr[4] = { "ten", "twenty", "thirty", "forty" };

    cout << "\\n----string_test----" << endl;
    // 创建双向链表
    DoubleLink<string>* pdlink = new DoubleLink<string>();

    pdlink->insert(0, sarr[1]);        // 将 sarr中第2个元素 插入到第一个位置
    pdlink->append_last(sarr[0]);    // 将 sarr中第1个元素  追加到链表末尾
    pdlink->insert_first(sarr[2]);    // 将 sarr中第3个元素  插入到第一个位置

    // 双向链表是否为空
    cout << "is_empty()=" << pdlink->is_empty() << endl;
    // 双向链表的大小
    cout << "size()=" << pdlink->size() << endl;

    // 打印双向链表中的全部数据
    int sz = pdlink->size();
    for (int i = 0; i<sz; i++)
        cout << "pdlink(" << i << ")=" << pdlink->get(i) << endl;
}

struct stu
{
    int id;
    char name[20];
};

static stu arr_stu[] =
{
    { 10, "sky" },
    { 20, "jody" },
    { 30, "vic" },
    { 40, "dan" },
};
#define ARR_STU_SIZE ( (sizeof(arr_stu)) / (sizeof(arr_stu[0])) )

void object_test()
{
    cout << "\\n----object_test----" << endl;
    // 创建双向链表
    DoubleLink<stu>* pdlink = new DoubleLink<stu>();

    pdlink->insert(0, arr_stu[1]);        // 将 arr_stu中第2个元素 插入到第一个位置
    pdlink->append_last(arr_stu[0]);    // 将 arr_stu中第1个元素  追加到链表末尾
    pdlink->insert_first(arr_stu[2]);    // 将 arr_stu中第3个元素  插入到第一个位置

    // 双向链表是否为空
    cout << "is_empty()=" << pdlink->is_empty() << endl;
    // 双向链表的大小
    cout << "size()=" << pdlink->size() << endl;

    // 打印双向链表中的全部数据
    int sz = pdlink->size();
    struct stu p;
    for (int i = 0; i<sz; i++)
    {
        p = pdlink->get(i);
        cout << "pdlink(" << i << ")=[" << p.id << ", " << p.name << "]" << endl;
    }
}


int main()
{
    int_test();        // 演示向双向链表操作“int数据”。
    string_test();    // 演示向双向链表操作“字符串数据”。
    object_test();    // 演示向双向链表操作“对象”。

    return 0;
}

View Code

3、测试结果

----int_test----
is_empty()=0
size()=3
pdlink(0)=30
pdlink(1)=20
pdlink(2)=10

----string_test----
is_empty()=0
size()=3
pdlink(0)=thirty
pdlink(1)=twenty
pdlink(2)=ten

----object_test----
is_empty()=0
size()=3
pdlink(0)=[30, vic]
pdlink(1)=[20, jody]
pdlink(2)=[10, sky]
请按任意键继续. . .