DS05--查找

Posted 2020-11-08 李梦冰

一.学习总结

1.查找的思维导图

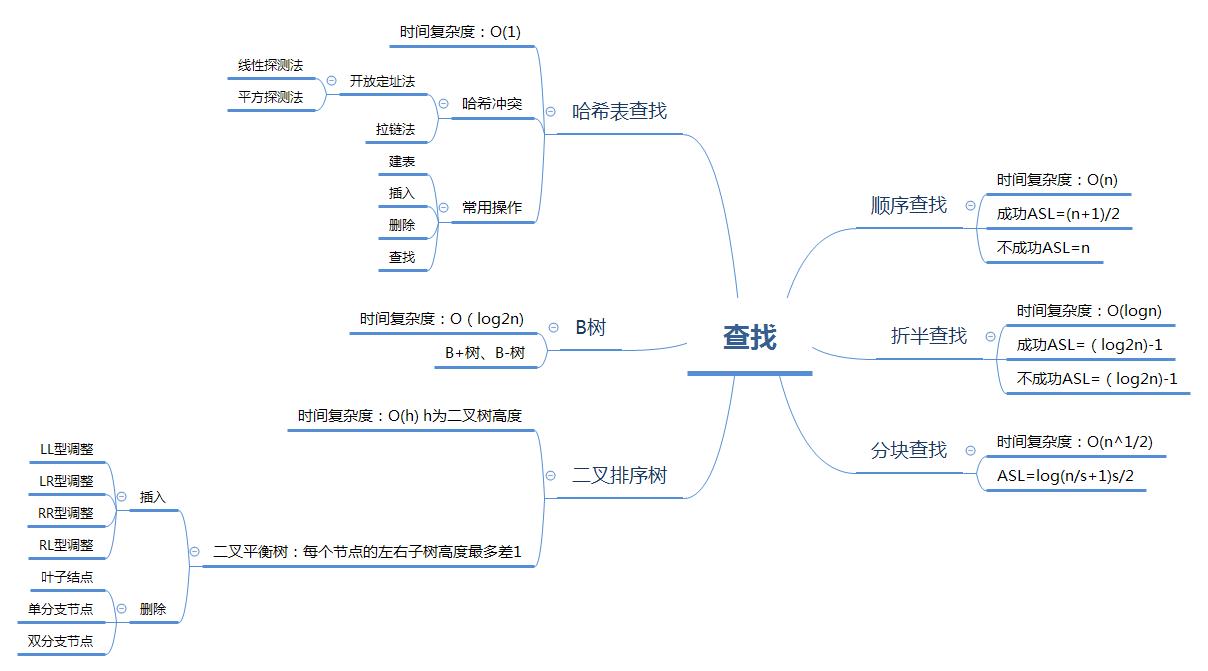
2.查找学习体会

• 2.1 关联容器和顺序容器

c++中有两种类型的容器：顺序容器和关联容器，顺序容器主要有：vector、list、deque等。其中vector表示一段连续的内存地址，基于数组的实现，list表示非连续的内存，基于链表实现。deque与vector类似，但是对于首元素提供删除和插入的双向支持。关联容器主要有map和set。map是key-value形式的，set是单值。map和set只能存放唯一的key值，multimap和multiset可以存放多个相同的key值。容器类自动申请和释放内存，我们无需new和delete操作。

• 2.2 vector(关联)

 //1.定义和初始化
     vector<int> vec1;    //默认初始化，vec1为空
     vector<int> vec2(vec1);  //使用vec1初始化vec2
     vector<int> vec3(vec1.begin(),vec1.end());//使用vec1初始化vec2
     vector<int> vec4(10);    //10个值为0的元素
     vector<int> vec5(10,4);  //10个值为4的元素
  
     //2.常用操作方法
     vec1.push_back(100);            //尾部添加元素
     int size = vec1.size();         //元素个数
     bool isEmpty = vec1.empty();    //判断是否为空
     cout<<vec1[0]<<endl;        //取得第一个元素
     vec1.insert(vec1.end(),5,3);    //从vec1.back位置插入5个值为3的元素
     vec1.pop_back();              //删除末尾元素
     vec1.erase(vec1.begin(),vec1.begin()+2);//删除vec1[0]-vec1[2]之间的元素，不包括vec1[2]其他元素前移
    cout<<(vec1==vec2)?true:false;  //判断是否相等==、！=、>=、<=...
     vector<int>::iterator iter = vec1.begin();    //获取迭代器首地址
    vector<int>::const_iterator c_iter = vec1.begin();   //获取const类型迭代器
    vec1.clear();                 //清空元素
  
     //3.遍历
     //下标法
    int length = vec1.size();
     for(int i=0;i<length;i++)
     {
        cout<<vec1[i];
     }
     cout<<endl<<endl;
     //迭代器法
    vector<int>::iterator iter = vec1.begin();
     for(;iter != vec1.end();iter++)
     {
        cout<<*iter;
     }

• 2.3 list(关联)

list是stl实现的双向链表，与向量vector想比，它允许快速的插入和删除，但是随机访问却是比较慢。

  //1.定义和初始化
    list<int> lst1;          //创建空list
    list<int> lst2(3);       //创建含有三个元素的list
    list<int> lst3(3,2); //创建含有三个元素为2的list
    list<int> lst4(lst2);    //使用lst2初始化lst4
    list<int> lst5(lst2.begin(),lst2.end());  //同lst4
 
    //2.常用操作方法
    lst1.assign(lst2.begin(),lst2.end());  //分配值,3个值为0的元素
    lst1.push_back(10);                    //末尾添加值
    lst1.pop_back();                   //删除末尾值
    lst1.begin();                      //返回首值的迭代器
    lst1.end();                            //返回尾值的迭代器
    lst1.clear();                      //清空值
    bool isEmpty1 = lst1.empty();          //判断为空
    lst1.erase(lst1.begin(),lst1.end());                        //删除元素
    lst1.front();                      //返回第一个元素的引用
    lst1.back();                       //返回最后一个元素的引用
    lst1.insert(lst1.begin(),3,2);         //从指定位置插入个3个值为2的元素
    lst1.rbegin();                         //返回第一个元素的前向指针
    lst1.remove(2);                        //相同的元素全部删除
    lst1.reverse();                        //反转
    lst1.size();                       //含有元素个数
    lst1.sort();                       //排序
    lst1.unique();                         //删除相邻重复元素
 
    //3.遍历
    //迭代器法
    for(list<int>::const_iterator iter = lst1.begin();iter != lst1.end();iter++)
    {
       cout<<*iter;
    }

• 2.4 map(顺序)

c++map容器提供一个键值对(key/value)容器，map与multimap差别仅仅在于multimap允许一个键对应多个值。对于迭代器来说，可以修改实值，而不能修改key。map会根据key自动排序.

//1.定义和初始化
    map<int,string> map1;                  //空map
   
    //2.常用操作方法
    map1[3] = "Saniya";                    //添加元素
    map1.insert(map<int,string>::value_type(2,"Diyabi"));//插入元素
    //map1.insert(pair<int,string>(1,"Siqinsini"));
    map1.insert(make_pair<int,string>(4,"V5"));
    string str = map1[3];                  //根据key取得value，key不能修改
    map<int,string>::iterator iter_map = map1.begin();//取得迭代器首地址
    int key = iter_map->first;             //取得key
    string value = iter_map->second;       //取得value
    map1.erase(iter_map);                  //删除迭代器数据
    map1.erase(3);                         //根据key删除value
    map1.size();                       //元素个数
    map1.empty();                       //判断空
    map1.clear();                      //清空所有元素
 
    //3.遍历
    for(map<int,string>::iterator iter = map1.begin();iter!=map1.end();iter++)
    {
       int keyk = iter->first;
       string valuev = iter->second;
    }

二、PTA实验作业

题目1:是否二叉搜索树

1、设计思路

定义静态全局变量最小值min
if(T为空)
	返回真
if（T不为空）
	min赋值为T的Data值
	判断T的左子树
	if（T的Data值小于min）
		返回错
	判断T的右子树

2、代码截图

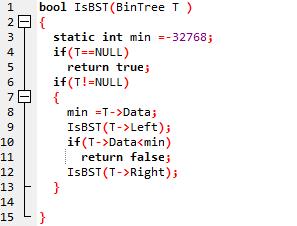
3、PTA提交列表说明

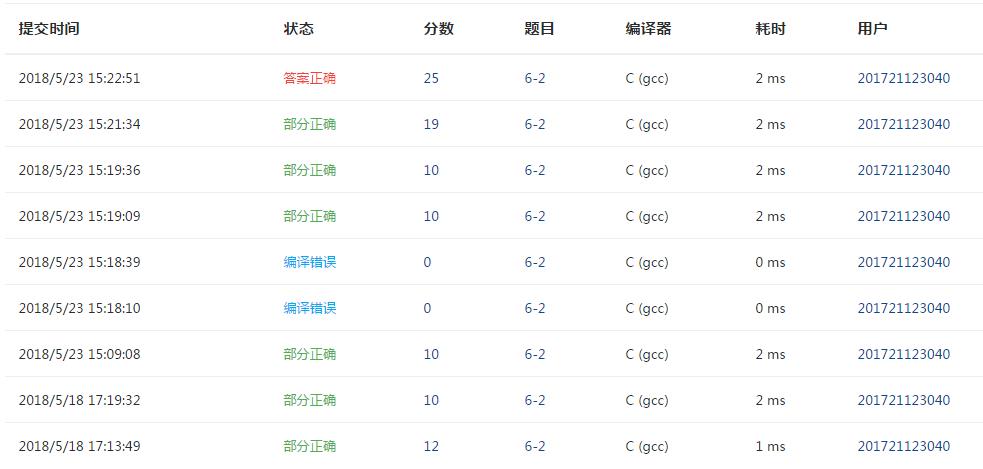
4、调试问题

- 部分正确：刚开始我是想用递归来判断每一个节点是否符合左孩子比他小，右孩子比他大这样来考虑。结果部分正确

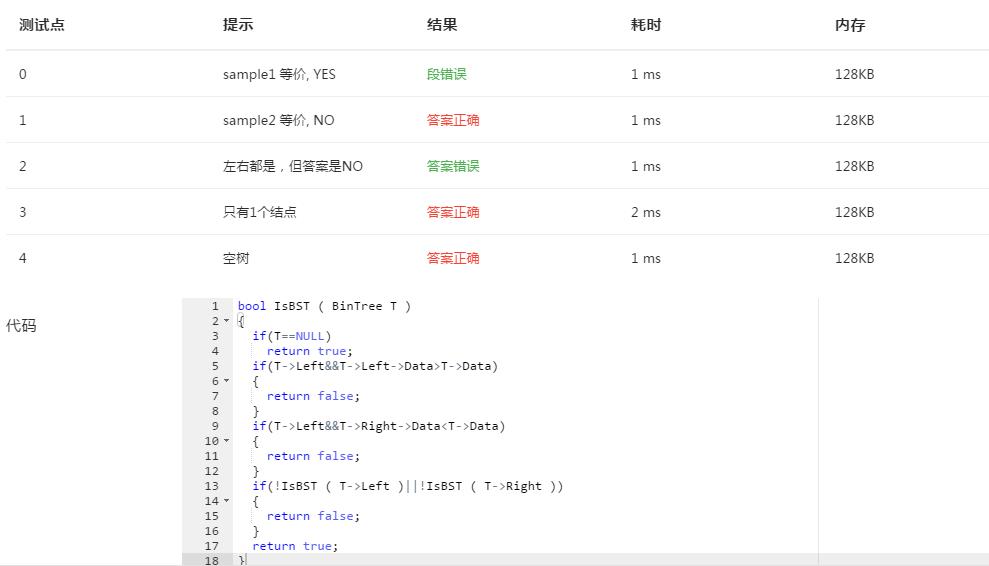
这样的错误主要是因为只能保证每个节点的都是二叉排序树，但是并没有从整体来考虑。

题目2:

1、代码截图

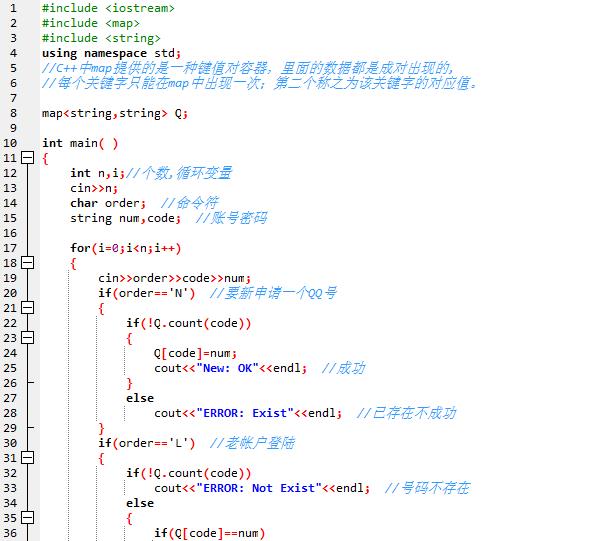
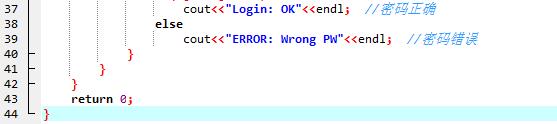
2、PTA提交列表说明

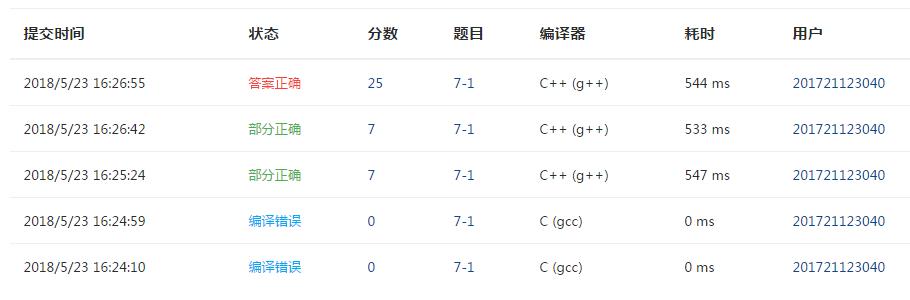
3、调试问题

本题在百度过map的用法后没有太大问题，用于记录。

题目3:

1、代码截图

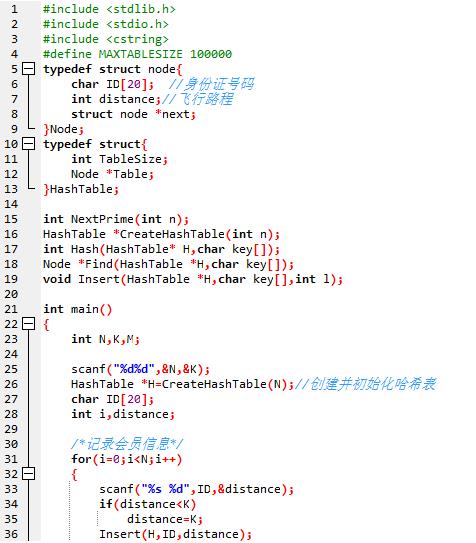
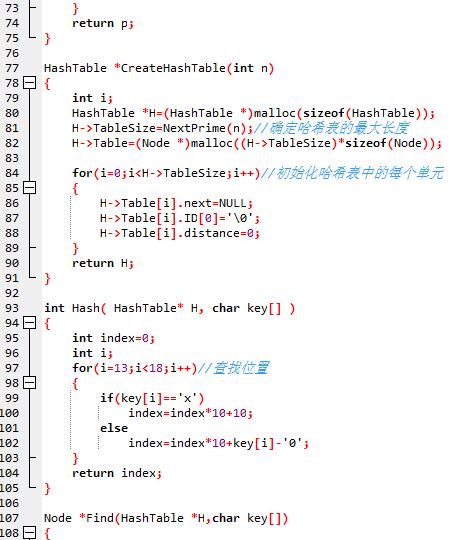
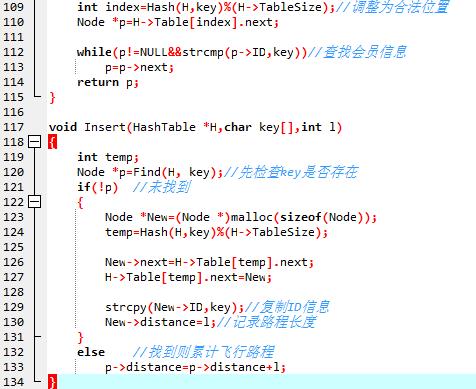
2、与优秀代码对比

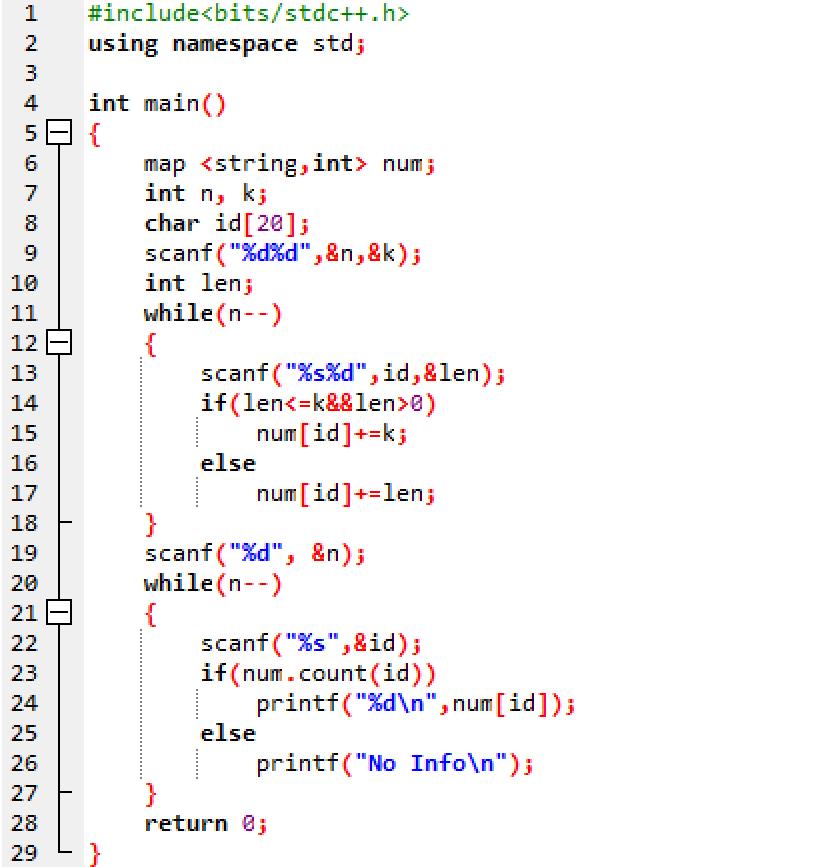
三、截图本周题目集的PTA最后排名

1、PTA排名

2、我的得分

171分

四.阅读代码：红黑树深度理解

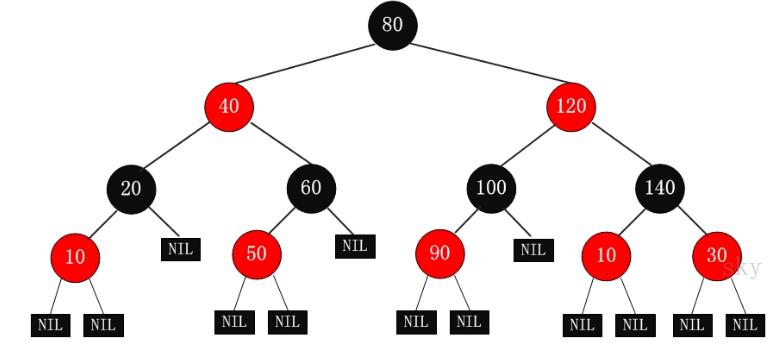
4.1 红黑树(Red-Black Tree，简称R-B Tree)

它一种特殊的二叉查找树。红黑树是特殊的二叉查找树，意味着它满足二叉查找树的特征：任意一个节点所包含的键值，大于等于左孩子的键值，小于等于右孩子的键值。除了具备该特性之外，红黑树还包括许多额外的信息。红黑树的每个节点上都有存储位表示节点的颜色，颜色是红(Red)或黑(Black)。

4.2 红黑树的特性

• 每个节点或者是黑色，或者是红色。
• 根节点是黑色。
• 每个叶子节点是黑色。
• 如果一个节点是红色的，则它的子节点必须是黑色的。
• 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

4.3 基本定义

enum RBTColor{RED, BLACK};

template <class T>
class RBTNode{
    public:
        RBTColor color;    // 颜色
        T key;            // 关键字(键值)
        RBTNode *left;    // 左孩子
        RBTNode *right;    // 右孩子
        RBTNode *parent; // 父结点

        RBTNode(T value, RBTColor c, RBTNode *p, RBTNode *l, RBTNode *r):
            key(value),color(c),parent(),left(l),right(r) {}
};

template <class T>
class RBTree {
    private:
        RBTNode<T> *mRoot;    // 根结点

    public:
        RBTree();
        ~RBTree();

        // 前序遍历"红黑树"
        void preOrder();
        // 中序遍历"红黑树"
        void inOrder();
        // 后序遍历"红黑树"
        void postOrder();

        // (递归实现)查找"红黑树"中键值为key的节点
        RBTNode<T>* search(T key);
        // (非递归实现)查找"红黑树"中键值为key的节点
        RBTNode<T>* iterativeSearch(T key);

        // 查找最小结点：返回最小结点的键值。
        T minimum();
        // 查找最大结点：返回最大结点的键值。
        T maximum();

        // 找结点(x)的后继结点。即，查找"红黑树中数据值大于该结点"的"最小结点"。
        RBTNode<T>* successor(RBTNode<T> *x);
        // 找结点(x)的前驱结点。即，查找"红黑树中数据值小于该结点"的"最大结点"。
        RBTNode<T>* predecessor(RBTNode<T> *x);

        // 将结点(key为节点键值)插入到红黑树中
        void insert(T key);

        // 删除结点(key为节点键值)
        void remove(T key);

        // 销毁红黑树
        void destroy();

        // 打印红黑树
        void print();
    private:
        // 前序遍历"红黑树"
        void preOrder(RBTNode<T>* tree) const;
        // 中序遍历"红黑树"
        void inOrder(RBTNode<T>* tree) const;
        // 后序遍历"红黑树"
        void postOrder(RBTNode<T>* tree) const;

        // (递归实现)查找"红黑树x"中键值为key的节点
        RBTNode<T>* search(RBTNode<T>* x, T key) const;
        // (非递归实现)查找"红黑树x"中键值为key的节点
        RBTNode<T>* iterativeSearch(RBTNode<T>* x, T key) const;

        // 查找最小结点：返回tree为根结点的红黑树的最小结点。
        RBTNode<T>* minimum(RBTNode<T>* tree);
        // 查找最大结点：返回tree为根结点的红黑树的最大结点。
        RBTNode<T>* maximum(RBTNode<T>* tree);

        // 左旋
        void leftRotate(RBTNode<T>* &root, RBTNode<T>* x);
        // 右旋
        void rightRotate(RBTNode<T>* &root, RBTNode<T>* y);
        // 插入函数
        void insert(RBTNode<T>* &root, RBTNode<T>* node);
        // 插入修正函数
        void insertFixUp(RBTNode<T>* &root, RBTNode<T>* node);
        // 删除函数
        void remove(RBTNode<T>* &root, RBTNode<T> *node);
        // 删除修正函数
        void removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent);

        // 销毁红黑树
        void destroy(RBTNode<T>* &tree);

        // 打印红黑树
        void print(RBTNode<T>* tree, T key, int direction);

#define rb_parent(r)   ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r)   ((r)->color==RED)
#define rb_is_black(r)  ((r)->color==BLACK)
#define rb_set_black(r)  do { (r)->color = BLACK; } while (0)
#define rb_set_red(r)  do { (r)->color = RED; } while (0)
#define rb_set_parent(r,p)  do { (r)->parent = (p); } while (0)
#define rb_set_color(r,c)  do { (r)->color = (c); } while (0)
};

4.4 左旋

/* 
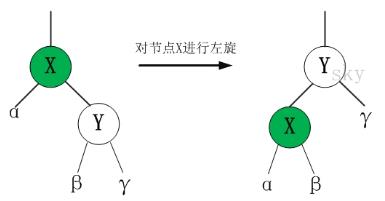
 * 对红黑树的节点(x)进行左旋转
 *
 * 左旋示意图(对节点x进行左旋)：
 *      px                              px
 *     /                               /
 *    x                               y                
 *   /  \\      --(左旋)-->           / \\                #
 *  lx   y                          x  ry     
 *     /   \\                       /  \\
 *    ly   ry                     lx  ly  
 *
 *
 */
template <class T>
void RBTree<T>::leftRotate(RBTNode<T>* &root, RBTNode<T>* x)
{
    // 设置x的右孩子为y
    RBTNode<T> *y = x->right;

    // 将 “y的左孩子” 设为 “x的右孩子”；
    // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
    x->right = y->left;
    if (y->left != NULL)
        y->left->parent = x;

    // 将 “x的父亲” 设为 “y的父亲”
    y->parent = x->parent;

    if (x->parent == NULL)
    {
        root = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
    }
    else
    {
        if (x->parent->left == x)
            x->parent->left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x->parent->right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    }
    
    // 将 “x” 设为 “y的左孩子”
    y->left = x;
    // 将 “x的父节点” 设为 “y”
    x->parent = y;
}

4.5 右旋

/* 
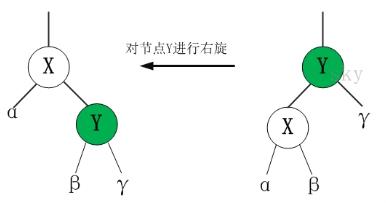
 * 对红黑树的节点(y)进行右旋转
 *
 * 右旋示意图(对节点y进行左旋)：
 *            py                               py
 *           /                                /
 *          y                                x                  
 *         /  \\      --(右旋)-->            /  \\                     #
 *        x   ry                           lx   y  
 *       / \\                                   / \\                   #
 *      lx  rx                                rx  ry
 * 
 */
template <class T>
void RBTree<T>::rightRotate(RBTNode<T>* &root, RBTNode<T>* y)
{
    // 设置x是当前节点的左孩子。
    RBTNode<T> *x = y->left;

    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y->left = x->right;
    if (x->right != NULL)
        x->right->parent = y;

    // 将 “y的父亲” 设为 “x的父亲”
    x->parent = y->parent;

    if (y->parent == NULL) 
    {
        root = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
    }
    else
    {
        if (y == y->parent->right)
            y->parent->right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y->parent->left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }

    // 将 “y” 设为 “x的右孩子”
    x->right = y;

    // 将 “y的父节点” 设为 “x”
    y->parent = x;
}

五. 代码Git提交记录截图