SSE图像算法优化系列十八：三次卷积插值的进一步SSE优化。

Posted 2020-11-07 只(挚)爱图像处理

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了SSE图像算法优化系列十八：三次卷积插值的进一步SSE优化。相关的知识，希望对你有一定的参考价值。

　　本文是在学习https://blog.csdn.net/housisong/article/details/1452249一文的基础上对算法的理解和重新整理，再次非常感谢原文作者的深入分析以及分享。

　　三次卷积插值的基础原理也是对取样点附近的领域像素按照某种权重分布计算加权的结果值，比起双线性的4个领域像素计算，三次卷积涉及到了16个领域像素，这也决定了其取样点位置不是对称的，同时耗时比双线性也大为增加。

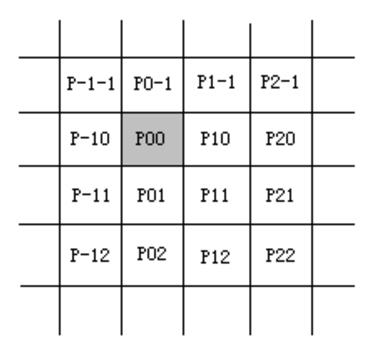
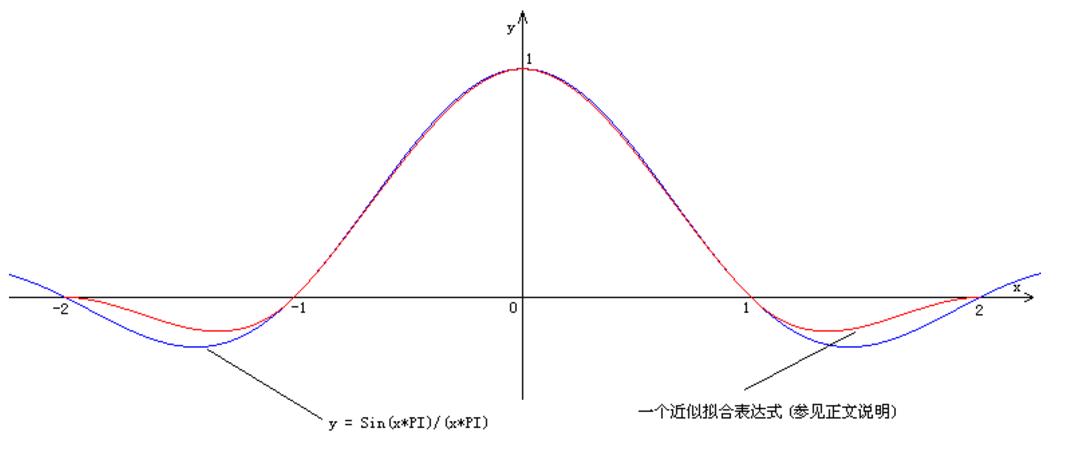
如左图所示，P00为向下取整后的取样点的坐标，其领域16个像素的位置整体靠取样点的右下侧，各个位置的重系数并不是固定值，而是和取样点的浮点坐标的小数部分关。其值由函数Sin(x * pi) / (x * pi)决定，该函数曲线如右图蓝色曲线所示，当小数部分假定为U时，在水平或者垂直方向的4个权重分量对应的x值分别为：1+U、U、1-U以及2-U。

　　实际的操作中，我们常常用一个拟合的表达式来近似该曲线，比如原文作者提供的如下代码：

float SinXDivX(float X)
{
    const float a = -1;                    //    a还可以取 a=-2,-1,-0.75,-0.5等等，起到调节锐化或模糊程度的作用
    X = abs(X);
    float X2 = X * X, X3 = X2 * X;
    if (X <= 1)
        return (a + 2) * X3 - (a + 3) * X2 + 1;
    else if (X <= 2)
        return a * X3 - (5 * a) * X2 + (8 * a) * X - (4 * a);
    else
        return 0;
}

　　标准的函数应该是：

float SinXDivX_Standard(float X)
{
    if (abs(X) < 0.000001f)
        return 1;
    else
        return sin(X * 3.1415926f) / (X * 3.1415926f);
}

　　注意到一点，比如X取值为0.3，如果按照标准函数

　　　　SinXDivX_Standard(1 + X) + SinXDivX_Standard(X) + SinXDivX_Standard(1 - X) + SinXDivX_Standard(2 - X) = 0.8767

　　但是如果是下式：　　

SinXDivX(1 + X) + SinXDivX(X) + SinXDivX(1 - X) + SinXDivX(2 - X) 则等于1。

　　所以使用拟合式的好处就是权重系数之后无需在进行归一化的处理了。

　　对于一个浮点的映射坐标，使用三次卷积插值的简单的代码如下所示：

void Bicubic_Original(unsigned char *Src, int Width, int Height, int Stride, unsigned char *Pixel, float X, float Y)
{
    int Channel = Stride / Width;
    int PosX = floor(X), PosY = floor(Y);
    float PartXX = X - PosX, PartYY = Y - PosY;

    unsigned char *Pixel00 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY - 1);
    unsigned char *Pixel01 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY - 1);
    unsigned char *Pixel02 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY - 1);
    unsigned char *Pixel03 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY - 1);
    unsigned char *Pixel10 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 0);
    unsigned char *Pixel11 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 0);
    unsigned char *Pixel12 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 0);
    unsigned char *Pixel13 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 0);
    unsigned char *Pixel20 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 1);
    unsigned char *Pixel21 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 1);
    unsigned char *Pixel22 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 1);
    unsigned char *Pixel23 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 1);
    unsigned char *Pixel30 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 2);
    unsigned char *Pixel31 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 2);
    unsigned char *Pixel32 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 2);
    unsigned char *Pixel33 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 2);

    float U0 = SinXDivX(1 + PartXX), U1 = SinXDivX(PartXX);
    float U2 = SinXDivX(1 - PartXX), U3 = SinXDivX(2 - PartXX);
    float V0 = SinXDivX(1 + PartYY), V1 = SinXDivX(PartYY);
    float V2 = SinXDivX(1 - PartYY), V3 = SinXDivX(2 - PartYY);

    for (int I = 0; I < Channel; I++)
    {
        float Sum1 = (Pixel00[I] * U0 + Pixel01[I] * U1 + Pixel02[I] * U2 + Pixel03[I] * U3) * V0;
        float Sum2 = (Pixel10[I] * U0 + Pixel11[I] * U1 + Pixel12[I] * U2 + Pixel13[I] * U3) * V1;
        float Sum3 = (Pixel20[I] * U0 + Pixel21[I] * U1 + Pixel22[I] * U2 + Pixel23[I] * U3) * V2;
        float Sum4 = (Pixel30[I] * U0 + Pixel31[I] * U1 + Pixel22[I] * U2 + Pixel33[I] * U3) * V3;
        Pixel[I] = IM_ClampToByte(Sum1 + Sum2 + Sum3 + Sum4 + 0.5f);
    }
}

　　其中GetCheckedPixel为简单的取像素值的函数。

inline unsigned char *GetCheckedPixel(unsigned char *Src, int Width, int Height, int Stride, int Channel, int PosX, int PosY)
{
    return Src + IM_ClampI(PosY, 0, Height - 1) * Stride + IM_ClampI(PosX, 0, Width - 1) * Channel;
}

　　参考作者的源代码，一个最直接的三次卷积插值的函数如下所示：

int IM_Resample_Original(unsigned char *Src, unsigned char *Dest, int SrcW, int SrcH, int StrideS, int DstW, int DstH, int StrideD, int InterpolationMode)
{
    int Channel = StrideS / SrcW;
    if ((Src == NULL) || (Dest == NULL))                                return IM_STATUS_NULLREFRENCE;
    if ((SrcW <= 0) || (SrcH <= 0) || (DstW <= 0) || (DstH <= 0))        return IM_STATUS_INVALIDPARAMETER;
    if ((Channel != 1) && (Channel != 3) && (Channel != 4))                return IM_STATUS_INVALIDPARAMETER;

    if ((SrcW == DstW) && (SrcH == DstH))
    {
        memcpy(Dest, Src, SrcW * SrcH * Channel * sizeof(unsigned char));
        return IM_STATUS_OK;
    }

    //    已经论证这个没有必要用SSE去做优化，速度不会有太大的变化， 2018.3.28
    if (InterpolationMode == 0)                            // 最近邻插值
    {

    }
    else if (InterpolationMode == 1)                    　　//    双线性插值方式
    {

    }
    else if (InterpolationMode == 2)            　　　　　　//    三次立方插值
    {
        for (int Y = 0; Y < DstH; Y++)
        {
            unsigned char *LinePD = Dest + Y * StrideD;
            float SrcY = (Y + 0.4999999f) * SrcH / DstH - 0.5f;
            for (int X = 0; X < DstW; X++)
            {
                float SrcX = (X + 0.4999999f) * SrcW / DstW - 0.5f;
                Bicubic_Original(Src, SrcW, SrcH, StrideS, LinePD, SrcX, SrcY);
                LinePD += Channel;
            }    
        }
    }
    return IM_STATUS_OK;
}

　　这个速度是非常缓慢的，因为有大量的浮点计算和坐标位置计算。

　　为了提高速度，原文的作者对该算法进行了大量的优化，主要包括（1）使用定点数来优化缩放函数；（2）边界和内部分开处理；（3）对SinXDivX做一个查找表；（4）对border_color做一个查找表，我按照我自己的思路进一步整理成了我比较熟悉的代码格式，主要如下片段所示：

//    边界处的三次立方插值
__forceinline void Bicubic_Border(unsigned char *Src, int Width, int Height, int Stride, unsigned char *Pixel, short *SinXDivX_Table, int SrcX, int SrcY)
{
    int Channel = Stride / Width;
    int U = (unsigned char)(SrcX >> 8), V = (unsigned char)(SrcY >> 8);

    int U0 = SinXDivX_Table[256 + U], U1 = SinXDivX_Table[U];
    int U2 = SinXDivX_Table[256 - U], U3 = SinXDivX_Table[512 - U];
    int V0 = SinXDivX_Table[256 + V], V1 = SinXDivX_Table[V];
    int V2 = SinXDivX_Table[256 - V], V3 = SinXDivX_Table[512 - V];
    int PosX = SrcX >> 16, PosY = SrcY >> 16;

    unsigned char *Pixel00 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY - 1);
    unsigned char *Pixel01 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY - 1);
    unsigned char *Pixel02 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY - 1);
    unsigned char *Pixel03 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY - 1);
    unsigned char *Pixel10 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 0);
    unsigned char *Pixel11 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 0);
    unsigned char *Pixel12 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 0);
    unsigned char *Pixel13 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 0);
    unsigned char *Pixel20 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 1);
    unsigned char *Pixel21 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 1);
    unsigned char *Pixel22 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 1);
    unsigned char *Pixel23 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 1);
    unsigned char *Pixel30 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX - 1, PosY + 2);
    unsigned char *Pixel31 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 0, PosY + 2);
    unsigned char *Pixel32 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 1, PosY + 2);
    unsigned char *Pixel33 = GetCheckedPixel(Src, Width, Height, Stride, Channel, PosX + 2, PosY + 2);

    for (int I = 0; I < Channel; I++)
    {
        int Sum1 = (Pixel00[I] * U0 + Pixel01[I] * U1 + Pixel02[I] * U2 + Pixel03[I] * U3) * V0;
        int Sum2 = (Pixel10[I] * U0 + Pixel11[I] * U1 + Pixel12[I] * U2 + Pixel13[I] * U3) * V1;
        int Sum3 = (Pixel20[I] * U0 + Pixel21[I] * U1 + Pixel22[I] * U2 + Pixel23[I] * U3) * V2;
        int Sum4 = (Pixel30[I] * U0 + Pixel31[I] * U1 + Pixel22[I] * U2 + Pixel33[I] * U3) * V3;
        Pixel[I] = IM_ClampToByte((Sum1 + Sum2 + Sum3 + Sum4) >> 16);
    }
}

//    __forceinline强制内联还是能提高点速度的，毕竟这个函数的参数很多
//    如果是确定的通道数，可以把里面的Channel改为固定的值，速度能提高很多
__forceinline void Bicubic_Center(unsigned char *Src, int Width, int Height, int Stride, unsigned char *Pixel, short *SinXDivX_Table, int SrcX, int SrcY)
{
    int Channel = Stride / Width;
    int U = (unsigned char)(SrcX >> 8), V = (unsigned char)(SrcY >> 8);

    int U0 = SinXDivX_Table[256 + U], U1 = SinXDivX_Table[U];
    int U2 = SinXDivX_Table[256 - U], U3 = SinXDivX_Table[512 - U];
    int V0 = SinXDivX_Table[256 + V], V1 = SinXDivX_Table[V];
    int V2 = SinXDivX_Table[256 - V], V3 = SinXDivX_Table[512 - V];
    int PosX = SrcX >> 16, PosY = SrcY >> 16;

    unsigned char *Pixel00 = Src + (PosY - 1) * Stride + (PosX - 1) * Channel;
    unsigned char *Pixel01 = Pixel00 + Channel;
    unsigned char *Pixel02 = Pixel01 + Channel;
    unsigned char *Pixel03 = Pixel02 + Channel;
    unsigned char *Pixel10 = Pixel00 + Stride;
    unsigned char *Pixel11 = Pixel10 + Channel;
    unsigned char *Pixel12 = Pixel11 + Channel;
    unsigned char *Pixel13 = Pixel12 + Channel;
    unsigned char *Pixel20 = Pixel10 + Stride;
    unsigned char *Pixel21 = Pixel20 + Channel;
    unsigned char *Pixel22 = Pixel21 + Channel;
    unsigned char *Pixel23 = Pixel22 + Channel;
    unsigned char *Pixel30 = Pixel20 + Stride;
    unsigned char *Pixel31 = Pixel30 + Channel;
    unsigned char *Pixel32 = Pixel31 + Channel;
    unsigned char *Pixel33 = Pixel32 + Channel;
    for (int I = 0; I < Channel; I++)
    {
        int Sum1 = (Pixel00[I] * U0 + Pixel01[I] * U1 + Pixel02[I] * U2 + Pixel03[I] * U3) * V0;
        int Sum2 = (Pixel10[I] * U0 + Pixel11[I] * U1 + Pixel12[I] * U2 + Pixel13[I] * U3) * V1;
        int Sum3 = (Pixel20[I] * U0 + Pixel21[I] * U1 + Pixel22[I] * U2 + Pixel23[I] * U3) * V2;
        int Sum4 = (Pixel30[I] * U0 + Pixel31[I] * U1 + Pixel22[I] * U2 + Pixel33[I] * U3) * V3;
        Pixel[I] = IM_ClampToByte((Sum1 + Sum2 + Sum3 + Sum4) >> 16);
    }
}

int IM_Resample_PureC(unsigned char *Src, unsigned char *Dest, int SrcW, int SrcH, int StrideS, int DstW, int DstH, int StrideD, int InterpolationMode)
{
    int Channel = StrideS / SrcW;
    if ((Src == NULL) || (Dest == NULL))                                return IM_STATUS_NULLREFRENCE;
    if ((SrcW <= 0) || (SrcH <= 0) || (DstW <= 0) || (DstH <= 0))        return IM_STATUS_INVALIDPARAMETER;
    if ((Channel != 1) && (Channel != 3) && (Channel != 4))                return IM_STATUS_INVALIDPARAMETER;

    if ((SrcW == DstW) && (SrcH == DstH))
    {
        memcpy(Dest, Src, SrcW * SrcH * Channel * sizeof(unsigned char));
        return IM_STATUS_OK;
    }

    //    已经论证这个没有必要用SSE去做优化，速度不会有太大的变化， 2018.3.28
    if (InterpolationMode == 0)                            // 最近邻插值
    {

    }
    else if (InterpolationMode == 1)                    //    双线性插值方式
    {

    }
    else if (InterpolationMode == 2)            //    三次立方插值
    {
        short *SinXDivX_Table = (short *)malloc(513 * sizeof(short));
        if (SinXDivX_Table == NULL)
        {
            if (SinXDivX_Table != NULL)        free(SinXDivX_Table);
            return IM_STATUS_NULLREFRENCE;
        }
        for (int I = 0; I < 513; I++)
            SinXDivX_Table[I] = int(0.5 + 256 * SinXDivX(I / 256.0f));            //    建立查找表，定点化

        int AddX = (SrcW << 16) / DstW, AddY = (SrcH << 16) / DstH;
        int ErrorX = -(1 << 15) + (AddX >> 1), ErrorY = -(1 << 15) + (AddY >> 1);

        int StartX = ((1 << 16) - ErrorX) / AddX + 1;            //    计算出需要特殊处理的边界
        int StartY = ((1 << 16) - ErrorY) / AddY + 1;            //    y0+y*yr>=1; y0=ErrorY => y>=(1-ErrorY)/yr
        int EndX = (((SrcW - 3) << 16) - ErrorX) / AddX + 1;
        int EndY = (((SrcH - 3) << 16) - ErrorY) / AddY + 1;    //    y0+y*yr<=(height-3) => y<=(height-3-ErrorY)/yr
        if (StartY >= DstH)            StartY = DstH;
        if (StartX >= DstW)            StartX = DstW;
        if (EndX < StartX)            EndX = StartX;
        if (EndY < StartY)            EndY = StartY;

        int SrcY = ErrorY;
        for (int Y = 0; Y < StartY; Y++, SrcY += AddY)            //    前面的不是都有效的取样部分数据
        {
            unsigned char *LinePD = Dest + Y * StrideD;
            for (int X = 0, SrcX = ErrorX; X < DstW; X++, SrcX += AddX, LinePD += Channel)
            {
                Bicubic_Border(Src, SrcW, SrcH, StrideS, LinePD, SinXDivX_Table, SrcX, SrcY);
            }
        }
        for (int Y = StartY; Y < EndY; Y++, SrcY += AddY)
        {
            int SrcX = ErrorX;
            unsigned char *LinePD = Dest + Y * StrideD;
            for (int X = 0; X < StartX; X++, SrcX += AddX, LinePD += Channel)
            {
                Bicubic_Border(Src, SrcW, SrcH, StrideS, LinePD, SinXDivX_Table, SrcX, SrcY);
            }
            for (int X = StartX; X < EndX; X++, SrcX += AddX, LinePD += Channel)
            {
                Bicubic_Center(Src, SrcW, SrcH, StrideS, LinePD, SinXDivX_Table, SrcX, SrcY);
            }
            for (int X = EndX; X < DstW; X++, SrcX += AddX, LinePD += Channel)
            {
                Bicubic_Border(Src, SrcW, SrcH, StrideS, LinePD, SinXDivX_Table, SrcX, SrcY);
            }
        }
        for (int Y = EndY; Y < DstH; Y++, SrcY += AddY)
        {
            unsigned char *LinePD = Dest + Y * StrideD;
            for (int X = 0, SrcX = ErrorX; X < DstW; X++, SrcX += AddX, LinePD += Channel)
            {
                Bicubic_Border(Src, SrcW, SrcH, StrideS, LinePD, SinXDivX_Table, SrcX, SrcY);
            }
        }
        free(SinXDivX_Table);
    }
    return IM_STATUS_OK;
}

　　用于Bicubic_Border 和Bicubic_Center在函数中大量的被调用，函数的调用开销也是不可忽略的，在VS中可以用__forceinline来进行强制内联，这个大约对本例大约有10%的提速效果。

　　本例的Bicubic_Border 和Bicubic_Center函数是为了通用不同通道，用了一个for循环，实际操作时为了效率应该要分通道展开的，展开后的效率约能提高30%。

　　以上纯C代码将32位的800*600的代码放大到1024*768大约需要40ms(如果通道分开写，大约需要30ms)。

　　为了进一步提高速度，我们来考虑这个算法的SSE优化，在HouSisong的专栏里已经有了SSE优化的代码，不过他时直接内嵌汇编写的，比较难以看懂，并且现在的64位操作系统时无法内嵌汇编的了，但是还是可以使用intrinsic，所以这里我使用intrinsic语句来处理（其实我也没看懂HouSisong的代码）。

　　对于边缘部分，计算量不大，直接使用C版本的Bicubic_Border函数，重点我们看看Bicubic_Center函数。

　　Bicubic_Center函数前面部分的代码主要时计算权重系数和取样点的内存坐标，先不管，我们看看核心的计算部分代码如下：

    for (int I = 0; I < Channel; I++)
    {
        int Sum1 = (Pixel00[I] * U0 + Pixel01[I] * U1 + Pixel02[I] * U2 + Pixel03[I] * U3) * V0;　　　　//　　行1
        int Sum2 = (Pixel10[I] * U0 + Pixel11[I] * U1 + Pixel12[I] * U2 + Pixel13[I] * U3) * V1;　　　　//　　行2
        int Sum3 = (Pixel20[I] * U0 + Pixel21[I] * U1 + Pixel22[I] * U2 + Pixel23[I] * U3) * V2;　　　　//　　行3
        int Sum4 = (Pixel30[I] * U0 + Pixel31[I] * U1 + Pixel22[I] * U2 + Pixel33[I] * U3) * V3;　　　　//　　行4
        Pixel[I] = IM_ClampToByte((Sum1 + Sum2 + Sum3 + Sum4) >> 16);
    }

　　先考虑Channel为1的情况，观察这一句：Pixel00[I] * U0 + Pixel01[I] * U1 + Pixel02[I] * U2 + Pixel03[I] * U3，注意此时Pixel00/Pixel01/Pixel02/Pixel03在内存中是连续的，而且取值范围在[0,255]之间，U0/U1/U2/U3根据前面的查找表建立过程，也在[0,256]之间，他们都能用short类型来表达，而这个式子为连乘然后累加，我们考虑使用一个特殊的SSE指令_mm_madd_epi16，在MSDN中其功能解释如下：

Multiplies the 8 signed 16-bit integers from a by the 8 signed 16-bit integers from b.

  __m128i _mm_madd_epi16 (__m128i a, __m128i b);

Return Value

　 Adds the signed 32-bit integer results pairwise and packs the 4 signed 32-bit integer results.

　　r0 := (a0 * b0) + (a1 * b1)
　　r1 := (a2 * b2) + (a3 * b3)
　　r2 := (a4 * b4) + (a5 * b5)
　　r3 := (a6 * b6) + (a7 * b7)

　即a和b里分别有8个有符号的16位数，然后对应的16位数据两两相乘，然后在两两相加，最后保存到4个32位有符号数中。

　考虑我们的应用场景，行1到行4每行的代码都只有4次乘法和3次加法，不能直接使用，但是我们可以考虑把两行整合在一起，一次性计算，这样就需要调用2次

_mm_madd_epi16 ，然后2次的结果在调用_mm_hadd_epi32这个水平方向的累加函数就能得到新的结果，感觉真的有点奇妙，核心代码如下所示：

　　if (Channel == 1)
    {
        __m128i P01 = _mm_cvtepu8_epi16(_mm_unpacklo_epi32(_mm_cvtsi32_si128(*((int *)Pixel0)), _mm_cvtsi32_si128(*((int *)Pixel1))));            //    P00 P01 P02 P03 P10 P11 P12 P13
        __m128i P23 = _mm_cvtepu8_epi16(_mm_unpacklo_epi32(_mm_cvtsi32_si128(*((int *)Pixel2)), _mm_cvtsi32_si128(*((int *)Pixel3))));            //    P20 P21 P22 P23 P30 P31 P32 P33
        __m128i Sum01 = _mm_madd_epi16(P01, PartX);                            // P00 * U0 + P01 * U1        P02 * U2 + P03 * U3         P10 * U0 + P11 * U1        P12 * U2 + P13 * U3
        __m128i Sum23 = _mm_madd_epi16(P23, PartX);                            // P20 * U0 + P21 * U1        P22 * U2 + P23 * U3         P30 * U0 + P31 * U1        P32 * U2 + P33 * U3
        __m128i Sum = _mm_hadd_epi32(Sum01, Sum23);                            // P00 * U0 + P01 * U1 + P02 * U2 + P03 * U3     P10 * U0 + P11 * U1 + P12 * U2 + P13 * U3    P20 * U0 + P21 * U1    + P22 * U2 + P23 * U3    P30 * U0 + P31 * U1 + P32 * U2 + P33 * U3
        LinePD[0] = IM_ClampToByte(_mm_hsum_epi32(_mm_mullo_epi32(Sum, PartY)) >> 16);
    }

其中_mm_hsum_epi32为自定义的一个函数。

//    4个有符号的32位的数据相加的和。
inline int _mm_hsum_epi32(__m128i V)                        //    V3 V2 V1 V0
{
    //    实测这个速度要快些，_mm_extract_epi32最慢。
    __m128i T = _mm_add_epi32(V, _mm_srli_si128(V, 8));        //    V3+V1            V2+V0        V1        V0        
    T = _mm_add_epi32(T, _mm_srli_si128(T, 4));                //    V3+V1+V2+V0        V2+V0+V1    V1+V0    V0    
    return _mm_cvtsi128_si32(T);                            //    提取低位    
}

　　我感觉有的时候这些东西用语言是无法能明确而有效的表达的，而直接用代码却能达到事半功倍的效果。

　　前面已经测试过用拟合曲线那个公式能满足累加和正好为一，而不需要归一化的，那么理论上这个最后的移位操作后数据应该就在【0，255】范围内，而不需要进行Clamp的，但是实际如果没有这个Clamp，结果图像会有部分像素溢出的，这是因为在我们定点化的过程中，这个和为1的特性已经遭到了一定的破坏了。

　　注意在Bicubic_Center的循环计算中，V分量在计算每行时是固定的，每行开始时可以直接一次使用_mm_setr_epi32来设置，，U分量计算每行时对于每个像素都是变化的，我们可以对每个像素用_mm_setr_epi32来设置，但是多次使用这个intrinsic是个比较耗时的过程，因此我们应该把每行的U保存到一个临时内存中，然后每次使用时从不同的Load方可提高速度。

　　当不是单通道的图像时，比如4通道，优化的思路是相同的，只不过我们需要做更多的拆分和组合工作，把原始的数据组合成符合SIMD指令需要的格式，这就需要灵活的使用_mm_shuffle_epi8、_mm_unpacklo_epi32、_mm_unpackhi_epi32、_mm_unpacklo_epi8、_mm_unpacklo_epi8等语句的组合，这些语句都是非常快速和高效的，对于32位图像，由于一次性可以处理4个字节，最后的IM_ClampToByte还可以直接使用SIMD的抗饱和指令（_mm_packus_epi32）代替，效率能提高少许，而且还可以调用不进行缓存的_mm_stream_si32指令直接写内存，因此能极大的提高效率。具体的组合代码请参考本文附件。

　　最后贴出基于SSE优化的代码：

int IM_Resample_SSE(unsigned char *Src, unsigned char *Dest, int SrcW, int SrcH, int StrideS, int DstW, int DstH, int StrideD, int InterpolationMode)
{
    int Channel = StrideS / SrcW;
    if ((Src == NULL) || (Dest == NULL))                                return IM_STATUS_NULLREFRENCE;
    if ((SrcW <= 0) || (SrcH <= 0) || (DstW <= 0) || (DstH <= 0))        return IM_STATUS_INVALIDPARAMETER;
    if ((Channel != 1) && (Channel != 3) && (Channel != 4))                return IM_STATUS_INVALIDPARAMETER;

    if ((SrcW == DstW) && (SrcH == DstH))
    {
        memcpy(Dest, Src, SrcW * SrcH * Channel * sizeof(unsigned char));
        return IM_STATUS_OK;
    }

    //    已经论证这个没有必要用SSE去做优化，速度不会有太大的变化， 2018.3.28
    if (InterpolationMode == 0)                            // 最近邻插值
    {

    }
    else if (InterpolationMode == 1)                    //    双线性插值方式
    {

    }
    else if (InterpolationMode == 2)            //    三次立方插值
    {
        short *SinXDivX_Table = (short *)malloc(513 * sizeof(short));
        short *Table = (short *)malloc(DstW * 4 * sizeof(short));
        if ((SinXDivX_Table == NULL) || (Table == NULL))
        {
            if (SinXDivX_Table != NULL)        free(SinXDivX_Table);
            if (Table != NULL)                free(Table);
            return IM_STATUS_NULLREFRENCE;
        }
        for (int I = 0; I < 513; I++)
            SinXDivX_Table[I] = int(0.5 + 256 * SinXDivX(I / 256.0f));            //    建立查找表，定点化

        int AddX = (SrcW << 16) / DstW, AddY = (SrcH << 16) / DstH;
        int ErrorX = -(1 << 15) + (AddX >> 1), ErrorY = -(1 << 15) + (AddY >> 1);

        int StartX = ((1 << 16) - ErrorX) / AddX + 1;       以上是关于SSE图像算法优化系列十八：三次卷积插值的进一步SSE优化。的主要内容，如果未能解决你的问题，请参考以下文章 
 SSE图像算法优化系列二十二：优化龚元浩博士的曲率滤波算法，达到约500 MPixels/Sec的单次迭代速度。
 SSE图像算法优化系列十：简单的一个肤色检测算法的SSE优化。
 漫步最优化二十八——三次插值法
 SSE图像算法优化系列三十一：Base64编码和解码算法的指令集优化（C#自带函数的3到4倍速度）。
 SSE图像算法优化系列二十四: 基于形态学的图像后期抗锯齿算法--MLAA优化研究。
 SSE图像算法优化系列二十四: 基于形态学的图像后期抗锯齿算法--MLAA优化研究。