闭关修炼 动态规划1——最长公共子序列(UVA111)

Posted 2020-07-11

 

一： 作用

       最长公共子序列的问题常用于解决字符串的相似度，是一个非常实用的算法，作为码农，此算法是我们的必备基本功。

二：概念

     举个例子，cnblogs这个字符串中子序列有多少个呢？很显然有2⁷个，比如其中的cb,cgs等等都是其子序列，我们可以看出

子序列不见得一定是连续的，连续的那是子串。

     我想大家已经了解了子序列的概念，那现在可以延伸到两个字符串了，那么大家能够看出：cnblogs和belong的公共子序列吗？

在你找出的公共子序列中，你能找出最长的公共子序列吗？

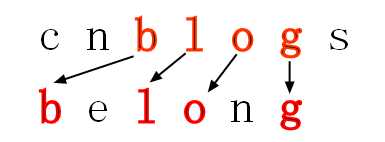
从图中我们看到了最长公共子序列为blog，仔细想想我们可以发现其实最长公共子序列的个数不是唯一的，可能会有两个以上，

但是长度一定是唯一的，比如这里的最长公共子序列的长度为4。

 

三：解决方案

<1> 枚举法

       这种方法是最简单，也是最容易想到的，当然时间复杂度也是龟速的，我们可以分析一下，刚才也说过了cnblogs的子序列

个数有2⁷个 ，延伸一下：一个长度为N的字符串，其子序列有2^N个，每个子序列要在第二个长度为N的字符串中去匹配，匹配一次

需要O(N)的时间，总共也就是O(N*2^N)，可以看出，时间复杂度为指数级，恐怖的令人窒息。

 

<2> 动态规划

      既然是经典的题目肯定是有优化空间的，并且解题方式是有固定流程的，这里我们采用的是矩阵实现，也就是二维数组。

第一步：先计算最长公共子序列的长度。

第二步：根据长度，然后通过回溯求出最长公共子序列。

现有两个序列X={x₁,x₂,x_3，...x_i}，Y={y₁,y₂,y_3，....，y_i}，

设一个C[i,j]: 保存X_i与Y_j的LCS的长度。

递推方程为：

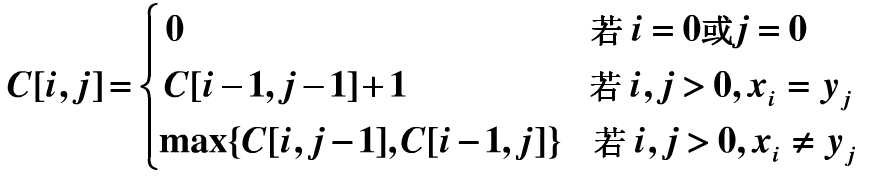
不知道大家看懂了没？动态规划的一个重要性质特点就是解决“子问题重叠”的场景，可以有效的避免重复计算，根据上面的

公式其实可以发现C[i,j]一直保存着当前(X_i,Y_i)的最大子序列长度。

 

题目：不赘述，模板题

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
using namespace std;


int dp[25][25];
int a[25];
int x[25];
int main()
{
	int n,i,j;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		int b;
		scanf("%d",&b);
		a[b]=i;
	}

	int t;
	while(scanf("%d",&t)!=EOF)
	{
		x[t]=1;
		for(i=2;i<=n;i++)
		{
			int b;
			scanf("%d",&b);
			x[b]=i;
		}

		memset(dp,0,sizeof(dp));
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=n;j++)
			{
				if(a[i]==x[j])
					dp[i][j]=dp[i-1][j-1]+1;
				else
					dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
			}
		}

		printf("%d\\n",dp[n][n]);
	}
	return 0;
}