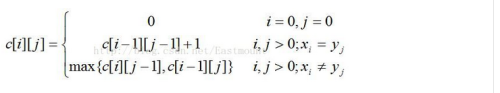动态规划-最长公共子序列

Posted 2020-09-01

(1)、问题描述：给出2个序列，x是从1到m，y是从1到n，找出x和y的最长公共子序列？

x：A B C B D A B

y：B D C A B A

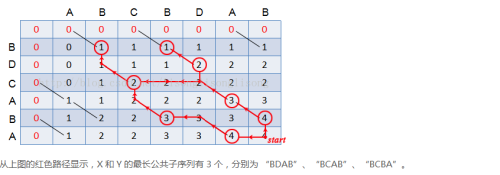
则：最长公共子序列长度为4，BDAB BCAB BCBA均为LCS(最长公共子序列)；

模型实现图：

(2)、问题解决

  代码实现了最长公共子序列的长度

#include<stdio.h>

#define N    10

int LCS(int *a, int count1, int *b, int count2);
int LCS(int *a, int count1, int *b, int count2){
    int table[N][N] = {0};
    int i;
    int j;

    for(i = 0; i < count1; i++){
        for(j = 0; j < count2; j++){
            if(a[i] == b[j]){
                table[i+1][j+1] = table[i][j]+1;
            }else{
                table[i+1][j+1] = table[i+1][j] > table[i][j+1] ? table[i+1][j] : table[i][j+1];
            }
        }
    }

    return table[count1][count2];
}

void main(void){
    int a[] = {1, 2, 3, 4, 5, 6};
    int b[] = {2, 3, 5, 6, 7};
    int count1 = sizeof(a)/sizeof(int);
    int count2 = sizeof(b)/sizeof(int);
    int number;

    number = LCS(a, count1, b, count2);
    printf("%d\n", number);
}

  结果截图

      

(3)、动态规划的特征：

  特征一(最优子结构的性质)：一个问题的最优解包含了子问题的最优解；

  特征二：重叠子问题，一个递归的过程包含很少的独立子问题被反复计算了多次；

  时间复杂度：O(m*n)；

 

本文出自 “wait0804” 博客，请务必保留此出处http://wait0804.blog.51cto.com/11586096/1899611