红黑树的删除

Posted 2020-11-07 Lune-Qiu

红黑树的删除共有12种情况，

设要删除的节点为Z:

1.Z为根  且没有孩子   直接删除，将根赋空

2.Z为根    有一个红孩子（由于第4条性质一定为红孩子） 将孩子颜色->黑，当做新的根，删除节点

3.Z红色   直接删除，判断Z为父亲的左孩子或右孩子 将其赋空  （此节点一定没有孩子，因为2个孩子的已经处理过，一个红孩子（两个红色节点不能相邻），一个黑孩子（到终端节点黑节点数相同））

4.Z为黑色   有一个红孩子   将红孩子->黑，Z的父与Z的子相连，删除Z

5.Z为黑色   没有孩子（由于要删除的是黑节点，整个过程通俗的理解就是想要借一个黑节点；当侄子为红节点则可以变为黑节点，然后借来一个黑节点）

　　5.1 兄弟为红（初始状态）

　　　　兄是父右，兄->黑，父->红 ，以父为支点左旋   更新兄

　　　　　　

　　　　

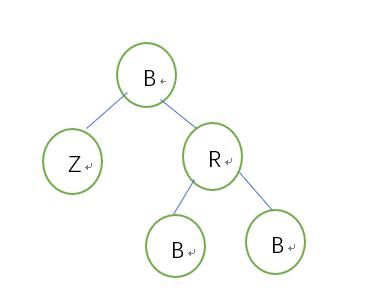
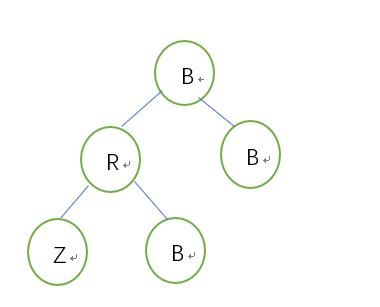
　　　　　　兄是父左，兄->黑，父->红，以父为支点右旋，更新兄

　　5.2兄弟为黑（初始状态或调整状态）

　　　　5.2.1左侄黑，右侄黑

　　　　　　5.2.1.1父黑：   兄->红，以父亲为当前节点向上调整    ，更新兄 （由于少了一个黑节点，则向上借黑节点）

　　　　　　　　初始状态：

　　　　　　　　　　　　 

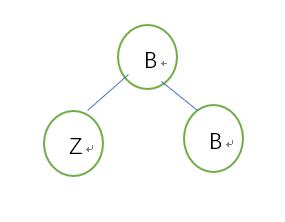
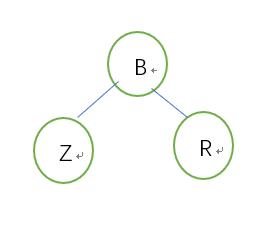
　　　　　　　　调整状态：

  　　　　　　　　　　　

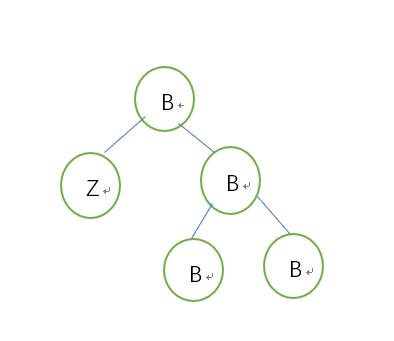
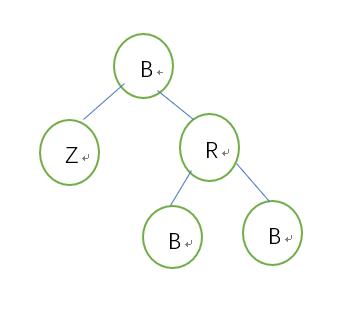
　　　　　　5.2.1.2父红：兄->红，父->黑，结束

　　　　　　　　初始状态：

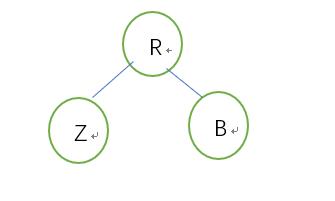
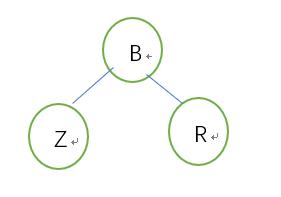　　　　　　　　　　删除Z即可

　　　　　　　　调整中：

　　　　　　　　　　

 

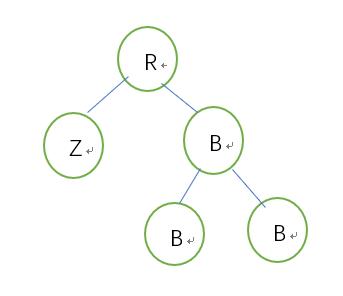
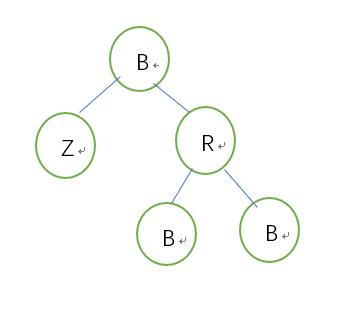
 　　　　5.2.2左侄子红，右侄子黑

　　　　　　5.2.2.1兄为父右：左侄子->黑，兄->红，以兄弟为支点右旋  ，更新兄

　　　　　　　　初始状态：

　　　　　　　　　　

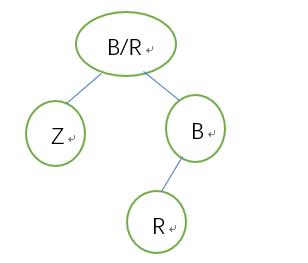
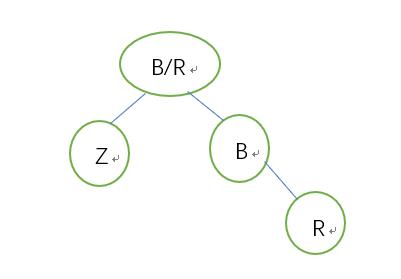
　　　　　　　　调整中：

　　　　　　　　　　

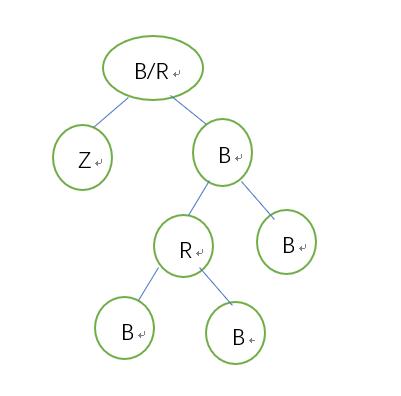
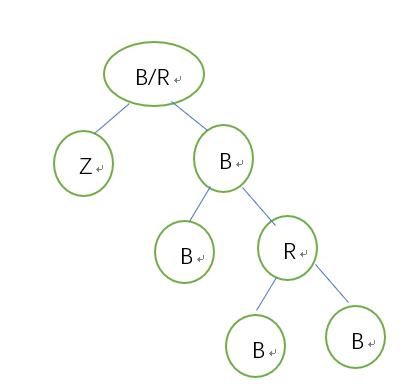
 　　　　　　5.2.2.2兄为父右：兄弟->父亲的颜色，父->黑，左侄->黑，以父亲为节点右旋  结束

　　　　5.2.3右侄红（右侄子红，左侄子黑；或者右侄子红）

　　　　　　5.2.3.1兄为父右：兄弟->父亲的颜色,父->黑，右侄->黑，以父亲为支点左旋  结束

　　　　　　　　初始状态：

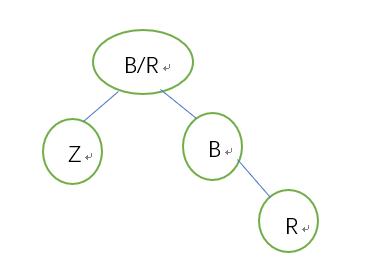
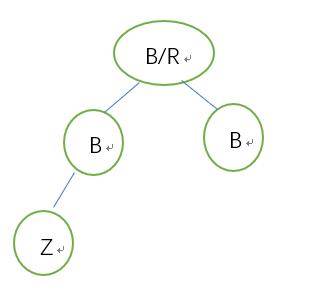　　　　　　　　　删除Z即可

　　　　　　　　调整中：

　　　　　　　　　

 

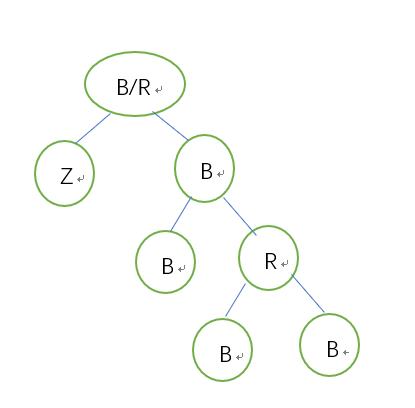
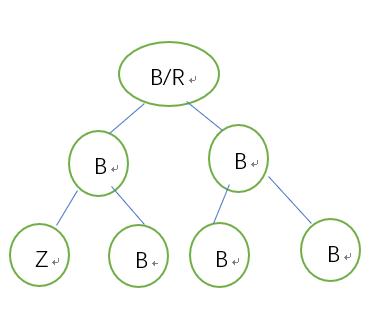
 　　　　　　5.2.3.2兄为父左：右侄->黑，兄->红，以兄弟为支点右旋 ，更新兄弟

 

 　　　　　　通过上图，可以看出，5.2.2.1状态的下一个状态是5.2.3.1

　　　　　　　　　　　　　　　　5.2.3.2状态点的下一个状态是5.2.2.2

代码：需要注意的就是：更新兄弟的时候，由于使用的假删除，要特别注意

RBT* Search(RBT* pRBT,int num)
{
    if(pRBT == NULL) return NULL;
    while(pRBT)
    {
        if(pRBT->val == num)
            return pRBT;
        else if(pRBT->val > num)
            pRBT = pRBT->pLeft;
        else
            pRBT = pRBT->pRight;
    }
    return NULL;
}
RBT* GetBrother(RBT* pRBT)
{
    if(pRBT == NULL) return NULL;
    if(pRBT == pRBT->pFather->pLeft)
        return pRBT->pFather->pRight;
    else
        return pRBT->pFather->pLeft;
}
void DelNode(RBT* pRBT,int num)
{
    if(pRBT == NULL) return ;
    RBT* pdel = Search(pRBT,num);//原始要删除的点
    RBT* ptmp = pdel;//真正要删除的点
    if(pdel == NULL) return;
    if(pdel->pLeft && pdel->pRight)
    {
        ptmp = pdel->pLeft;
        while(ptmp->pRight)
        {
            ptmp = ptmp->pRight;
        }
        pdel->val = ptmp->val;
    }
    if(ptmp == rbt)//为根
    {
        //没有孩子
        if(ptmp->pLeft == NULL && ptmp->pRight == NULL)
        {
            free(ptmp);
            ptmp = NULL;
            rbt = NULL;
            return;
        }
        //有一个孩子
        if(ptmp->pLeft != NULL || ptmp->pRight != NULL)
        {
            rbt = ptmp->pLeft ? ptmp->pLeft : ptmp->pRight;
            free(ptmp);
            ptmp = NULL;
            rbt->color = BLACK;
            rbt->pFather = NULL;
            return;
        }
    }


    //红色
    if(ptmp->color == RED)
    {
        if(ptmp->pFather->pLeft == ptmp)
            ptmp->pFather->pLeft = NULL;
        else
            ptmp->pFather->pRight = NULL;
        free(ptmp);
        ptmp = NULL;
        return;
    }
    if(ptmp->color == BLACK)//真正要删除节点为黑
    {
        //有一个红孩子
        if(ptmp->pLeft || ptmp->pRight)
        {
            if(ptmp == ptmp->pFather->pLeft)
            {
                ptmp->pFather->pLeft = ptmp->pLeft ? ptmp->pLeft : ptmp->pRight;
                ptmp->pFather->pLeft->pFather = ptmp->pFather;
                ptmp->pFather->pLeft->color = BLACK;
            }
            else
            {
                ptmp->pFather->pRight = ptmp->pLeft ? ptmp->pLeft : ptmp->pRight;
                ptmp->pFather->pRight->pFather = ptmp->pFather;
                ptmp->pFather->pRight->color = BLACK;
            }
            free(ptmp);
            ptmp = NULL;
            return;
        }
        //没有孩子
        if(ptmp->pLeft == NULL && ptmp->pRight == NULL)
        {
            RBT* pbrother = GetBrother(ptmp);
            RBT* pfather = ptmp->pFather;
　　　　　　　//假删除
            if(ptmp == pfather->pLeft)
                pfather->pLeft = NULL;
            else
                pfather->pRight = NULL;
            pdel = ptmp;
            while(1)
            {
                //兄弟红
                if(pbrother != NULL && pbrother->color == RED)
                {
                    pbrother->color = BLACK;
                    pbrother->pFather->color = RED;
                    if(pbrother == pbrother->pFather->pRight)
                    {
                        pbrother = pbrother->pLeft;//更新兄弟，为左侄子
                        LeftSpin(&ptmp->pFather);
                        continue;
                    }
                    if(pbrother == pbrother->pFather->pLeft)
                    {
                        pbrother = pbrother->pRight;//更新兄弟为右侄子
                        RightSpin(&ptmp->pFather);
                        continue;
                    }
                }
                //兄弟黑
                if(pbrother->color == BLACK)
                {
                    //两个侄子黑或者没有侄子
                    if((pbrother->pLeft && pbrother->pLeft->color == BLACK &&
                        pbrother->pRight && pbrother->pRight->color == BLACK)||
                            (pbrother->pLeft == NULL && pbrother->pRight == NULL))
                    {
                        if(pbrother->pFather->color == RED)
                        {
                            pbrother->pFather->color = BLACK;
                            pbrother->color = RED;
                            break;
                        }
                        if(pbrother->pFather->color == BLACK)
                        {
                            pbrother->color = RED;
                            ptmp = ptmp->pFather;
                            if(ptmp->pFather == NULL)
                                break;
                            pbrother = GetBrother(ptmp);
                            continue;
                        }
                    }
                    //左侄子为红，右侄子为黑
                    if(pbrother->pLeft && pbrother->pLeft->color == RED &&
                       (pbrother->pRight == NULL || pbrother->pRight->color == BLACK) )
                    {
                        //兄为父右
                        if(pbrother == pbrother->pFather->pRight)
                        {
                            pbrother->pLeft->color = BLACK;
                            pbrother->color = RED;
                            RightSpin(&pbrother);
                            pbrother = pbrother->pFather;//由于要以兄弟节点右旋，所以旋转完再更新
                            continue;
                        }
                        //兄为父左
                        if(pbrother == pbrother->pFather->pLeft)
                        {
                            pbrother->color = pbrother->pFather->color;
                            pbrother->pLeft->color = BLACK;
                            pbrother->pFather->color = BLACK;
                            RightSpin(&ptmp->pFather);
                            break;
                        }
                    }
                    //右侄子为红
                    if(pbrother->pRight && pbrother->pRight->color == RED)
                    {
                        //兄为父右
                        if(pbrother == pbrother->pFather->pRight)
                        {
                            pbrother->pRight->color = BLACK;
                            pbrother->color = pbrother->pFather->color;
                            pbrother->pFather->color = BLACK;
                            LeftSpin(&ptmp->pFather);
                            break;
                        }
                        //兄为父左
                        if(pbrother == pbrother->pFather->pLeft)
                        {
                            pbrother->pRight->color = BLACK;
                            pbrother->color = RED;
                            LeftSpin(&pbrother);
                            pbrother = pbrother->pFather;//兄弟更新
                            continue;
                        }
                    }
                }
            }
        }
    }
    free(pdel);
    pdel = NULL;
}

　　　　这篇博客是有史以来写的最认真的一个了，希望下次看的时候一下就能看懂，也希望能对看到这篇博客的人有一些帮助~