ConcurrentHashMap(JDK1.8)中红黑树的实现
Posted 顧棟
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ConcurrentHashMap(JDK1.8)中红黑树的实现相关的知识，希望对你有一定的参考价值。
ConcurrentHashMap(JDK1.8)中红黑树的实现
文章目录
本文只介绍红黑树的实现 不对并发容器ConcurrentHashMap进行介绍。
红黑树的理论和基础试下可以阅读红黑树与JAVA实现
红黑树特性
- 每个结点的或是黑色或是红色
- 根结点是黑色
- 每个叶子结点都是黑色（NIL）
- 如果一个结点是红色，那么它的子结点必须是黑色
- 对任意一结点，该结点到其叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点
ConcurrentHashMap数据结构示意图
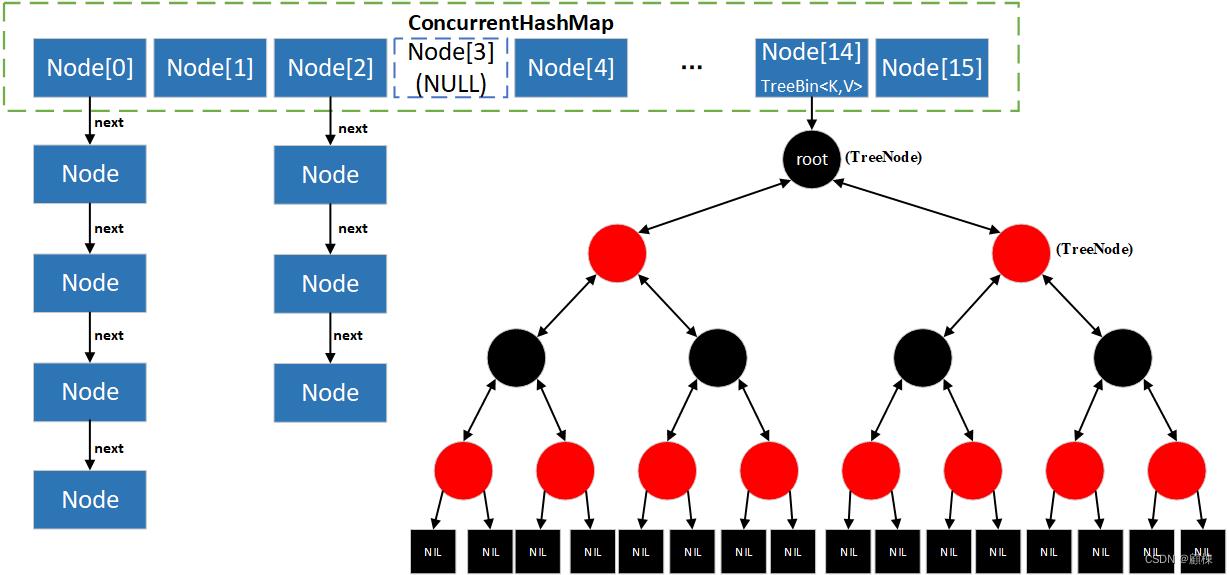
代码实现分析
结点组成
Node<K,V>
// key的hash值
final int hash;
// 关键字
final K key;
// 存储值
volatile V val;
// 下一个结点
volatile Node<K,V> next;
TreeNode<K,V>
作为红黑树结构的存储结构，比一般红黑树存储结构出来的next和prev，可以将这些结点变成双向的链表结构，是为了方便从链表变为红黑树，在从红黑树变成链表。在ConcurrentHashMap中，链表与红黑树的转变是依据链表中的结点数量，默认变成红黑树的链表结点个数需要大于8。
| hash | key | val | next | prev | parent | left | right | red |
|---|
static final class TreeNode<K,V> extends Node<K,V>
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next,
TreeNode<K,V> parent)
super(hash, key, val, next);
this.parent = parent;
Node<K,V> find(int h, Object k)
return findTreeNode(h, k, null);
/**
* Returns the TreeNode (or null if not found) for the given key
* starting at given root.
*/
final TreeNode<K,V> findTreeNode(int h, Object k, Class<?> kc)
if (k != null)
TreeNode<K,V> p = this;
do
int ph, dir; K pk; TreeNode<K,V> q;
TreeNode<K,V> pl = p.left, pr = p.right;
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
else if ((pk = p.key) == k || (pk != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.findTreeNode(h, k, kc)) != null)
return q;
else
p = pl;
while (p != null);
return null;
TreeBin<K,V>
继承Node，树标记结构，表明该结点背后有一棵红黑树。在新增结点和删除结点的时候，为了并发的安全都需要会进行锁的竞争。root和first不应该是同一个结点。
TreeNode<K,V> root; // 树根结点
volatile TreeNode<K,V> first; // 首结点
volatile Thread waiter; // 等待的线程
volatile int lockState; // 结点锁的情况
主要方法
构造函数
从给定的b结点开始，遍历整个链表，构建红黑树。
TreeBin(TreeNode<K,V> b)
super(TREEBIN, null, null, null);
// 参数b的值为首结点
this.first = b;
// 根结点
TreeNode<K,V> r = null;
// 从首结点开始遍历链表
for (TreeNode<K,V> x = b, next; x != null; x = next)
// 获取下一个结点
next = (TreeNode<K,V>)x.next;
// 初始化x的左右子结点 置null
x.left = x.right = null;
// 设置根结点，颜色为黑色
if (r == null)
x.parent = null;
x.red = false;
r = x;
else
// 结点的关键字
K k = x.key;
// 结点的hash
int h = x.hash;
Class<?> kc = null;
// 遍历以r为根的树
for (TreeNode<K,V> p = r;;)
int dir, ph;
K pk = p.key;
// dir-1 左子 dir1 右子
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
// 当 hashCodes 相等且不可比较时，用于排序插入的打破平局实用程序。 我们不需要总排序，只需要一致的插入规则来保持重新平衡之间的等价性。 简化了比较平局的处理逻辑。
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
// p作为x的双亲结点，确认x是双亲结点p的左子还是右子
if ((p = (dir <= 0) ? p.left : p.right) == null)
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 保证红黑树的性质
r = balanceInsertion(r, x);
break;
this.root = r;
assert checkInvariants(root);
新增节点修复红黑树方法
balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x)
root为根，x为新增的那个结点，新增的结点都为红色。
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x)
// 先将x变为红结点
x.red = true;
// x的双亲结点xp
// x的祖父结点xpp
// x的祖父结点xpp的左子结点xppl
// x的祖父结点xpp的右子结点xppr
for (TreeNode<K,V> xp, xpp, xppl, xppr;;)
// 若x的父结点为空，则将节点置为黑，直接返回x即为根结点退出for。
if ((xp = x.parent) == null)
x.red = false;
return x;
// 此时父节点不为null，若父节点是黑色的，那么不要调整，直接返回
// 若当前结点的祖父节点为空（说明父节点是根结点），直接返回根结点。
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 目前父节点是红色的 若父节点是祖父的左子结点
if (xp == (xppl = xpp.left))
// 叔叔结点是红色
// 将双亲节点和叔叔结点变黑，祖父变红
// x指向祖父结点
if ((xppr = xpp.right) != null && xppr.red)
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
// 以下叔叔结点是黑色
else
// 当前结点是双亲结点的右子
if (x == xp.right)
//当前x指向双亲结点 ，以双亲节点为根进行左旋
root = rotateLeft(root, x = xp);
// 取x的祖父结点
xpp = (xp = x.parent) == null ? null : xp.parent;
if (xp != null)
// 当前结点是双亲结点的左子
// 双亲结点变黑
xp.red = false;
// 若还有祖父结点，将祖父结点变红，以祖父结点为支点进行右旋
if (xpp != null)
xpp.red = true;
root = rotateRight(root, xpp);
// 目前父节点是红色的 若父节点是祖父的右子结点
else
// 叔叔结点是红色
// 将双亲节点和叔叔结点变黑，祖父变红
// x指向祖父结点
if (xppl != null && xppl.red)
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
// 以下叔叔结点是黑色
else
// 当前结点是双亲结点的左子
if (x == xp.left)
//当前x指向双亲结点 ，以双亲节点为根进行右旋
root = rotateRight(root, x = xp);
// 取x的祖父结点
xpp = (xp = x.parent) == null ? null : xp.parent;
if (xp != null)
// 当前结点是双亲结点的右子
// 双亲结点变黑
xp.red = false;
// 若还有祖父结点，将祖父结点变红，以祖父结点为支点进行左旋
if (xpp != null)
xpp.red = true;
root = rotateLeft(root, xpp);
左旋方法
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p)
// r右子结点 pp是p的双亲结点 rl是r的左子结点
TreeNode<K,V> r, pp, rl;
// 若p是空 或者p没有右子 不进行左旋
if (p != null && (r = p.right) != null)
// 若r存在左子，则变为p的右子
if ((rl = p.right = r.left) != null)
rl.parent = p;
// 若p的双亲结点为空（p是当前的根结点），则r变为根结点，r颜色变黑
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
// 目前p的双亲结点不为空，若p是双亲结点的左子，将r变为双亲结点的左子
else if (pp.left == p)
pp.left = r;
// 若p是双亲结点的右子，将r变为双亲结点的右子
else
pp.right = r;
// r的左子变为p，p的双亲结点变为r
r.left = p;
p.parent = r;
// 旋转结束，返回实际根结点
return root;
右旋方法
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p)
// l是左子结点 pp是p的双亲结点 lr是l的右子结点
TreeNode<K,V> l, pp, lr;
// 若p是空 或者p没有左子 不进行右旋
if (p != null && (l = p.left) != null)
// 若l存在右子，则p变为l的左子
if ((lr = p.left = l.right) != null)
lr.parent = p;
// 若p的双亲结点为空（p是当前的根结点），则l变为根结点，l颜色变黑
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
// 目前p的双亲结点不为空，若p是双亲结点的右子，将l变为双亲结点的右子
else if (pp.right == p)
pp.right = l;
// 若p是双亲结点的左子，将r变为双亲结点的左子
else
pp.left = l;
// l的右子变为p，p的双亲结点变为r
l.right = p;
p.parent = l;
// 旋转结束，返回实际根结点
return root;
红黑树特性检查方法
static <K,V> boolean checkInvariants(TreeNode<K,V> t)
// t 从根开始遍历的结点
// tp 为t的双亲结点
// tl 为t的左子
// tr 为t的右子
// tb 为t的前驱
// tn 为t的后继
TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right,
tb = t.prev, tn = (TreeNode<K,V>)t.next;
// 前驱的后继不是本身--链表结点关系出现混乱
if (tb != null && tb.next != t)
return false;
// 后继的前驱不是本身--链表结点关系出现混乱
if (tn != null && tn.prev != t)
return false;
// t 不是双亲结点的左右子--树结点关系出现混乱
if (tp != null && t != tp.left && t != tp.right)
return false;
// t的左子的双亲结点不是t，或者左子的hash值大于t的hash--树结点关系出现混乱
if (tl != null && (tl.parent != t || tl.hash > t.hash))
return false;
// t的右子的双亲结点不是t，或者右子的hash值小于t的hash--树结点关系出现混乱
if (tr != null && (tr.parent != t || tr.hash < t.hash))
return false;
// t是红色 且左右子也是红色 if ((t.red && tl != null && tl.red)||(t.red && tr != null && tr.red))？？？
// 这个是说明结点是红色，其左右子不可以同时为红色，不应该是不论哪个子结点为红色也不可以吗？
if (t.red && tl != null && tl.red && tr != null && trJDK1.8中的ConcurrentHashMap
ConcurrentHashMap 源码详细分析(JDK1.8)
ConcurrentHashMap(JDK1.8)中红黑树的实现
JUC系列并发容器之ConcurrentHashMap(JDK1.8版)