最大堆和最小堆

Posted 2020-11-03 outthinker

参考：https://blog.csdn.net/guoweimelon/article/details/50904346

一、堆树的定义

堆树的定义如下：

（1）堆树是一颗完全二叉树；

（2）堆树中某个节点的值总是不大于或不小于其孩子节点的值；

（3）堆树中每个节点的子树都是堆树。

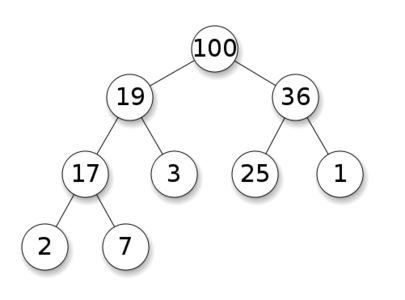
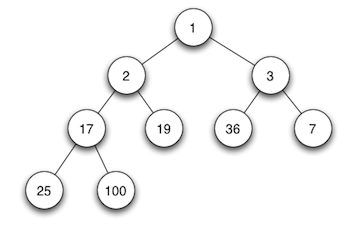
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如下图所示，左边为最大堆，右边为最小堆。

二、堆树的操作

以最大堆为例进行讲解，最小堆同理。

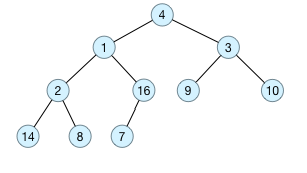
原始数据为a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}，采用顺序存储方式，对应的完全二叉树如下图所示：

（1）构造最大堆

在构造堆的基本思想就是：首先将每个叶子节点视为一个堆，再将每个叶子节点与其父节点一起构造成一个包含更多节点的对。

所以，在构造堆的时候，首先需要找到最后一个节点的父节点，从这个节点开始构造最大堆；直到该节点前面所有分支节点都处理完毕，这样最大堆就构造完毕了。

假设树的节点个数为n，以1为下标开始编号，直到n结束。对于节点i，其父节点为i/2；左孩子节点为i*2，右孩子节点为i*2+1。最后一个节点的下标为n，其父节点的下标为n/2。

 

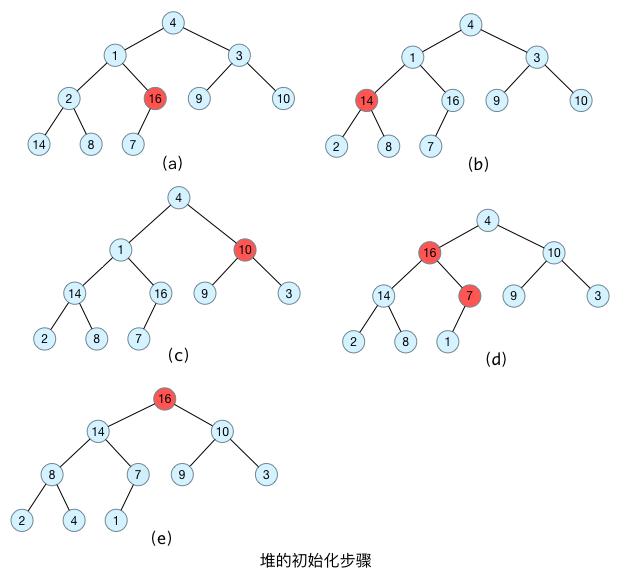
如下图所示，最后一个节点为7，其父节点为16，从16这个节点开始构造最大堆；构造完毕之后，转移到下一个父节点2，直到所有父节点都构造完毕。

注意：上面构造最大堆的时候，从底而上，一层一层地不断基于父节点构造最大堆，直至到达根节点完成整个最大堆的构造；

代码如下：

//最大堆
//=======================================================================

#include <iostream>

using namespace std;

struct MaxHeap
{
    int *heap;  //数据元素的存放空间，下标从1开始存放元素，下标0存放临时数据
    int HeapSize;  //数据元素的个数
    int MaxSize;  //存放数据元素空间的大小
};

//初始化最大堆
void MaxHeapint(MaxHeap &H)  
{
    for (int i = H.HeapSize / 2; i > 0; i--)
    {
        H.heap[0] = H.heap[i];
        int son = i * 2;
        while (son <= H.HeapSize)
        {
            if (son < H.HeapSize && H.heap[son] < H.heap[son + 1])
                son++;
            if (H.heap[son] < H.heap[0])
                break;
            else
            {
                H.heap[son / 2] = H.heap[son];
                son *= 2;
            }
        }
        H.heap[son / 2] = H.heap[0];
    }
}

//最大堆中插入节点
//思想：先在堆的最后添加一个节点，然后沿着堆树上升。
void MaxHeapInsert(MaxHeap &H, int x)
{
    if (H.HeapSize == H.MaxSize)
        return;
    int i = ++H.HeapSize;
    while (i != 1 && x > H.heap[i / 2])
    {
        H.heap[i] = H.heap[i / 2];
        i = i / 2;
    }
    H.heap[i] = x;
}

//最大堆堆顶节点删除
//思想：将堆树的最后的节点提到根结点，然后删除最大值，然后再把新的根节点放到合适的位置。
void MaxHeapDelete(MaxHeap &H , int &top)
{
    int x;
    if (H.HeapSize == 0)
        return;
    top = H.heap[1];
    H.heap[0] = H.heap[H.HeapSize--];
    int i = 1, son = i * 2;
    while (son <= H.HeapSize)
    {
        if (son < H.HeapSize && H.heap[son] < H.heap[son + 1])
            son++;
        if (H.heap[0] >= H.heap[son])
            break;
        H.heap[i] = H.heap[son];
        i = son;
        son = son * 2;
    }
    H.heap[i] = H.heap[0];
    return;
}

int main(void)
{
    int top;
    int &top_1 = top;
    MaxHeap H;
    cout << "请输入数据的size: " << endl;
    cin >> H.HeapSize;
    H.heap = new int(H.HeapSize + 1);
    cout << "请按照完全二叉树输入数据：" << endl;
    for (int i = 0; i <= H.HeapSize; i++)
    {
        cin >> H.heap[i];  //我们这里默认H.heap[0]为临时数据，设为0
    }
    
    MaxHeapint(H);  //将二叉树转换为最大堆
    MaxHeapInsert(H, 3);
    MaxHeapDelete(H, top);

    for (int i = 1; i <= H.HeapSize; i++)
    {
        cout << H.heap[i] << "  ";
    }
    cout << endl << top;
    system("pause");
}