机器学习周志华 读书笔记 第三章 线性模型

Posted 2020-11-01 Barry

1. 基本形式

f(æ) = ω1 X1 + ω2 X2 十...+ωdXd + b ,

2.线性回归

均方误差有非常好的几何意义--它对应了常用的欧几里得距离或简称"欧

氏距离" (Euclidean distance). 基于均方误差最小化来进行模型求解的方法称为"最小二乘法" (least squ町e method). 在线性回归中，最小A乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小.

 

 3.对数几率回归

 

 

 

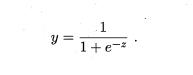
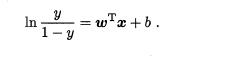
若将y视为样本x 作为正例的可能性，则1-y 是其反例可能性，两者的比值

 

 

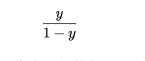
称为"几率" (odds) ，反映了m 作为正例的相对可能性.对几率取对数则得到

"对数几率" (log odds ，亦称logit)

 

 

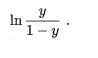
   因此，其对应的模型称为"对数几率回归" (logistic regression)特别需注意到，虽然它的名字是"回归"，但实际却是一种分类学习方法.这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先假设数据分布?这样就避免了假设分布不准确所带来的问题;它不是仅预测出"类别"，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用;此外，对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解.

 

4.对数几率回归训练方式？

    我们知道，对数几率回归函数的输出值是一个概率。那么一个对率回归模型越好，意味着当输入模型的样本为正例时，模型的输出值越大（越接1）当输入模型的样本为反例时，模型的输出值越小（越接近0）。因此我们可以构建一个函数

 

 

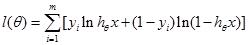
上式中hθx是对率模型的输出值，yi是样本的真实标记，当样本为正例时y取1，为反例时y取0。这整一个函数的含义就是把每个样本属于其真实标记的概率加起来。若我们使l(θ)最大，那就可以找到一组θ使得每个样本属于其真实标记的概率最大，亦即使得正例的函数值尽可能接近1，反例的函数值尽可能接近0。如此我们就得到了一个优秀的对数几率回归模型。

 

5.线性判别分析

线性判别分析(Linear Discriminant Analysis，简称LDA) 是一种经典的线性学习方法.

LDA 的思想非常朴素: 给定训练样例集, 设法将样例投影到一条直线上，

使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样

本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别. 图3.3 给出了一个二维示意图.

 

 

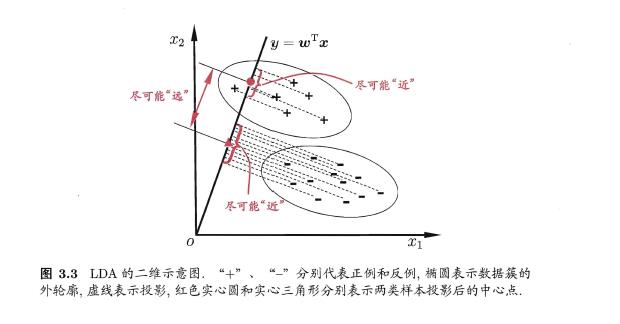
1. 多分类学习

解决思路一般有一对一，一对多，和多对多三种。

一对一策略：举个例子，现在有A、B、C、D四个种类，要确定某个样本属于四类中的哪一类。那么我们可以事先训练好六个二分类的分类器——A/B、A/C、A/D、B/C、B/D、C/D。然后把要确定类别的样本分别放入这六个分类器。假设分类结果分别是A、A、A、B、D、C。可以知道六个分类器中有三个认为这个样本术语A，认为是B、C、D的各有一个。所以我们可以认为这个样本就是术语A类的。

一对多策略：举个例子，现在有A、B、C、D四个种类，要确定某个样本属于四类中的哪一类。那么我们可以事先训练好四个二分类的分类器——A/BCD、B/ACD、C/ABD、D/ABC,分类器输出的是一个函数值。然后把要确定类别的样本分别放入这四个分类器。假设四个分类器的结果分别是“属于A的概率是0.9”，“属于B的概率是0.8”、“属于C的概率是0.7”、“属于B的概率是0.6”。那我们可以认为这个样本是属于A。

多对多策略：每次将若干个类作为正类，若干个其他类作为反类。其中需要这种策略需要特殊的设计，不能随意取。常用的技术：纠错输出码。工作步骤分为：

• 编码：对N个类别做M次划分，每次划分将一部分类别作为正类，一部分划分为反类，从而形成一个二分类训练集；这样一共产生M个训练集，可以训练出M个分类器。
• 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码，将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别最为最终预测结果。

 

 

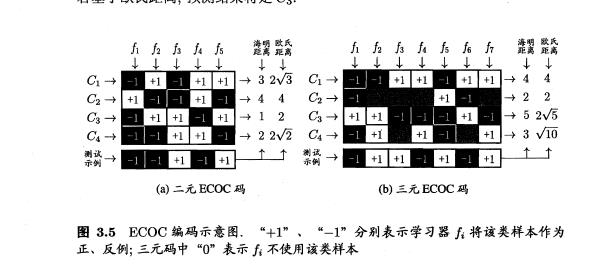
以原书的例子做一个详细的演示：
假如现在有一个训练数据集，可以分四个类——C1, C2, C3, C4
再具体一点可以想像为——西瓜可以分为一等瓜、二等瓜、三等瓜、四等瓜，要训练一个分类系统，使之能判断一个西瓜的等级。

我们对训练数据集做五次划分

• 第一次，标记C2为正例，其他为反例，训练出一个二分类的分类器f1
• 第二次，标记C1、C3为正例，其他为反例，训练出一个二分类的分类器f2
• 第三次，标记C3、C4为正例，其他为反例，训练出一个二分类的分类器f3
• 第四次，标记C1、C2、C4为正例，其他为反例，训练出一个二分类的分类器f4
• 第五次，标记C1、C4为正例，其他为反例，训练出一个二分类的分类器f5

根据这五次划分的过程，每一个类都获得了一个编码（向量）：

• C1：（-1，1，-1，1，1）
• C2：（1，-1，-1，1，-1）
• C3：（-1，1，1，-1，1）
• C4：（-1，-1，1，1，-1）

若现在有一个测试样本，五个分类器对应的累计结果为
f1：反， f2：反， f3：正， f4：反， f5：正
即该测试样本对应的编码/向量为（-1，-1，1，-1，1）
那么分别计算这个测试样本的编码与四个类别的编码的向量距离，可以使用欧氏距离，算的与C3类的距离是最小的。因此判定该测试样本属于C3类。

 

补充

Gradient Descent for Multiple Variables

The gradient descent equation itself is generally the same form; we just have to repeat it for our \'n\' f

eatures:

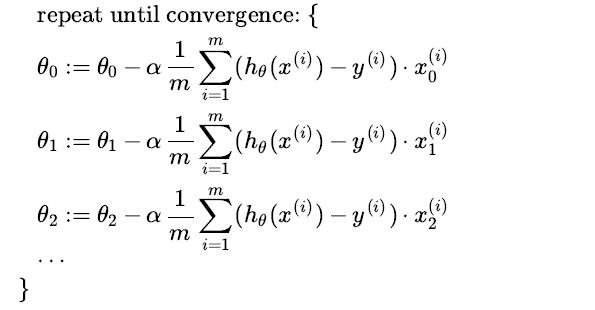
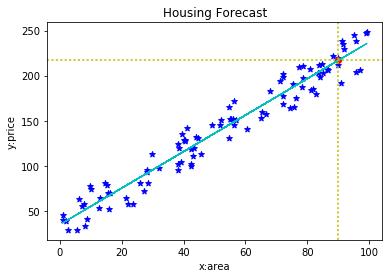
 Programming Example ---simple linear regression predicting house price

# -*- coding: utf-8 -*-
"""
Created on Thu Apr 26 10:15:38 2018

_author: wangchen
_email: [e-mail]
_Anhui Jianzhu University
"""

#!/usr/bin/env python
# encoding: utf-8


# Required Packages
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model


def get_data():
    """
    生成随机的线性数据集
    :return: 
    """
    x = 100 * np.random.rand(100, 1).astype(np.float32)
    y = 2 * x + 10  # 直线
    # y = 7 * x ** 5 + 3 * x + 10  # 曲线
    y += 50 * np.random.rand(100, 1).astype(np.float32)
    return x, y


# Function for Fitting our data to Linear model
def linear_model_main(X_parameters, Y_parameters, predict_value):
    # Create linear regression object
    regr = linear_model.LinearRegression()
    regr.fit(X_parameters, Y_parameters)
    predict_outcome = regr.predict(predict_value)

    predictions = {}
    predictions[\'intercept\'] = regr.intercept_
    predictions[\'coefficient\'] = regr.coef_
    predictions[\'predicted_value\'] = predict_outcome
    return predictions


# Function to show the resutls of linear fit model
def show_linear_line(X_parameters, Y_parameters, predictvalue):
    # Create linear regression object
    regr = linear_model.LinearRegression()
    regr.fit(X_parameters, Y_parameters)

    fig = plt.figure()
    ax1 = fig.add_subplot(111)
    # 设置标题
    ax1.set_title(\'Housing Forecast\')

    ax1.scatter(X_parameters, Y_parameters, color=\'blue\', marker=\'*\')
    ax1.plot(X_parameters, regr.predict(X_parameters), color=\'c\', linewidth=1)

    # 画点
    ax1.scatter(predictvalue, regr.predict(predictvalue), color=\'red\')

    # 画水平虚线
    plt.axvline(x=predictvalue, ls=\'dotted\', color=\'y\')
    plt.axhline(y=regr.predict(predictvalue), ls=\'dotted\', color=\'y\')

    plt.xlabel(\'x:area\')
    plt.ylabel(\'y:price\')

    plt.show()


if __name__ == "__main__":
    X, Y = get_data()
    predictvalue = 90  # 面积
    result = linear_model_main(X, Y, predictvalue)

    print("Intercept value ", result[\'intercept\'])
    print("coefficient", result[\'coefficient\'])
    print("Predicted value: ", result[\'predicted_value\'])
    print("面积 %d 的价格预测为 %d" % (predictvalue, result[\'predicted_value\']))

    show_linear_line(X, Y, predictvalue)

Output  

Intercept value [ 34.93412135]
coefficient [[ 2.02093196]]
Predicted value: [[ 216.81799767]]
面积 90 的价格预测为 216