周志华 机器学习初步 线性模型

Posted 2022-12-21 临风而眠

周志华 《机器学习初步》 线性模型

还未更新完，会持续更新

文章目录

• 周志华 《机器学习初步》 线性模型
• 一.线性回归
• • 1.线性模型
  • • 线性模型的特点和重要性
    • 线性模型的基本形式
  • 2.线性回归
  • • 离散属性的处理
    • 性能度量：均方误差/平方损失（square loss）
• 二.最小二乘解
• 参考资料

一.线性回归

1.线性模型

线性模型的特点和重要性

• 线性模型的重要性

  • 人在考虑问题时，通常不是直接去思考一些非线性的问题。
  • 而考虑线性的问题，我们马上会有一个几何的直观的印象。基于这种几何直观的印象，我们可能能够从直观上得到一些解决方案，之后在线性模型的基础上可能得到针对非常复杂的非线性问题的解决方案

  

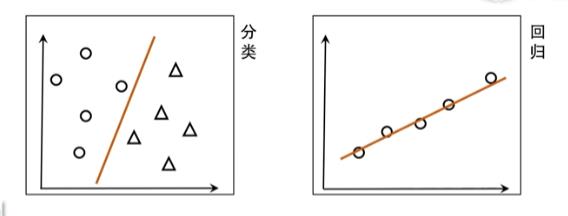
  • 比如要用线性模型去做分类和回归
    • 分类，找一条线把两类点分开
    • 回归，找一条线把点串起来

• 线性模型的特点：简单、基本、可理解性(understandability)/可解释性(comprehensibility)好

  • 线性模型形式简单、易于建模, 但却蕴涵着机器学习中一些重要的基本思想, 许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上 通过引入层级结构或高维映射而得
  • 此外, 由于 $\mathbf{w}$ 直观表达了各属性在预测中的重要性(权重), 因此线性模型有很好的可解释性
    • 例如若在西瓜 问题中学得 “ $f_{好瓜}(\mathbf{x})=0.2\cdot x_{\text{色泽 }}+0.5\cdot x_{\text{根蒂 }}+0.3\cdot x_{\text{敲声 }}+1$ ”, 则意味着可通过综合考虑色泽、根蒂和敲声来判断瓜好不好, 其中根蒂最要紧, 而敲声比色泽更重要.

线性模型的基本形式

• 给定由 d 个属性描述的示例 $\mathbf{x}=\left(x_1;x_2;\dots ;x_d\right)$, 其中 $x_i$ 是 $\mathbf{x}$ 在第 i 个属性上的取值, 线性模型(linear model)试图学得一个通过属性的线性组合来进行 预测的函数, 即
  $$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d+b,$$

• 一般用向量形式写成$f(\mathbf{x})={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b,$其中 $\mathbf{w}=\left(w_1;w_2;\dots ;w_d\right)$.

• $\mathbf{w}$ 和 $b$ 学得之后, 模型就得以确定.

2.线性回归

感觉老师这里用的“学得”这个词很好，之前在别的教程暂时没有看到这种表述哈哈，机器学习，“学得”

​ 给定数据集 $D=\left({\mathbf{x}}_1,y_1\right),\left({\mathbf{x}}_2,y_2\right),\dots ,\left({\mathbf{x}}_m,y_m\right),其中{\mathbf{x}}_i=(x_{i1};x_{i2};\dots ;x_{id}),y_i\in \mathbb{R}.$ “线性回归” (linear regression) 试图学得一个线性模型以尽可能准确地预测实值输出标记

• 线性回归试图学得
  $$f\left(x_i\right)=w{x}_i+b\text{ 使得 }f\left(x_i\right)\simeq y_i$$
  我们要找到这么一个线性方程，使得 f(x) 等于y，理想情况是完全相等。但由于有 overfitting 的存在，完全相等未必是好的，所以我们找一个约等于关系也是正确的。但是为了简化，把约等于符号写成等于也可以。

离散属性的处理

• 线性回归擅长的处理数值属性

  • 例如若在西瓜问题中学得 “ $f_{好瓜}(\mathbf{x})=0.2\cdot x_{\text{色泽 }}+0.5\cdot x_{\text{根蒂 }}+0.3\cdot x_{\text{敲声 }}+1$ ”,

    • x色泽如果是青绿、乌黑这种，x敲声是浑浊、清脆，这没法做加法，所以我们要把先把这些离散属性转换成数值。

  • 离散属性的处理

    先考虑一种最简单的情形: 输入属性的数目只有一个，为便于讨论, 此时我们忽略关于属性的下标, 即 $D={\left(x_i,y_i\right)}_{i=1}^m$, 其中 $x_i\in \mathbb{R}.$

    • 若有 “序” (order), 则连续化;
      • 对离散属性, 若属性值间存在 “序” (order) 关系, 可通过连续化将其转化为连续值, 例如二值属性 “身高” 的取值 “高” “矮” 可转化为 1.0,0.0, 三值属性 “高度” 的取值 “高” “中” “低” 可转化为 1.0,0.5,0.0;
      • 西瓜的颜色，青绿色，乌黑色，浅白色，我们分别赋予1，0.5，0？我们没法随意定序，这时候我们就不能把它简单的把当做1， 0 这样来处理。因为在具体算法的求解过程中，很可能会把 1 和 0 当成了数值关系。若将无序属性连续化, 则会不恰当地引入序关系， 对后续处理如距离计算等造成误导。
    • 否则, 转化为 k 维向量
      • 若属性值间不存在序关 系, 假定有 k 个属性值, 则通常转化为 k 维向量, 例如属性 “瓜类” 的取值 “西瓜” “南瓜” “黄瓜” 可转化为 (0,0,1),(0,1,0),(1,0,0).
      • 比如还是上面说的西瓜的颜色，青绿色，乌黑色，浅白色，我们可以分别是 (0,0,1),(0,1,0),(1,0,0).

性能度量：均方误差/平方损失（square loss）

• 我们怎么样去找一个线性回归的解决方案？（如何确定 w 和 b ）

  • 显然, 关键在于如何衡量 f(x) 与 y 之间的差别

  • 均方误差是回归任务中最常用的性能度量, 因此我们可试图让均方误差最小化, 即

    $w^{\ast },b^{\ast }$ 表示 w 和 b 的解.

    ( w ∗ , b ∗ ) = arg ⁡ min ⁡ ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2

    以上是关于周志华 机器学习初步 线性模型的主要内容，如果未能解决你的问题，请参考以下文章

    周志华 《机器学习初步》 绪论

    周志华老师的机器学习第五页中，若色泽，根蒂和敲声分别有3,2,2种可能

    机器学习笔记#1 线性回归

    机器学习周志华 读书笔记 第三章 线性模型

    周志华机器学习--模型评估与选择

    《机器学习》周志华 习题答案3.5