题目
lxhgww最近接到了一个生成字符串的任务，任务需要他把n个1和m个0组成字符串，但是任务还要求在组成的字符串中，在任意的前k个字符中，1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个，聪明的程序员们，你们能帮助他吗？
输入格式
输入数据是一行，包括2个数字n和m
输出格式
输出数据是一行，包括1个数字，表示满足要求的字符串数目，这个数可能会很大，只需输出这个数除以20100403的余数
输入样例
2 2
输出样例
2
提示
【数据范围】
对于30%的数据，保证1<=m<=n<=1000
对于100%的数据，保证1<=m<=n<=1000000
题解
比较一般的卡特兰数？
我们将问题转化为在一个二维平面上从\\((0,0)\\)到\\((n + m,n - m)\\)，每次可以走向量\\((1,1)\\)或\\((1,-1)\\)，不能跨越\\(y = 0\\)的直线，有多少种方案
显然总方案
\\[C_{n + m}^{m}
\\]
我们只考虑不合法方案即可
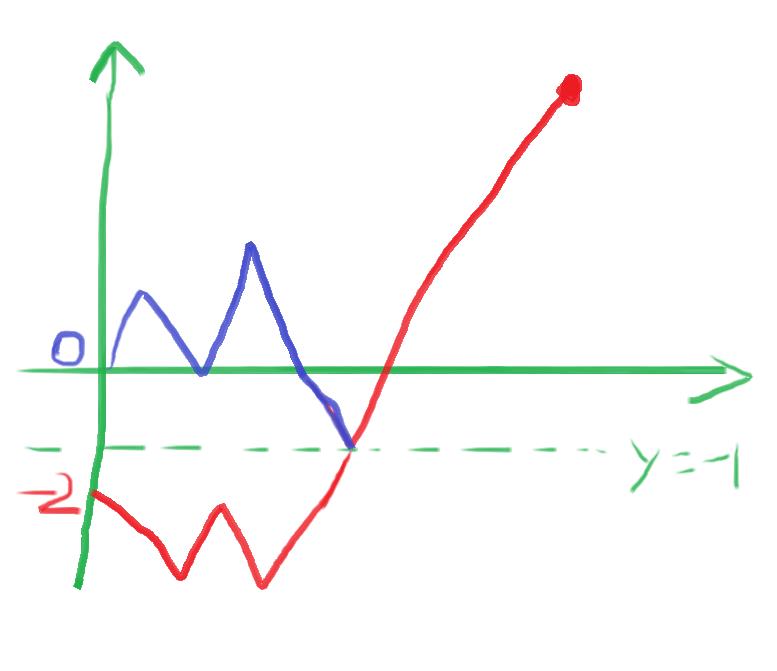
如图
所有不合法的方案一定会触及\\(y=-1\\)
我们将之前的曲线翻转，就可以转化为从\\((0,-2)\\)出发，其中操作数分别为\\(n+1\\)，\\(m-1\\)的方案数
即为
\\[C_{n + m}^{m - 1}
\\]
最后答案为:
\\[C_{n + m}^{m} - C_{n + m}^{m - 1}
\\]
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<\' \'; puts("");
using namespace std;
const int maxn = 2000005,maxm = 100005,INF = 1000000000,P = 20100403;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == \'-\') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
int fac[maxn],inv[maxn],fv[maxn];
void init(int E){
fac[0] = 1;
REP(i,E) fac[i] = 1ll * fac[i - 1] * i % P;
inv[0] = inv[1] = 1;
for (int i = 2; i <= E; i++) inv[i] = 1ll * (P - P / i) * inv[P % i] % P;
fv[0] = 1;
REP(i,E) fv[i] = 1ll * fv[i - 1] * inv[i] % P;
}
int C(int n,int m){
if (m > n) return 0;
return 1ll * fac[n] * fv[m] % P * fv[n - m] % P;
}
int main(){
int n = read(),m = read();
init(n + m);
printf("%d\\n",((C(n + m,m) - C(n + m,m - 1)) % P + P) % P);
return 0;
}