数学奥林匹克问题解答：平面几何-3

Posted 2020-07-10 赵胤数学课

已知：等腰梯形 $ABCD$ 中, $AD\\parallel BC$, 在 $AB$ 外作正方形 $ABPQ$, 在 $CD$ 外作正方形 $CDRS$, $QR$ 交 $AD$ 于 $E$, $PS$ 交 $BC$ 于 $F$.

求证: $EF\\perp BC$.

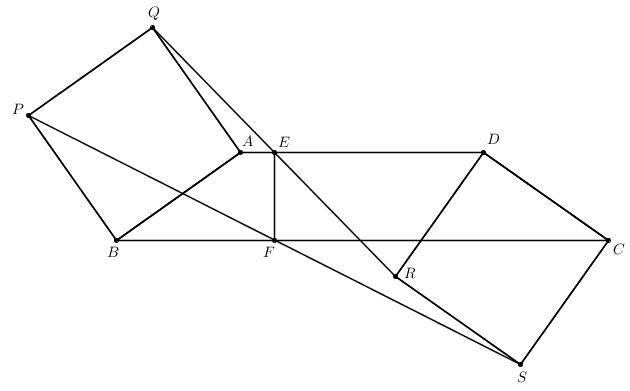
分析:

由等腰梯形及正方形性质, 考虑构造全等三角形.

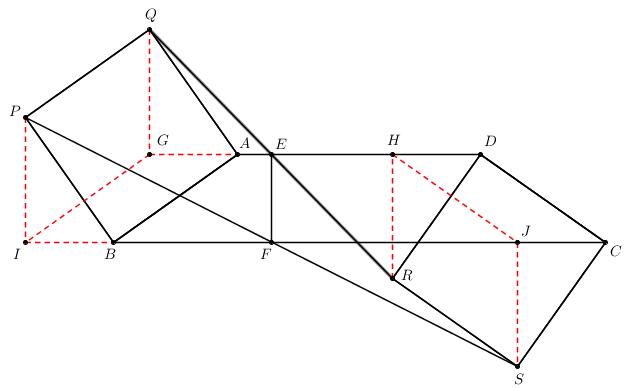
证明:

过 $Q, S$ 分别作 $AH$ 垂线交 $AH$(或其延长线)于 $G, H$.

由 $\\angle{QGA} = \\angle{RHD} = 90^{\\circ},\\ \\angle{AQG} = \\angle{GAB} = \\angle{ABC} = \\angle{DCB} = \\angle{DRH},\\ AQ = AB = CD = DR$,

可得 $\\triangle{AQG} \\cong \\triangle{DRH}$, 进而易证 $\\triangle{EQG}\\cong \\triangle{ERH} \\Rightarrow E$ 是 $GH$ 中点.

同理, 过 $P, S$ 分别作 $BC$ 垂线交 $BC$(或其延长线)于 $I, J$, 易证 $F$ 是 $IJ$ 之中点.

$\\because \\triangle{AQG}\\cong\\triangle{BPI}\\cong\\triangle{DRH}\\cong\\triangle{CSJ}$,

$\\therefore$ 四边形 $GIJH$ 是等腰梯形.

而 $E, F$ 分别是上下底的中点, 故 $EF \\perp BC$.

Q$\\cdot$E$\\cdot$D

 

 

作者微信: zhaoyin0506 (可直接扫描以下二维码)