最短路径之Dijkstra算法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最短路径之Dijkstra算法相关的知识,希望对你有一定的参考价值。
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
一、算法思想
令G = (V,E)为一个带权有向网,把图中的顶点集合V分成两组:已求出最短路径的顶点集合S(初始时S中只有源节点,以后每求得一条最短路径,就将它对应的顶点加入到集合S中,直到全部顶点都加入到S中);未确定最短路径的顶点集合U-(V-S)。在加入过程中,总保持从源节点v到S中各顶点的最短路径长度不大于从源节点v到V-S中任何顶点的最短路径长度。
二、算法描述
(1)S为已经找到的从v出发的最短路径的终点集合,它的初始状态为空集
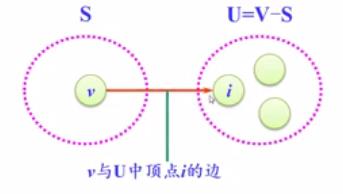
(2)从U中选取一个距离v最小的定点u,把u加入S中,(该选定的距离就是v->u的最短路径长度)
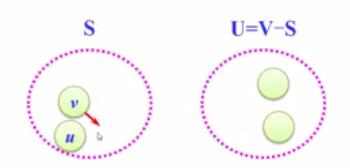
(3)以u为新考虑的中间点,修改U中各顶点j的最短路径长度:若从源点v到顶点j(j∈U)的最短路径长度(经过顶点u)比原来最短路径长度(不经过顶点u)短,则修改顶点j的最短路径长度
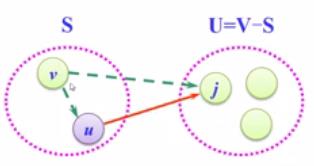
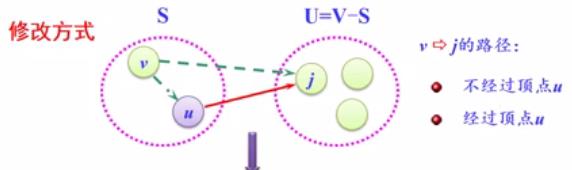
顶点v到j的最短路径=MIN(Cvk+Wkj,Cvj)
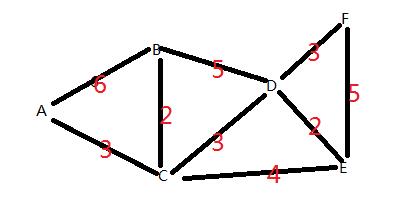
具体执行步骤如下图所示:
| S | U |
DIST[] {A, B, C, D, E, F } |
PATH[] {A, B, C, D, E, F } |
| {A} | {B, C, D, E, F} | {0, 6, 3, ∞, ∞, ∞} | {A, A, A, -1, -1, -1} |
| {A, B, C} | {D, E, F } | {0, 6, 3, 6, 7, ∞} | {A, A, A, C, C, -1} |
| {A,B,C,D,E} | {F} | {0, 6, 3, 6, 7, 9} | {A, A, A, C, C, D} |
| {A,B,C,D,E,F} | {0} | {0, 6, 3, 6, 7, 9} | {A, A, A, C, C, D} |
以上是关于最短路径之Dijkstra算法的主要内容,如果未能解决你的问题,请参考以下文章
最短路径之Dijkstra算法和Floyd-Warshall算法
【数据结构】最短路径之迪杰斯特拉(Dijkstra)算法与弗洛伊德(Floyd)算法