三角函数和解三角形的考向收集整理

Posted tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了三角函数和解三角形的考向收集整理相关的知识，希望对你有一定的参考价值。

三角函数基本变换

  • 此时最常用的公式为二倍角的正弦、余弦公式的逆用，辅助角公式，转化化归为正弦型\\(f(x)=Asin(\\omega x+\\phi)+k\\)

已知函数\\(f(x)=2sinx\\cdot cosx+2\\sqrt{3}\\cdot cos^2x-\\sqrt{3}+1\\)

\\(f(x)=sin2x+\\sqrt{3}(2cos^2x-1)+1\\)

\\(=sin2x+\\sqrt{3}cos2x+1\\)

\\(=2sin(2x+\\cfrac{\\pi}{3})+1\\)

解后反思：

1、熟练掌握这样的变形是非常必要的。

2、当然，此时还可能有一个变形方向，即转化为二次型。比如某个题目可以转化为\\(f(x)=(sinx-1)^2+2\\)，当然这样的变形后，下一步能考查的方向很窄。

三角函数基本性质

  • 此时常常类比模板函数\\(f(x)=sinx\\)的性质求解正弦型\\(f(x)=Asin(\\omega x+\\phi)+k\\)的性质

已知函数\\(f(x)=2sinx\\cdot cosx+2\\sqrt{3}\\cdot cos^2x-\\sqrt{3}+1=2sin(2x+\\cfrac{\\pi}{3})+1\\)

  • 考向：求周期；

由\\(T=\\cfrac{2\\pi}{2}\\)，得到\\(T=\\pi\\)

  • 考向：求值域\\((x\\in R 或 x\\in [-\\cfrac{\\pi}{3}，\\cfrac{\\pi}{4}])\\)；最值(和最值点)；

若\\(x\\in R\\)，则

当\\(sin(2x+\\cfrac{\\pi}{3})=1\\)时，即\\(2x+\\cfrac{\\pi}{3}=2k\\pi+\\cfrac{\\pi}{2}(k\\in Z)\\)，即\\(x=k\\pi+\\cfrac{\\pi}{12}(k\\in Z)\\)时，\\(f(x)_{max}=2\\times1+1=3\\)；

当\\(sin(2x+\\cfrac{\\pi}{3})=-1\\)时，即\\(2x+\\cfrac{\\pi}{3}=2k\\pi-\\cfrac{\\pi}{2}(k\\in Z)\\)，即\\(x=k\\pi-\\cfrac{5\\pi}{12}(k\\in Z)\\)时，\\(f(x)_{max}=2\\times(-1)+1=-1\\)；


若\\(x\\in [-\\cfrac{\\pi}{3}，\\cfrac{\\pi}{4}]\\)，则可得

\\(-\\cfrac{2\\pi}{3}\\leq 2x\\leq \\cfrac{\\pi}{2}\\)，则\\(-\\cfrac{\\pi}{3}\\leq 2x+\\cfrac{\\pi}{3}\\leq \\cfrac{5\\pi}{6}\\)，

故当\\(2x+\\cfrac{\\pi}{3}=-\\cfrac{\\pi}{3}\\)，即\\(x=-\\cfrac{\\pi}{3}\\)时，\\(f(x)_{min}=f(-\\cfrac{\\pi}{3})=2\\times (-\\cfrac{\\sqrt{3}}{2})+1=-\\sqrt{3}+1\\)；

故当\\(2x+\\cfrac{\\pi}{3}=\\cfrac{\\pi}{2}\\)，即\\(x=\\cfrac{\\pi}{12}\\)时，\\(f(x)_{max}=f(\\cfrac{\\pi}{12})=2\\times 1+1=3\\)；

  • 考向：求函数\\(f(x)\\)对称轴方程和对称中心坐标；

令\\(2x+\\cfrac{\\pi}{3}=k\\pi+\\cfrac{\\pi}{2}(k\\in Z)\\)，得到\\(f(x)\\)对称轴方程为\\(x=\\cfrac{k\\pi}{2}+\\cfrac{\\pi}{12}(k\\in Z)\\)；

令\\(2x+\\cfrac{\\pi}{3}=k\\pi(k\\in Z)\\)，得到\\(f(x)\\)的对称中心坐标为\\((\\cfrac{k\\pi}{2}-\\cfrac{\\pi}{6}，1)(k\\in Z)\\)

  • 考向：求奇偶性\\(\\left(奇函数利用f(0)=0；偶函数利用f(0)=f(x)_{max}或f(x)_{min}\\right)\\)

比如，函数\\(g(x)=2sin(2x+\\phi+\\cfrac{\\pi}{3})(\\phi\\in (0，\\pi))\\)是偶函数，求\\(\\phi\\)的值。

分析：由于函数\\(g(x)\\)是偶函数，则在\\(x=0\\)处必然取到最值，

故有\\(2\\times 0+\\phi+\\cfrac{\\pi}{3}=k\\pi+\\cfrac{\\pi}{2}(k\\in Z)\\)，

则\\(\\phi=k\\pi+\\cfrac{\\pi}{6}(k\\in Z)\\)

令\\(k=0\\)，则\\(\\phi=\\cfrac{\\pi}{6}\\in (0，\\pi)\\)，满足题意，故所求\\(\\phi=\\cfrac{\\pi}{6}\\)时，函数\\(g(x)\\)是偶函数。

解后反思：

1、当然，求值域还可能有这样的变形，即转化为二次型。

(2017高考真题 理科全国卷2的第14题)函数\\(f(x)=sin^2x+\\sqrt{3}cosx-\\cfrac{3}{4}(x\\in[0，\\cfrac{\\pi}{2}])\\)的最大值为_______。

分析：由于\\(x\\in[0，\\cfrac{\\pi}{2}]\\)，则\\(cosx\\in [0，1]\\)，

令\\(cosx=t\\in [0，1]\\)，\\(f(x)=1-cos^2x+\\sqrt{3}cosx-\\cfrac{3}{4}=1-t^2+\\sqrt{3}t-\\cfrac{3}{4}=-(t-\\cfrac{\\sqrt{3}}{2})^2+1=g(t)\\)，

故当\\(t=\\cfrac{\\sqrt{3}}{2}\\)时，\\(g(t)_{max}=f(x)_{max}=1\\)。

三角变换解三角形

  • 此时最常用的公式有三角形中的诱导公式、正弦定理、余弦定理，方程理论

(2017高考真题 理科全国卷2的第17题)\\(\\Delta ABC\\) 的内角\\(A，B，C\\)的对边分别是\\(a，b，c\\)，已知\\(sin(A+C)=8sin^2\\cfrac{B}{2}\\)。

(1)求\\(cosB\\).

分析：\\(sin(A+C)=sinB=8\\cdot \\cfrac{1-cosB}{2}\\)，得到\\(sinB=4(1-cosB)\\)，

即\\(\\sqrt{1-cos^2B}=4(1-cosB)\\)，平方得到\\(17cos^2B-32cosB+15=0\\)。

由十字相乘法得到 \\((17cosB-15)(cosB-1)=0\\)，

得到\\(cosB=\\cfrac{15}{17}\\)或\\(cosB=1(舍去)\\)，故\\(cosB=\\cfrac{15}{17}\\)；

(2)若\\(a+c=6\\)，\\(S_{\\Delta ABC}=2\\)，求\\(b\\).

分析：由\\(cosB=\\cfrac{15}{17}\\)得到\\(sinB=\\cfrac{8}{17}\\)，

由\\(S_{\\Delta ABC}=\\cfrac{1}{2}acsinB=2\\)得到，\\(ac=\\cfrac{17}{2}\\)，

故\\(b^2=a^2+c^2-2accosB=(a+c)^2-2ac-2accosB=6^2-2\\cdot \\cfrac{17}{2}-2\\cdot \\cfrac{17}{2}\\cdot\\cfrac{15}{17}=4\\)，

故\\(b=2\\)。

三角变换+函数性质

  • 此时最常用的公式为二倍角的正弦、余弦公式的逆用，辅助角公式，以及整体思想和赋值法；2018年首次出现和导数结合的题型。

(2016.天津高考)已知函数\\(f(x)=4tanx\\cdot sin(\\cfrac{\\pi}{2}-x)\\cdot cos(x-\\cfrac{\\pi}{3})-\\sqrt{3}\\)，试讨论\\(f(x)\\)在区间\\([-\\cfrac{\\pi}{4}，\\cfrac{\\pi}{4}]\\)上的单调性。

解析：先将所给函数化简为正弦型或者余弦型，

\\(f(x)=4tan\\cdot cosx(cosx\\cdot \\cfrac{1}{2}+sinx\\cdot \\cfrac{\\sqrt{3}}{2})-\\sqrt{3}\\)

\\(=4sinx(cosx\\cdot \\cfrac{1}{2}+sinx\\cdot \\cfrac{\\sqrt{3}}{2})-\\sqrt{3}=2sinxcosx+2\\sqrt{3}sin^2x-\\sqrt{3}\\)

\\(=sin2x+\\sqrt{3}(1-cos2x)-\\sqrt{3}=sin2x-\\sqrt{3}cos2x\\)

\\(=2sin(2x-\\cfrac{\\pi}{3})\\)

法1：先求解函数在\\(x\\in R\\)上的单调区间，

令\\(2k\\pi-\\cfrac{\\pi}{2}\\leq 2x-\\cfrac{\\pi}{3}\\leq 2k\\pi+\\cfrac{\\pi}{2}(k\\in Z)\\)，

得到单调递增区间为\\([k\\pi-\\cfrac{\\pi}{12}，k\\pi+\\cfrac{5\\pi}{12}](k\\in Z)\\)，

又因为\\(x\\in [-\\cfrac{\\pi}{4}，\\cfrac{\\pi}{4}]\\)

然后给\\(k\\)赋值，令\\(k=0\\)，

得到函数在区间\\([-\\cfrac{\\pi}{12}，\\cfrac{\\pi}{4}]\\)上单调递增，在区间\\([-\\cfrac{\\pi}{4}，-\\cfrac{\\pi}{12}]\\)上单调递减。

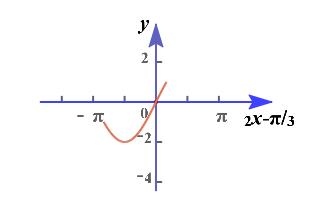
法2：由\\(-\\cfrac{\\pi}{4}\\leq x\\leq \\cfrac{\\pi}{4}\\)，求得\\(-\\cfrac{5\\pi}{6}\\leq 2x-\\cfrac{\\pi}{3}\\leq \\cfrac{\\pi}{6}\\)，

结合横轴为\\(2x-\\cfrac{\\pi}{3}\\)的图像可知，

当\\(-\\cfrac{5\\pi}{6}\\leq 2x-\\cfrac{\\pi}{3}\\leq -\\cfrac{\\pi}{2}\\)时，求得函数在区间\\([-\\cfrac{\\pi}{4}，-\\cfrac{\\pi}{12}]\\)单调递减；

当\\(-\\cfrac{\\pi}{2}\\leq 2x-\\cfrac{\\pi}{3}\\leq \\cfrac{\\pi}{6}\\)时，求得函数在区间\\([-\\cfrac{\\pi}{12}，\\cfrac{\\pi}{4}]\\)单调递增；

【2018高考一卷第16题】求\\(f(x)=2sinx+sin2x\\)的最小值。【最值和导数相结合的题型】

法1：\\(f\'(x)=2cosx+2cos2x=2cosx+2(2cos^2x-1)\\)

\\(=4cos^2x+2cosx-2=(2cosx+2)(2cosx-1)\\)

\\(=4(cosx+1)(cosx-\\cfrac{1}{2})\\)

注意到\\(cosx+1\\ge 0\\)恒成立，故

令\\(f\'(x)>0\\)得到，\\(cosx>\\cfrac{1}{2}\\)，令\\(f\'(x)<0\\)得到，\\(cosx<\\cfrac{1}{2}\\)，

则\\(x\\in [2k\\pi-\\cfrac{5\\pi}{3}，2k\\pi-\\cfrac{\\pi}{3}](k\\in Z)\\)时，函数\\(f(x)\\)单调递减；

\\(x\\in [2k\\pi-\\cfrac{\\pi}{3}，2k\\pi+\\cfrac{\\pi}{3}](k\\in Z)\\)时，函数\\(f(x)\\)单调递增；

故当\\(x=2k\\pi-\\cfrac{\\pi}{3}(k\\in Z)\\)时，\\(f(x)_{min}=f(2k\\pi-\\cfrac{\\pi}{3})=-\\cfrac{3\\sqrt{3}}{2}\\)。

三角形周长面积

  • 此时往往已经知道三角形的一条边和其对角，使用面积公式求面积，由余弦定理求得另外两边长之和，从而求得周长。

(2017\\(\\cdot\\)全国卷I)

已知\\(\\Delta ABC\\)的内角\\(A，B，C\\)的对边分别是\\(a，b，c\\)，\\(S_{\\Delta ABC}=\\cfrac{a^2}{3sinA}\\)；

(1)求\\(sinBsinC\\)的值；

(2)若\\(6cosBcosC=1\\)，\\(a=3\\)，求\\(\\Delta ABC\\)的周长；

分析：(1)由\\(S_{\\Delta ABC}=\\cfrac{1}{2}acsinB=\\cfrac{a^2}{3sinA}\\)，

变形得到\\(\\cfrac{1}{2}csinB=\\cfrac{a}{3sinA}\\)，

边化角，得到\\(\\cfrac{1}{2}sinCsinB=\\cfrac{sinA}{3sinA}\\)，

故\\(sinBsinC=\\cfrac{2}{3}\\)。

(2)由于求三角形周长的题目，一般都会知道一条边和其对角，现在知道了边\\(a\\)，故猜想应该能求得\\(A\\)，

这样想，我们一般就会将条件作差而不是作商，

由\\(cosBcosC-sinBsinC=-\\cfrac{1}{2}\\)，

即\\(cos(B+C)=-cosA=-\\cfrac{1}{2}\\)，得到\\(A=\\cfrac{\\pi}{3}\\)；

由题意\\(\\cfrac{1}{2}bcsinA=\\cfrac{a^2}{3sinA}\\)，\\(a=3\\)

得到\\(bc=8\\)；

再由余弦定理得到\\(a^2=b^2+c^2-2bccosA\\)，

得到\\(3^2=(b+c)^2-2bc-2bccosA\\)，即\\(b+c=\\sqrt{33}\\)；

故周长为\\(3+\\sqrt{33}\\)。

面积最大值或边最小值

  • 此时往往可以利用均值不等式求最值或者利用三角函数求最值

【三轮模拟考试理科用题】在\\(\\Delta ABC\\)中，已知\\(4cos^2\\cfrac{A}{2}-cos2(B+C)=\\cfrac{7}{2}，a=2\\)，则\\(\\Delta ABC\\)的面积的最大值为________.

分析：由\\(cos2(B+C)=cos(2B+2C)=cos(2\\pi-2A)=cos2A\\)，

将已知等式变形为\\(2\\cdot 2cos^2\\cfrac{A}{2}-cos2A=\\cfrac{7}{2}\\)，

即\\(2(1+cosA)-cos2A=\\cfrac{7}{2}\\)，

即\\(2(1+cosA)-(2cos^2A-1)=\\cfrac{7}{2}\\)，

化简为\\(4cos^2A-4cosA+1=(2cosA-1)^2=0\\)，

解得\\(cosA=\\cfrac{1}{2}，A\\in(0，\\pi)\\)，故\\(A=\\cfrac{\\pi}{3}\\)，

到此题目转化为已知\\(A=\\cfrac{\\pi}{3}，a=2\\)，求\\(\\Delta ABC\\)的面积的最大值。

接下来有两个思路途径：

思路一：使用均值不等式，由余弦定理\\(a^2=b^2+c^2-2bccosA，A=\\cfrac{\\pi}{3}，a=2\\)

得到\\(b^2+c^2=4+bc\\ge 2bc\\)，解得\\(bc\\leq 4(当且仅当b=c=2时取到等号)\\)，

则\\(S_{\\Delta ABC}=\\cfrac{1}{2}bcsinA \\leq \\cfrac{\\sqrt{3}}{4}\\times 4=\\sqrt{3}\\)。

即三角形面积的最大值是\\(\\sqrt{3}\\)。

法2：由于题目已知\\(A=\\cfrac{\\pi}{3}，a=2\\)，则\\(B+C=\\cfrac{2\\pi}{3}\\)，故\\(B，C\\in (0，\\cfrac{2\\pi}{3})\\)，

则由正弦定理得\\(\\cfrac{b}{sinB}=\\cfrac{c}{sinC} =\\cfrac{a}{sinA} =\\cfrac{2}{\\frac{\\sqrt{3}}{2}} =\\cfrac{4\\sqrt{3}}{3}\\)，

则\\(b=\\cfrac{4\\sqrt{3}}{3}sinB\\)，\\(c=\\cfrac{4\\sqrt{3}}{3}sinC\\)，

则\\(bc=(\\cfrac{4\\sqrt{3}}{3})^2\\cdot sinB\\cdot sinC=\\cfrac{16}{3}sinB\\cdot sin(\\cfrac{2\\pi}{3}-B)\\)

\\(=\\cfrac{16}{3}sinB\\cdot (\\cfrac{\\sqrt{3}}{2}cosB+\\cfrac{1}{2}sinB)\\)

\\(=\\cfrac{16}{3}[\\cfrac{\\sqrt{3}}{2}sinB\\cdot cosB+\\cfrac{1}{2}sin^2B]\\)

\\(=\\cfrac{16}{3}[\\cfrac{\\sqrt{3}}{4}sin2B+\\cfrac{1}{4}(1-cos2B)]\\)

\\(=\\cfrac{16}{3}(\\cfrac{\\sqrt{3}}{4}sin2B-\\cfrac{1}{4}cos2B+\\cfrac{1}{4})\\)

\\(=\\cfrac{8}{3}(sin2B\\cdot \\cfrac{\\sqrt{3}}{2}-cos2B\\cdot \\cfrac{1}{2})+\\cfrac{4}{3}\\)

\\(=\\cfrac{8}{3}sin(2B-\\cfrac{\\pi}{6})+\\cfrac{4}{3}\\)

当\\(2B-\\cfrac{\\pi}{6}=\\cfrac{\\pi}{2}\\)，即\\(B=\\cfrac{5\\pi}{12} \\in(0，\\cfrac{2\\pi}{3})\\)时，\\(sin(2B-\\cfrac{\\pi}{6})=1\\)，

即\\(bc_{max}=\\cfrac{8}{3}+\\cfrac{4}{3}=4\\)

故\\([S_{\\Delta}]_{max}=\\cfrac{1}{2}bcsinA\\leq \\cfrac{\\sqrt{3}}{4}\\times 4=\\sqrt{3}\\)。

解后反思：求某边的最小值，比如已知\\(ac=4\\)，\\(B=\\cfrac{\\pi}{3}\\)，

则\\(b^2=a^2+c^2-2accosB=a^2+c^2-ac\\ge 2ac-ac=ac=4\\)，即\\(b^2\\ge 4\\)，即\\(b_{min}=2\\)

三角形周长最大值

  • 此时常利用均值不等式或三角函数求最大值

【三角函数图像性质和解三角形结合】【2017•福州模拟】在\\(\\Delta ABC\\)中，角\\(A，B，C\\)的对边分别为\\(a，b，c\\)，满足\\((2b-c)\\cdot cosA=a\\cdot cosC\\)。　

(1)求角\\(A\\)的大小；(考查角度：解三角形)

(2)若\\(a=3\\)，求\\(\\Delta ABC\\)的周长的最大值。(考查角度：三角函数图像性质)

分析：(1)由\\((2b-c)\\cdot cosA=a\\cdot cosC\\)及正弦定理，边化角得到，

得\\((2sinB-sinC)cosA=sinAcosC\\)，

所以\\(2sinBcosA=sinCcosA+sinAcosC\\)， 所以\\(2sinBcosA=sin(C+A)=sinB\\)，

因为\\(B\\in (0，π)\\)，所以\\(sinB\\neq 0\\)，

因为\\(A\\in (0，π)\\)，\\(cosA=\\cfrac{1}{2}\\)，所以$A=\\cfrac{\\pi}{3} $。

(2)由(1)得$A=\\cfrac{\\pi}{3} $，

由正弦定理得\\(\\cfrac{b}{sinB}=\\cfrac{c}{sinC} =\\cfrac{a}{sinA} =\\cfrac{3}{\\frac{\\sqrt{3}}{2}} =2\\sqrt{3}\\)，

所以\\(b=2\\sqrt{3}\\cdot sinB\\)； \\(c=2\\sqrt{3}\\cdot sinC\\)，

\\(\\Delta ABC\\)的周长：\\(l=3+2\\sqrt{3}\\cdot sinB+2\\sqrt{3}\\cdot sinC\\)

\\(=3+2\\sqrt{3}\\cdot sinB+2\\sqrt{3}\\cdot sin(\\cfrac{2\\pi}{3}-B)\\)

\\(=3+2\\sqrt{3}\\cdot sinB+2\\sqrt{3}\\cdot (\\cfrac{\\sqrt{3}}{2}cosB+\\cfrac{1}{2}sinB)\\)

\\(=3+3\\sqrt{3}sinB+3cosB=3+6sin(B+\\cfrac{\\pi}{6})\\)

因为\\(B\\in(0，\\cfrac{2\\pi}{3})\\)，所以当\\(B=\\cfrac{\\pi}{3}\\) 时，\\(\\Delta ABC\\)的周长取得最大值，最大值为9。

表达式取值范围

  • 此时常利用三角函数求最大值

(2016宝鸡市第二次质量检测第17题)在\\(\\Delta ABC\\)中，已知\\(sin^2A+sin^2B+sinAsinB=sin^2C\\)，其中角\\(A、B、C\\)的对边分别为\\(a、b、c\\)，

(1).求角\\(C\\)的大小。

(2).求\\(\\cfrac{a+b}{c}\\)的取值范围。

分析：(1)角化边，由\\(\\cfrac{a}{2R}=sinA，\\cfrac{b}{2R}=sinB，\\cfrac{c}{2R}=sinC\\)

得到\\(a^2+b^2+ab=c^2\\)，即\\(a^2+b^2-c^2=-ab\\)，

故由余弦定理得到\\(cosC=\\cfrac{a^2+b^2-c^2}{2ab}=-\\cfrac{1}{2}\\)，

又\\(C\\in (0，\\pi)\\)，故\\(C=\\cfrac{2\\pi}{3}\\)。

(2)由(1)可知，\\(A+B=\\cfrac{\\pi}{3}\\)，即\\(A=\\cfrac{\\pi}{3}-B\\)

边化角，由\\(a=2RsinA，b=2RsinB，c=2RsinC\\)

\\(\\cfrac{a+b}{c}=\\cfrac{sinA+sinB}{sinC}=\\cfrac{2\\sqrt{3}}{3}(sinA+sinB)\\)

\\(=\\cfrac{2\\sqrt{3}}{3}[sin(\\cfrac{\\pi}{3}-B)+sinB]=\\cfrac{2\\sqrt{3}}{3}[\\cfrac{\\sqrt{3}}{2}cosB-\\cfrac{1}{2}sinB+sinB]\\)

\\(=\\cfrac{2\\sqrt{3}}{3}(\\cfrac{1}{2}sinB+\\cfrac{\\sqrt{3}}{2}cosB)=\\cfrac{2\\sqrt{3}}{3}sin(B+\\cfrac{\\pi}{3})\\)，

又由\\(\\begin{cases}B >0\\\\ \\cfrac{\\pi}{3}-B >0\\end{cases}\\)得到\\(0< B <\\cfrac{\\pi}{3}\\)，

故\\(\\cfrac{\\pi}{3}< B+\\cfrac{\\pi}{3} <\\cfrac{2\\pi}{3}\\)，

则\\(\\cfrac{\\sqrt{3}}{2} < sin(B+\\cfrac{\\pi}{3})\\leq 1\\)

则有\\(1<\\cfrac{\\sqrt{3}}{2}\\cdot sin(B+\\cfrac{\\pi}{3})\\leq \\cfrac{2\\sqrt{3}}{3}\\)

即\\(\\cfrac{a+b}{c}\\)的取值范围为\\((1，\\cfrac{2\\sqrt{3}}{3}]\\)。

引申：上述思路可以求解\\(msinB+nsinC\\)的取值范围(\\(m、n\\)是实数)。

在锐角三角形\\(ABC\\)中，\\(C=2B\\),则\\(\\cfrac{c}{b}\\)的取值范围是\\((\\sqrt{2}，\\sqrt{3}）\\)

分析：本题先将\\(\\cfrac{c}{b}=\\cfrac{sinC}{sinB}=2cosB\\)，

接下来的难点是求\\(B\\)的范围，注意列不等式的角度，锐角三角形的三个角都是锐角，要同时限制

由\\(\\begin{cases}&0< A <\\cfrac{\\pi}{2} \\\\ &0 < B <\\cfrac{\\pi}{2} \\\\ &0< C <\\cfrac{\\pi}{2}\\end{cases}\\)得到，

\\(\\begin{cases} &0 < \\pi-3B <\\cfrac{\\pi}{2} \\\\ &0 < B <\\cfrac{\\pi}{2} \\\\ &0 < 2B <\\cfrac{\\pi}{2}\\end{cases}\\)

解得\\(B \\in (\\cfrac{\\pi}{6}，\\cfrac{\\pi}{4})\\)，故\\(\\cfrac{c}{b}=2cosB \\in (\\sqrt{2}，\\sqrt{3}）\\)。

在锐角\\(\\Delta ABC\\)中，内角\\(A、B、C\\)的对边分别是\\(a、b、c\\)，且满足\\((a-b)(sinA+sinB)=(c-b)sinC\\)，若\\(a=\\sqrt{3}\\)，则\\(b^2+c^2\\)的取值范围是【】

\\(A.(3，6]\\). \\(\\hspace{4em}\\) \\(B.(3，5)\\). \\(\\hspace{4em}\\) \\(C.(5，6]\\). \\(\\hspace{4em}\\) \\(D.[5，6]\\).

分析：由已知和正弦定理可知，

\\((a-b)(a+b)=(c-b)c\\)，即\\(bc=b^2+c^2-a^2\\)，

故\\(cosA=\\cfrac{1}{2}\\)，由\\(A\\in (0，\\pi)\\)，可知\\(A=\\cfrac{\\pi}{3}\\)。

则\\(B+C=\\cfrac{2\\pi}{3}\\)，又由于是锐角\\(\\Delta ABC\\)，

则\\(\\left\\{\\begin{array}{l}{0< B < \\cfrac{\\pi}{2}}\\\\{0<\\cfrac{2\\pi}{3}-B < \\cfrac{\\pi}{2}}\\end{array}\\right.\\)

则得到\\(\\cfrac{\\pi}{6}< B < \\cfrac{\\pi}{2}\\)；

又\\(a=\\sqrt{3}\\)，则\\(2R=\\cfrac{a}{sinA}=2\\)，

所以\\(b^2+c^2=(2RsinB)^2+(2RsinC)^2\\)

\\(=(2R)^2(sin^2B+sin^2C)\\)

\\(=4(sin^2B+sin^2(\\cfrac{2\\pi}{3}-B))\\)

\\(=4[sin^2B+(\\cfrac{\\sqrt{3}}{2}cosB+\\cfrac{1}{2}sinB)^2]\\)

\\(=4(sin^2B+\\cfrac{3}{4}cos^2B+\\cfrac{1}{4}sin^2B+2\\cdot \\cfrac{\\sqrt{3}}{2}cosB\\cdot \\cfrac{1}{2}sinB)\\)

\\(=4(\\cfrac{3}{4}+\\cfrac{1}{2}sin^2B+\\cfrac{\\sqrt{3}}{4}sin2B)\\)

\\(=4[\\cfrac{1}{4}(1-cos2B)+\\cfrac{\\sqrt{3}}{4}sin2B+\\cfrac{3}{4}]\\)

\\(=\\sqrt{3}sin2B-cos2B+4\\)

\\(=2sin(2B-\\cfrac{\\pi}{6})+4\\)，

由上可知，\\(\\cfrac{\\pi}{6}< B < \\cfrac{\\pi}{2}\\)，

则\\(\\cfrac{\\pi}{3}< 2B <\\pi\\)，

\\(\\cfrac{\\pi}{6}< 2B-\\cfrac{\\pi}{6} < \\cfrac{5\\pi}{6}\\)

则\\(\\cfrac{1}{2}< sin(2B-\\cfrac{\\pi}{6})\\leq 1\\)

则\\(5<2sin(2B-\\cfrac{\\pi}{6})+4\\leq 6\\)，故选C。

三角函数向量融合

  • 此时常考查向量的坐标运算和三角变换，转化为正弦型后再考察其性质

【三角函数和解三角形和向量结合】已知函数\\(f(x)=cosxsinx-\\sqrt{3}cos^2x+\\cfrac{\\sqrt{3}}{2}\\)，

(1)求函数\\(f(x)\\)的单调递增区间

分析：函数化简为\\(f(x)=sin(2x-\\cfrac{\\pi}{3})\\)，过程略，\\([k\\pi-\\cfrac{\\pi}{12}，k\\pi+\\cfrac{5\\pi}{12}](k\\in Z)\\)

(2)在\\(\\Delta ABC\\)中，\\(A\\)为锐角且\\(f(A)=\\cfrac{\\sqrt{3}}{2}\\)，\\(\\overrightarrow{AB}+\\overrightarrow{AC}=3\\overrightarrow{AD}\\)，\\(AB=\\sqrt{3}\\)，\\(AD=2\\)，求\\(sin\\angle BAD\\)。

分析：由\\(f(A)=sin(2A-\\cfrac{\\pi}{3})=\\cfrac{\\sqrt{3}}{2}\\)，解得\\(A=\\cfrac{\\pi}{3}\\)或\\(A=\\cfrac{\\pi}{2}\\)(舍去)。

又由于\\(\\overrightarrow{AB}+\\overrightarrow{AC}=3\\overrightarrow{AD}\\)，如图所示，

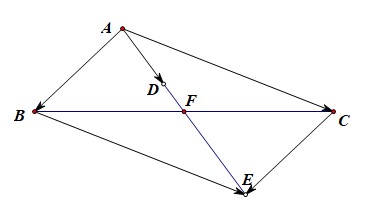
\\(\\overrightarrow{AB}+\\overrightarrow{AC}=\\overrightarrow{AE}=2\\overrightarrow{AF}=2\\cdot \\cfrac{3}{2}\\overrightarrow{AD}=3\\overrightarrow{AD}\\)，

故点\\(D\\)为\\(\\triangle ABC\\)的重心，详细说明\\(\\;\\;\\)[1] (点击这个蓝色的数字)

以\\(AB\\)、\\(AC\\)为邻边做平行四边形\\(ABEC\\)，由于\\(AD=2\\)，则\\(AE=6\\)，

在\\(\\Delta ABE\\)中，\\(AB=\\sqrt{3}\\)，\\(\\angle ABE=120^{\\circ}\\)，

由正弦定理可得，\\(\\cfrac{\\sqrt{3}}{sin\\angle AEB}=\\cfrac{6}{\\cfrac{\\sqrt{3}}{2}}\\)，

可得\\(sin\\angle AEB=\\cfrac{1}{4}\\) ，\\(cos\\angle AEB=\\cfrac{\\sqrt{15}}{4}\\)，

故\\(sin\\angle BAD=sin(\\cfrac{\\pi}{3}-\\angle AEB)\\)

\\(=\\cfrac{\\sqrt{3}}{2}\\times \\cfrac{\\sqrt{15}}{4}-\\cfrac{1}{2}\\times \\cfrac{1}{4}=\\cfrac{3\\sqrt{5}-1}{8}\\)。

解后反思：利用已知的向量三角形，巧妙的构造了一个三角形，这样就能利用正弦定理和两角差的正弦公式求解了。

四边形边的范围

  • 将四边形动态变化为三角形，从而求解四边形的某条边的取值范围

【2015\\(\\cdot\\)全国卷Ⅰ】在平面四边形\\(ABCD\\)中，\\(\\angle A=\\angle B=\\angle C=75^{\\circ}\\)，\\(BC=2\\)，则\\(AB\\)的取值范围是___________。

分析：本题目非常特别，依据题意我们做出的图形是平面四边形，

当我们将边\\(AD\\)平行移动时，题目的已知条件都没有改变，故想到将此静态图变化为动态图，

平行移动\\(AD\\)时，我们看到了两个临界位置，即四边形变化为三角形的两个状态，

其一是四边形变化为三角形\\(ABF\\)，此时应该有\\(BF<AB\\)；

其二是四边形变化为三角形\\(ABE\\)，此时应该有\\(BE>AB\\)；

故动态的边\\(AB\\)的范围是\\(BF<AB<BE\\)，从而求解。

解答：如图所示，延长\\(BA\\)与\\(CD\\)交于\\(E\\)，过\\(C\\)做\\(CF//AD\\)交\\(AB\\)于\\(F\\)，则\\(BF<AB<BE\\)；

在等腰三角形\\(CFB\\)中，\\(\\angle FCB=30^{\\circ}\\)，\\(CF=BC=2\\)，由余弦定理得到\\(BF=\\sqrt{6}-\\sqrt{2}\\)；

在等腰三角形\\(ECB\\)中，\\(\\angle CEB=30^{\\circ}\\)，\\(\\angle ECB=75^{\\circ}\\)，\\(BE=CE，BC=2\\)，

由正弦定理得到\\(BE=\\sqrt{6}+\\sqrt{2}\\)；

故\\(\\sqrt{6}-\\sqrt{2}<AB<\\sqrt{6}+\\sqrt{2}\\)

解后反思引申：

1、求\\(CD\\)的取值范围；

分析：由上述的动态图可知，\\(0<CD<CE=BE=\\sqrt{6}+\\sqrt{2}\\)；

2、求\\(AD\\)的取值范围；

分析：由上述的动态图可知，\\(0<AD<CF=BC=2\\)；

3、求四边形\\(ABCD\\)的周长的取值范围；

分析：四边形\\(ABCD\\)的周长介于\\(\\Delta BCF\\)的周长和\\(\\Delta BCE\\)的周长之间，

故其取值范围是\\((4+\\sqrt{6}-\\sqrt{2}，2(\\sqrt{6}+\\sqrt{2})+2)\\)；

4、求四边形\\(ABCD\\)的面积的取值范围；

分析：四边形\\(ABCD\\)的面积介于\\(\\Delta BCF\\)的面积和\\(\\Delta BCE\\)的面积之间，

\\(S_{\\Delta BCF}=\\cfrac{1}{2}\\times 2\\times 2\\times sin30^{\\circ}=1\\)；

\\(S_{\\Delta BCE}=\\cfrac{1}{2}\\times (\\sqrt{6}+\\sqrt{2})\\times (\\sqrt{6}+\\sqrt{2})\\times sin30^{\\circ}=2+\\sqrt{3}\\)；

故其取值范围是\\((1，2+\\sqrt{3})\\)；

三角函数和恒成立命题

  • 先将恒成立问题转化为最值，这样原问题就转化为三角函数的问题了

【2018宝鸡市二检文科理科第17题】已知函数\\(f(x)=4sinxsin(x+\\cfrac{\\pi}{3})\\)，在\\(\\Delta ABC\\)中，角\\(A、B、C\\)的对边分别是\\(a、b、c\\)，

(1)、当\\(x\\in [0，\\cfrac{\\pi}{2}]\\)时，求函数\\(f(x)\\)的取值范围。

分析：先将函数变形为正弦型函数\\(f(x)=2sin(2x-\\cfrac{\\pi}{6})+1\\)，其中\\(x\\in [0，\\cfrac{\\pi}{2}]\\)，

题目转化为正弦型函数在限定区间上的值域问题，常规题目，\\(f(x)\\in [0，3]\\)

(2)、若对任意的\\(x\\in R\\)，都有\\(f(x)\\leq f(A)\\)，\\(b=2\\)，\\(c=4\\)，点\\(D\\)是边\\(BC\\)的中点，求\\(AD\\)的长。

【解答的共有部分】对任意的\\(x\\in R\\)，都有\\(f(x)\\leq f(A)\\)，则\\(f(A)\\geqslant f(x)_{max}\\)；

\\(f(x)=2sin(2x-\\cfrac{\\pi}{6})+1，x\\in R\\)，则\\(f(x)_{max}=3\\)，

即\\(f(A)\\geqslant 3\\)又\\(f(A)=2sin(2A-\\cfrac{\\pi}{6})+1\\)

故有\\(2sin(2A-\\cfrac{\\pi}{6})+1\\geqslant 3\\)，即\\(sin(2A-\\cfrac{\\pi}{6})\\geqslant 1\\)，

又由正弦函数的值域范围可知，此时只能取\\(sin(2A-\\cfrac{\\pi}{6})=1\\)，

即\\(2A-\\cfrac{\\pi}{6}=\\cfrac{\\pi}{2}\\)，故\\(A=\\cfrac{\\pi}{3}\\)。

【法1】：余弦定理法，先由余弦定理得到\\(BC=2\\sqrt{3}\\)，则\\(BD=CD=\\sqrt{3}\\)，

设\\(\\angle ADB=\\alpha\\)，\\(\\angle ADC=\\beta\\)，则有\\(cos\\alpha+cos\\beta=0\\)。

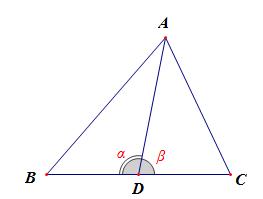
再设\\(AD=x\\)，又\\(cos\\alpha=\\cfrac{x^2+(\\sqrt{3})^2-4^2}{2\\cdot\\sqrt{3}\\cdot x}\\)；\\(cos\\beta=\\cfrac{x^2+(\\sqrt{3})^2-2^2}{2\\cdot\\sqrt{3}\\cdot x}\\)；

代入方程\\(cos\\alpha+cos\\beta=0\\)得到，\\(x=AD=\\sqrt{7}\\)。

【法2】：要求\\(AD\\)，由\\(AD=|\\overrightarrow{AD}|\\)，而\\(|\\overrightarrow{AD}|=\\sqrt{\\overrightarrow{AD}^2}\\)，

\\(\\overrightarrow{AD}=\\cfrac{1}{2}(\\overrightarrow{AB}+\\overrightarrow{AC})\\)，则\\(\\overrightarrow{AD}^2=\\cfrac{1}{4}(\\overrightarrow{AB}+\\overrightarrow{AC})^2\\)

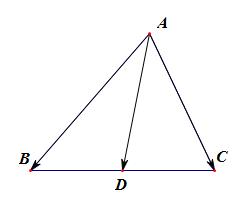
则\\(|\\overrightarrow{AD}|^2=\\cfrac{1}{4}(|\\overrightarrow{AB}|^2+|\\overrightarrow{AC}|^2+2|\\overrightarrow{AB}||\\overrightarrow{AC}|cos60^{\\circ})\\)

\\(=\\cfrac{1}{4}(4^2+2^2+2\\times4\\times2\\times\\cfrac{1}{2})=7\\)

故\\(AD=|\\overrightarrow{AD}|=\\sqrt{7}\\)；

【法3】由题目可知，先由余弦定理得到\\(BC=2\\sqrt{3}\\)，则由\\(AB=4，AC=2\\)，可知\\(\\Delta ABC\\)为\\(Rt\\Delta\\)，

则有\\(AC=2\\)，\\(CD=\\sqrt{3}\\)，故由勾股定理可知，\\(AD=\\sqrt{7}\\)。

解后反思：1、向量法和余弦定理法都是大家应该掌握的常见的思路方法，其中向量法这个思路，对学生和老师而言，都不是那样的自如应用。

解三角形应用

  • 此时常先建立解三角形的数学模型，然后利用正余弦定理求解，需要注意立体问题平面化，不同三角形中的要素统一化到同一个三角形中。

解三角形的实际应用

  1. 可以直接使用的结论：
    在\\(\\triangle ABC\\)中，若已知\\(\\overrightarrow{AB}+\\overrightarrow{AC}=2\\overrightarrow{AE}\\)，则可知点\\(E\\)为边\\(BC\\)的中点；
    在\\(\\triangle ABC\\)中，已知\\(\\overrightarrow{AB}+\\overrightarrow{AC}=3\\overrightarrow{AD}\\)，可知点\\(D\\)为\\(\\triangle ABC\\)的重心；
    具体解释如下图所示，
    若已知\\(\\overrightarrow{AB}+\\overrightarrow{AC}=2\\overrightarrow{AE}\\)，或者\\(\\overrightarrow{AE}=\\cfrac{1}{2}(\\overrightarrow{AB}+\\overrightarrow{AC})\\)，则可知点\\(E\\)为\\(BC\\)的中点；

    已知\\(\\overrightarrow{AB}+\\overrightarrow{AC}=3\\overrightarrow{AD}\\)，则\\(3\\overrightarrow{AD}=2\\overrightarrow{AE}\\)，则\\(\\overrightarrow{AD}=\\cfrac{2}{3}\\overrightarrow{AE}\\)，可知点\\(D\\)为\\(\\triangle ABC\\)的重心； ↩︎

以上是关于三角函数和解三角形的考向收集整理的主要内容，如果未能解决你的问题，请参考以下文章

三角函数公式整理

重新整理：纯CSS写三角形

数学知识整理：三角函数公式复习

python中*和**的打包和解包

python中*和**的打包和解包

一图看懂 bz2 模块：处理压缩和解压缩文件, 资料整理+笔记（大全）