简介
- 算法导论第四章介绍过使用分治法求最大子数组问题,其基本思想就是把一个数组分成三部分,a[0:n/2],a[n/2+1:n],a[j:k] (其中0<=j<=n/2,n/2+1<=k<=n),通过递归分别求出他们的最大子数组和,然后再从中挑出最大的一个值,即为该数组的最大子数组值,该算法的时间复杂度为O(nlogn)
- 白盒测试有语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖这五个覆盖标准
- 环境:Ubuntu 16.04
- 语言:C++
- 测试工具:GTest(Gtest框架搭建教程)
一.问题
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
--引用《百度百科》
大家可以参照算法导论第四章或者是这里或者我的Github,来查看具体如何实现,这里主要给大家展示功能函数模块和测试该函数模块
二.功能函数模块
//max_array.cpp
#include<iostream>
#include "gtest/gtest.h"
using namespace std;
/**
*功能函数
*@author Stone
*version 1.0
*/
//得到最大中子数组
int FIND_MAX_CROSSING_SUBARRAY(int a[], int low, int mid, int high)
{
int sum = 0;
int left_sum, right_sum;
int max_left, max_right;
int i, j;
left_sum = right_sum = -1000;//使左右子数组和为无穷小,假设数组和不会小于-1000
for(i = mid; i >= low; i--)
{
sum = sum + a[i];
if(sum > left_sum)
{
left_sum = sum;
max_left = i;
}
}
sum = 0;
for(j = mid+1; j <= high; j++)
{
sum = sum +a[j];
if(sum > right_sum)
{
right_sum = sum;
max_right = j;
}
}
low = max_left;
high = max_right;
sum = left_sum + right_sum;
return sum;
}
//传进去数组,数组的低位序号,高位序号,返回最大子数组
int FIND_MAXIMUM_SUBARRAY(int a[], int low, int high)
{
int left_sum, right_sum, cross_sum;
//低位序号和高位序号相同
if(low == high)
{
return a[low];
}
else
{
int mid;
mid = (low + high)/2;
left_sum = FIND_MAXIMUM_SUBARRAY(a, low, mid);//得到最大左子数组
right_sum = FIND_MAXIMUM_SUBARRAY(a, mid+1, high);//得到最大右子数组
cross_sum = FIND_MAX_CROSSING_SUBARRAY(a, low, mid, high);//得到最大中子数组
//最大左子数组为最大子数组
if(left_sum >= right_sum && left_sum >= cross_sum)
{
return left_sum;
}
//最大右子数组为最大子数组
else if(right_sum >= left_sum && right_sum >= cross_sum)
{
return right_sum;
}
//最大中子数组为最大子数组
else return cross_sum;
}
}
三.测试
本次测试通过使用白盒测试的条件组合覆盖进行测试,执行足够的测试用例,使得每个判定中条件的各种可能组合都至少出现一次
1.功能函数int FIND_MAXIMUM_SUBARRAY(int a[], int low, int high)流程图
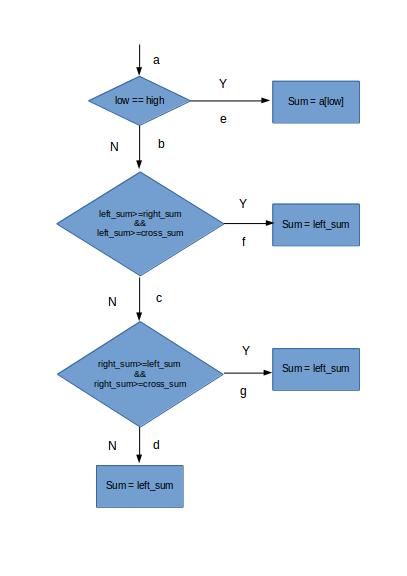
通过流程图知,条件组合覆盖一共有4条路径,分别是ae,abf,abcg,abcd,按照条件组合的定义,共有14种可能的组合,分别是:
low == high
low != high
left_sum >= right_sum,left_sum >= cross_sum
left_sum >= right_sum,left_sum < cross_sum
left_sum < right_sum,left_sum >= cross_sum
left_sum < right_sum,left_sum < cross_sum
right_sum >= left_sum,right_sum >= cross_sum
right_sum >= left_sum,right_sum < cross_sum
right_sum < left_sum,right_sum >= cross_sum
10)right_sum < left_sum,right_sum < cross_sum
11)cross_sum >= left_sum,cross_sum >= right_sum
12)cross_sum >= left_sum,cross_sum < right_sum
- cross_sum < left_sum,cross_sum >= right_sum
14)cross_sum < left_sum,cross_sum < right_sum
这里设置7个测试用例,用以覆盖上述14种条件组合,如下表所示:
| 测试用例 | 数组 | 期待值 | 覆盖组合号 | 执行路径 |
|---|---|---|---|---|
| 测试用例1 | 1 | 1 | 1 | ae |
| 测试用例2 | 5, -3, 2, -3, 1 | 5 | 2,3,10,13 | abf |
| 测试用例3 | -2, 11, -4, 13, -5, -2 | 20 | 2,6,8,11 | abcg |
| 测试用例4 | 3, -4, -3, -7, 5 | 5 | 2,5,7,14 | abcd |
| 测试用例5 | -3, 2, 3, -2, 1 | 5 | 2,4,10,11 | abcg |
| 测试用例6 | -3, -2, 3, -4, 9 | 9 | 2,3,9,12 | abcg |
| 测试用例7 | 5,-4,-2,-3,1 | 5 | 2,3,9,14 | abcd |
2.测试代码
//测试模块
TEST(max_arrayTest0, max_arrayCase0)
{
int a[0];
a[0] = 1;
ASSERT_EQ(1, FIND_MAXIMUM_SUBARRAY(a, 0, 1));
}
TEST(max_arrayTest1, max_arrayCase1)
{
int b[5] = {5, -3, 2, -3, 1};
ASSERT_EQ(5, FIND_MAXIMUM_SUBARRAY(b, 0, 4));
}
//题目中的
TEST(max_arrayTest2, max_arrayCase2)
{
int c[6] = {-2, 11, -4, 13, -5, -2};
ASSERT_EQ(20, FIND_MAXIMUM_SUBARRAY(c, 0, 5));
}
TEST(max_arrayTest3, max_arrayCase3)
{
int d[5] = {3, -4, -3, -1, 10};
ASSERT_EQ(10, FIND_MAXIMUM_SUBARRAY(d, 0, 4));
}
TEST(max_arrayTest4, max_arrayCase4)
{
int e[5] = {-3, 2, 3, -2, 1};
ASSERT_EQ(5, FIND_MAXIMUM_SUBARRAY(e, 0, 4));
}
TEST(max_arrayTest5, max_arrayCase5)
{
int f[5] = {-3, -2, 3, -4, 9};
ASSERT_EQ(9, FIND_MAXIMUM_SUBARRAY(f, 0, 4));
}
TEST(max_arrayTest6, max_arrayCase6)
{
int f[5] = {5, -4, -2, -3, 1};
ASSERT_EQ(5, FIND_MAXIMUM_SUBARRAY(f, 0, 4));
}
int main(int argc, char* argv[])
{
testing::InitGoogleTest(&argc, argv);
return RUN_ALL_TESTS();
}
在终端依次输入:
g++ -o max_array.o -c max_array.cpp -I./include
g++ -o test *.o -I./include -L./lib -lgtest -lpthread
./test

全绿,测试通过!
四.总结
刚开始测试时误解了条件组合覆盖的定义,一直纠结于怎么去对递归进行测试,后来才明白条件组合覆盖是要求使得每个判定中的条件的各种可能组合至少出现一次,这样一来,直接对判定式进行测试就OK,因此,理解什么是单元测试很重要,并不是说什么代码都需要去测试,那样只会徒劳