题目
小凸和小方相约玩密室逃脱,这个密室是一棵有n个节点的完全二叉树,每个节点有一个灯泡。点亮所有灯
泡即可逃出密室。每个灯泡有个权值Ai,每条边也有个权值bi。点亮第1个灯泡不需要花费,之后每点亮4
个新的灯泡V的花费,等于上一个被点亮的灯泡U到这个点V的距离Du,v,乘以这个点的权值Av。在点灯
的过程中,要保证任意时刻所有被点亮的灯泡必须连通,在点亮一个灯泡后必须先点亮其子树所有灯泡才能点亮其他灯泡。请告诉他们,逃出密室的最少花费是多少。
输入格式
第1行包含1个数n,代表节点的个数
第2行包含n个数,代表每个节点的权值ai。(i=l,2,…,n)
第3行包含n-l个数,代表每条边的权值bi,第i号边是由第(i+1)/2号点连向第i+l号点的边。
(i=l,2...N-1)
输出格式
输出包含1个数,代表最少的花费。
输入样例
3
5 1 2
2 1
输出样例
5
提示
对于100%的数据,1≤N≤2×105,1<Ai,Bi≤10^5
题解
首先,此题有一些比较重要的性质:
①这棵树是一棵完全二叉树
②每次要处理完一个子树才能往祖先节点处理
③所有时刻点亮的点必须联通
④初始可以从任意点开始点亮
由这些性质,我们会发现从一个节点出发,整棵树被点亮的顺序是比较固定的,
点亮一个点u,然后点亮其子树
然后再点亮u的父亲,然后点亮u的兄弟的子树
然后点亮u父亲的父亲,点亮u父亲的父亲的兄弟的子树
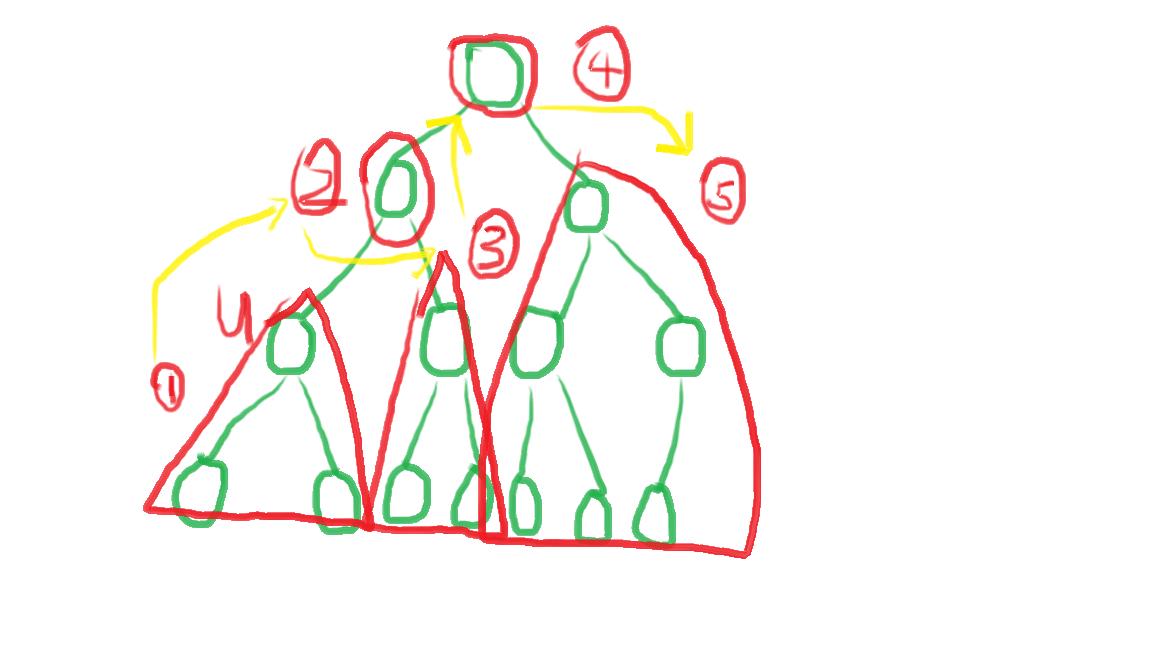
像这样
设\\(g[i][j]\\)表示从\\(i\\)节点开始,点亮\\(i\\)所在子树,然后点亮\\(i\\)位于第\\(j\\)层的祖先的最小费用
如果我们知道\\(g[i][j]\\),就可以枚举出发点,然后模拟上图的过程算出最后的代价
现在问题转化为如何求\\(g[i][j]\\)
考虑树形dp的模式
对于节点u,我们想要求出\\(g[u][j]\\)
①u为叶子节点,直接计算到\\(j\\)层祖先的价值,如果该祖先为v,则\\(g[u][j] = (d[u] - d[v])*a[v]\\)【d[u]指到根距离】
②u只有一个儿子,记为s,当然是\\(g[u][j] = b[s] * a[s] + g[s][j]\\)
③u有两个儿子
此时有两种选择:
1°先走左子树,然后走到右子树,再走到\\(j\\)层的父亲
2°先走右子树,然后走到左子树,再走到\\(j\\)层的父亲
对于两种选择,我们求出最小者
诶?等等,走到父亲的花费就是\\(g\\),但走到兄弟的花费呢?
我们记\\(f[i][j]\\)表示从节点\\(i\\)访问其子树并走到第\\(j\\)层的兄弟的最小花费
那么这两种选择就可以写成:
\\(min(b[ls] * a[ls] + f[ls][dep[rs]] + g[rs][j],
b[rs] * a[rs] + f[rs][dep[ls]] + g[ls][j])\\)
现在问题就转化成了求\\(f[i][j]\\)
用同样的思想,我们对节点u有:
①如果u为叶子节点,可以直接求出其\\(f[i][j] = dis * a[v]\\)
②如果u只有一个儿子,记为s,\\(f[i][j] = b[s] * a[s] + f[s][j]\\)
③u有两个儿子,
同样有两种类似的选择
\\(min(b[ls] * a[ls] + f[ls][dep[rs]] + f[rs][j],
b[rs] * a[rs] + f[rs][dep[ls]] + f[ls][j])\\)
那么这样,这题我们就做完啦
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u]; k; k = ed[k].nxt)
using namespace std;
const int maxn = 200005,maxm = 100005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57) {if (c == \'-\') flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = (out << 1) + (out << 3) + c - \'0\'; c = getchar();}
return out * flag;
}
LL g[maxn][20],f[maxn][20];
LL n,a[maxn],b[maxn],d[maxn],dep[maxn];
void cal(){
for (int i = n; i; i--){
int ls = i << 1,rs = i << 1 | 1;
for (int j = dep[i]; j; j--){
int s = (i >> (dep[i] - j)) ^ 1,fa = s >> 1;
if (ls > n) f[i][j] = (d[i] - d[fa] + b[s]) * a[s];
else if (rs > n) f[i][j] = a[ls] * b[ls] + f[ls][j];
else f[i][j] = min(
a[ls] * b[ls] + f[ls][dep[ls]] + f[rs][j],
a[rs] * b[rs] + f[rs][dep[rs]] + f[ls][j]
);
}
}
for (int i = n; i; i--){
int ls = i << 1,rs = i << 1 | 1;
if (ls > n) g[i][0] = 0;
else if (rs > n) g[i][0] = a[ls] * b[ls] + g[ls][0];
else g[i][0] = min(
a[ls] * b[ls] + f[ls][dep[ls]] + g[rs][0],
a[rs] * b[rs] + f[rs][dep[rs]] + g[ls][0]
);
for (int j = dep[i] - 1; j; j--){
int fa = (i >> (dep[i] - j));
if (ls > n) g[i][j] = (d[i] - d[fa]) * a[fa];
else if (rs > n) g[i][j] = a[ls] * b[ls] + g[ls][j];
else g[i][j] = min(
a[ls] * b[ls] + f[ls][dep[ls]] + g[rs][j],
a[rs] * b[rs] + f[rs][dep[rs]] + g[ls][j]
);
}
}
}
void solve(){
LL ans = g[1][0];
for (int i = 2; i <= n; i++){
LL cost = g[i][dep[i] - 1];
int x,fa;
for (int u = i; u > 1; u >>= 1){
x = u ^ 1; fa = u >> 1;
if (x > n) cost += b[fa] * a[fa >> 1];
else cost += a[x] * b[x] + g[x][dep[fa] - 1];
}
ans = min(ans,cost);
}
printf("%lld\\n",ans);
}
int main(){
n = read();
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 2; i <= n; i++) b[i] = read();
dep[1] = 1;
for (int i = 1; i <= n; i++){
if ((i << 1) <= n){
dep[i << 1] = dep[i] + 1;
d[i << 1] = d[i] + b[i << 1];
}
if ((i << 1 | 1) <= n){
dep[i << 1 | 1] = dep[i] + 1;
d[i << 1 | 1] = d[i] + b[i << 1 | 1];
}
}
cal();
solve();
return 0;
}