倍道而行：二分搜索树的遍历前中后序遍历（深度优先遍历）+层序遍历广度优先遍历

Posted 2020-10-27 yuhui-snail

先看下前中后序遍历的顺序是怎么样的：

---

下面通过一个例子来具体的描述前序遍历的流程：

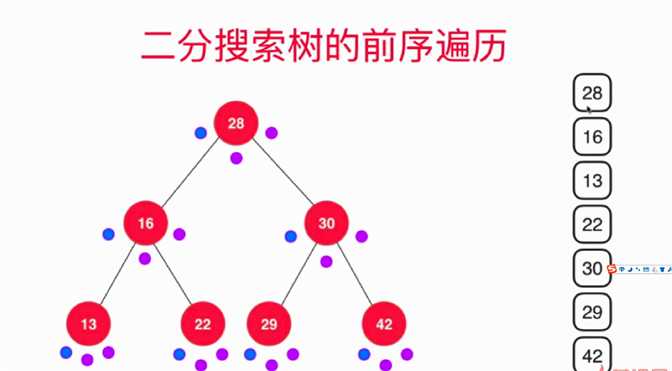
以下都以“节点”代替，比如：“28”指的是 “28这个节点”。

流程顺序是：自、左、右

• 1.先访问“28”，然后访问“28”左节点即“16”。
• 2.然后“16”的左节点即“13”。好，这里是关键，“13”没继续访问其左节点，发现没有左节点，然后就访问自己，然后再访问其右节点。
• 3.开始回溯，访问“16”，再访问“16”的右节点“22”，“22”的左右都没有，回到“16”，再到“28”，在访问“28”的左节点
• 4.继续以上流程。

 下面画个图来表示顺序：

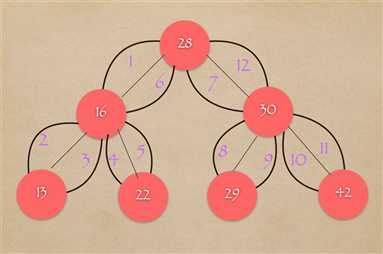
下面是代码实现：

 // 对以node为根的二叉搜索树进行前序遍历
    void preOrder(Node* node){

        if( node != NULL ){
            cout<<node->key<<endl;
            preOrder(node->left);
            preOrder(node->right);
        }
    }

---

  这属于深度遍历的方法，一下走到最下面“13”节点。

下面给出中序和后续的代码：

 // 对以node为根的二叉搜索树进行中序遍历
    void inOrder(Node* node){

        if( node != NULL ){
            inOrder(node->left);
            cout<<node->key<<endl;
            inOrder(node->right);
        }
    }

    // 对以node为根的二叉搜索树进行后序遍历
    void postOrder(Node* node){

        if( node != NULL ){
            postOrder(node->left);
            postOrder(node->right);
            cout<<node->key<<endl;
        }
    }

 

代码的是不是很像，但是打印的顺序是不一样的。 

---

 

层序遍历【广度优先遍历】 ：

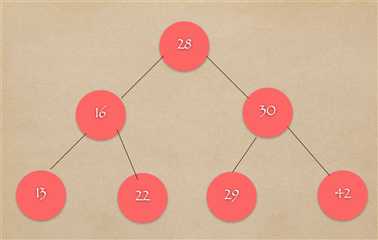
层序遍历就是：一层层的来，从28-16-30-13-22-29-42，这样的顺序。

这里需要用到队列，如图：

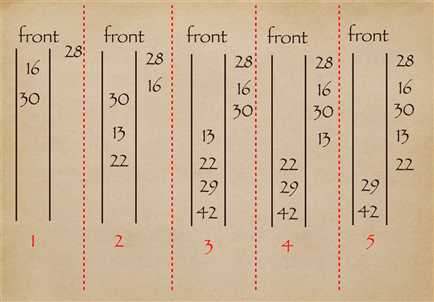
大致流程：

• 28入队，然后出队【就是进行处理】然后起左右两节点入队，即16和30.
• 然后16出队【进行处理】，然后16的左右子节点入队，即13和22.
• 然后30出队【进行处理】，然后30的左右子节点入队，即29和42.
• 然后在13出队【进行处理】，然后13的左右子节点入队，但是木有
• 继续22出队【进行处理】，然后22的左右子节点入队，但是木有
• ......

代码：

 // 层序遍历
    void levelOrder(){

        queue<Node*> q;
        q.push(root);
        while( !q.empty() ){

            Node *node = q.front();
            q.pop();

            cout<<node->key<<endl;

            if( node->left )
                q.push( node->left );
            if( node->right )
                q.push( node->right );
        }
    }