题目背景
byx和手气君都非常都非常喜欢种树。有一天,他们得到了两颗奇怪的树种,于是各自取了一颗回家种树,并约定几年后比一比谁种出来的树更加牛x。
题目描述
很快,这棵树就开花结果了。byx和手气君惊讶的发现,这是一棵主席树,树上长满了主席和主席的朋友们。这棵树上一共有五种人,主席(J),记者(HK),高人(W),女王(E)和膜法师(YYY)。他们发现,他们的主席树上的人数相同,都为N。
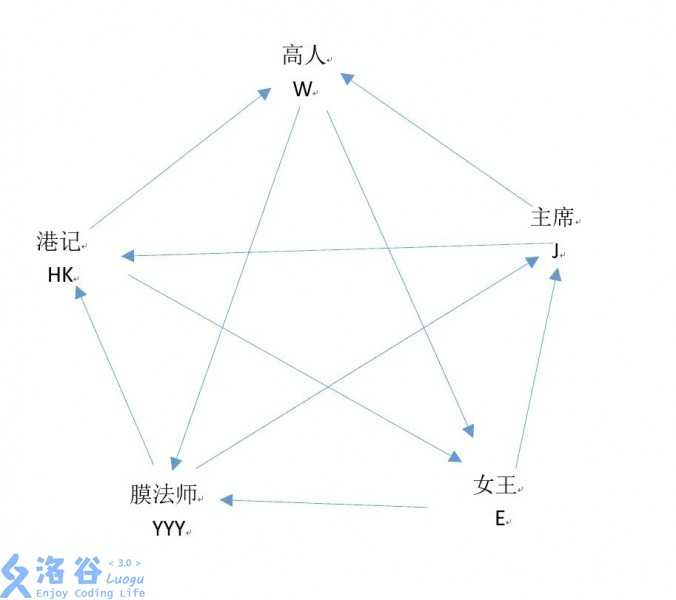
研究发现,这五种人的输赢如上图所示(一样的人不能PK),箭头指向输的人。至于为什么,留给同学们自己思考。
比赛如期进行。
byx和手气君要进行M场比赛,每一场比赛他们会选出树上的两个人来比较看谁更牛x。
第i个人寿命为Lifei秒,每次比完赛他们就会-1s。当他们生命为0s时他们就不能再比赛了。
同时,当J的寿命为0时,同一棵树上的YYY可以为他+1s。每个YYY只能给.每个J续一次。
那么问题来了
现在给定N,M(1≤N≤100,1≤M≤1000),A和B每一个人所属种类(J,HK,W,YYY或E)以及每一个人的生命,生命不超过50.请你算算A最多能够赢得多少场比赛呢。
数据保证每一场一定都有人用。两个人之间只能比一场。
输入输出格式
输入格式:
第一行包含两个数N,M,含义看上面。
第二行N个字串(J,HK,W,YYY或E),表示byx的人所属种类,用空格隔开。
第三行N个字串(J,HK,W,YYY或E),表示手气君的人所属种类,用空格隔开。
第四行N个数,表示byx的人的生命。
第五行N个数,表示手气君的人的生命。
输出格式:
一个数,byx能赢的场次
输入输出样例
输入样例#1: 复制
3 3
J W YYY
J HK E
2 2 2
2 2 2
输出样例#1: 复制
3
说明
第一场主席赢记者,第二场高人赢女王,第三场膜法师赢记者
题解:源点向每个人建容量为hp的边,如果是长者,则容量增加魔法师条.每个人向另一组中克制的人建容量为一的边,另一组每个人向汇点建容量为hp的边,然后跑一遍dinic就搞定了
代码如下:
#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define inf 0x3f3f3f3f using namespace std; int head[100010],next[100010],w[100010],v[100010],deep[100010],cur[100010]; int s,t,cnt; void init() { cnt=-1; memset(head,-1,sizeof(head)); memset(next,-1,sizeof(next)); } void add(int from,int to,int cost) { cnt++; next[cnt]=head[from]; w[cnt]=cost; v[cnt]=to; head[from]=cnt; } void add_edge(int from,int to,int cost) { add(from,to,cost); add(to,from,0); } int bfs(int s,int t) { queue<int> q; memset(deep,0,sizeof(deep)); deep[s]=1; q.push(s); while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u]; i!=-1; i=next[i]) { if(!deep[v[i]]&&w[i]) { deep[v[i]]=deep[u]+1; q.push(v[i]); } } } if(!deep[t]) { return 0; } return 1; } int dfs(int u,int t,int dist) { if(u==t) { return dist; } for(int i=head[u]; i!=-1; i=next[i]) { if(w[i]&&deep[v[i]]==deep[u]+1) { int di=dfs(v[i],t,min(dist,w[i])); if(di>0) { w[i]-=di; w[i^1]+=di; return di; } } } return 0; } int dinic(int s,int t) { int ans=0; while(bfs(s,t)) { while(int d=dfs(s,t,inf)) { ans+=d; } } return ans; } int main() { int n,m,kd1[110],kd2[110],hp1[110],hp2[110],cnt1=0,cnt2=0; char s1[20]; init(); scanf("%d%d",&n,&m); s=0;t=2*n+1; for(int i=1;i<=n;i++) { cin>>s1; if(s1[0]==‘W‘) { kd1[i]=1; } if(s1[0]==‘J‘) { kd1[i]=2; } if(s1[0]==‘E‘) { kd1[i]=3; } if(s1[0]==‘Y‘) { kd1[i]=4; cnt1++; } if(s1[0]==‘H‘) { kd1[i]=5; } } for(int i=1;i<=n;i++) { cin>>s1; if(s1[0]==‘W‘) { kd2[i]=1; } if(s1[0]==‘J‘) { kd2[i]=2; } if(s1[0]==‘E‘) { kd2[i]=3; } if(s1[0]==‘Y‘) { kd2[i]=4; cnt2++; } if(s1[0]==‘H‘) { kd2[i]=5; } } for(int i=1;i<=n;i++) { cin>>hp1[i]; } for(int i=1;i<=n;i++) { cin>>hp2[i]; } for(int i=1;i<=n;i++) { add_edge(s,i,hp1[i]); add_edge(i+n,t,hp2[i]); if(kd1[i]==2) { add_edge(s,i,cnt1); } if(kd2[i]==2) { add_edge(i+n,t,cnt2); } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(kd1[i]==1) { if(kd2[j]==3||kd2[j]==4) { add_edge(i,j+n,1); } } if(kd1[i]==2) { if(kd2[j]==1||kd2[j]==5) { add_edge(i,j+n,1); } } if(kd1[i]==3) { if(kd2[j]==2||kd2[j]==4) { add_edge(i,j+n,1); } } if(kd1[i]==4) { if(kd2[j]==2||kd2[j]==5) { add_edge(i,j+n,1); } } if(kd1[i]==5) { if(kd2[j]==1||kd2[j]==3) { add_edge(i,j+n,1); } } } } int ans=min(dinic(s,t),m); printf("%d\\n",ans); }
评级竟然是NOI/NOI+/CTSC?emmm....