---恢复内容开始---
一、仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 。有理数基本运算:
1、构造有理数T,元素e1,e2分别被赋以分子、分母值
2、销毁有理数T
3、用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4、将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5、有理数T1,T2相加,结果存入有理数T3
6、有理数T1,T2相减,结果存入有理数T3
7、有理数T1,T2相乘,结果存入有理数T3
8、有理数T1,T2相除,结果存入有理数T3二.内容。
1.抽象数据类型
ADT Rational{
数据对象:
D={e1,e2|e1,e2均为整数}
数据关系:
R={<e1,e2>|e1是分子,e2是分母且不为0};
基础运算:
gouzhao(&e,e1,e2)//构造有理数;
void jia(int e1,int e2,int e3,int e4);//加法
void jian(int e1,int e2,int e3,int e4);//减法
void cheng(int e1,int e2,int e3,int e4);//乘法
void chu(int e1,int e2,int e3,int e4);//除法
int simply(int a,int b);//判断公约数三。数据结构及函数
1.头文件
2.函数
加法
减法
除法
乘法
求最大公约数
四。结果展示
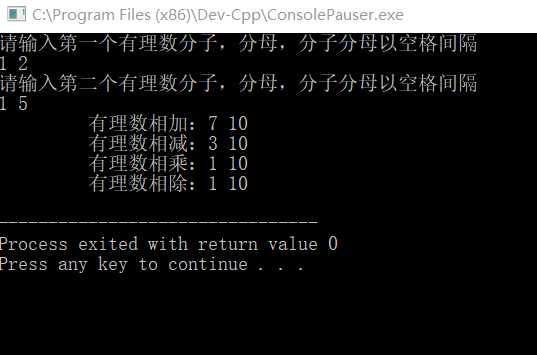
1.正数
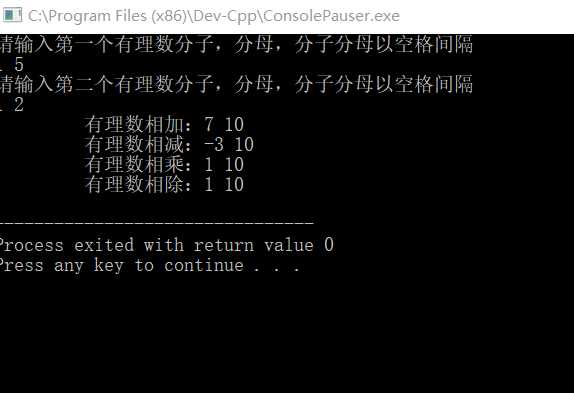
2.负数
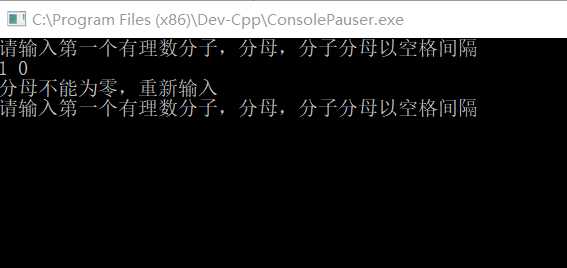
3.无意义
五。总结
数据结构是编程的核心和基础,由基本的数据类型构成并包括相关的操作,提高了算法的效率,有点类似数据的集合,也代表了多个数据间的关系
---恢复内容结束---