Deep Learning学习 之 卷积神经网络（文字识别系统LeNet-5）

Posted 2020-07-07 SuPhoebe

部分预备知识可以先看博文，统一了一些专业名词。

原文摘自，在此文中对原文增加了一些注释和修改，统一了与之前博文的专业名词说法，有助于理解。

！！！如果读者发现一些数学符号后面有一些奇怪的竖线，那是CSDN的Latex除了问题，大家自行过滤。

在经典的模式识别中，一般是事先提取特征。提取诸多特征后，要对这些特征进行相关性分析，找到最能代表字符的特征，去掉对分类无关和自相关的特征。然而，这些特征的提取太过依赖人的经验和主观意识，提取到的特征的不同对分类性能影响很大，甚至提取的特征的顺序也会影响最后的分类性能。同时，图像预处理的好坏也会影响到提取的特征。那么，如何把特征提取这一过程作为一个自适应、自学习的过程，通过机器学习找到分类性能最优的特征呢？那就是采用卷积神经网络。

卷积神经元每一个隐层的单元提取上一层图像的局部特征，将其映射成一个平面，特征映射函数采用 sigmoid 函数作为卷积网络的激活函数，使得特征映射具有位移不变性。每个神经元与前一层的局部感受野相连。注意前面我们说了，不是局部连接的神经元权值相同，而是同一平面层的神经元权值共享，有相同程度的位移、旋转不变性。每个特征提取后都紧跟着一个用来求局部平均与二次提取的亚取样层（或下采样层，subsampling layers的翻译很多种多样）。这种特有的两次特征提取结构使得网络对输入样本有较高的畸变容忍能力。也就是说，卷积神经网络通过局部感受野、共享权值和亚取样来保证图像对位移、缩放、扭曲的鲁棒性。

文字识别系统LeNet-5

一种典型的用来识别数字的卷积网络是LeNet-5(paper和效果)。当年美国大多数银行就是用它来识别支票上面的手写数字的。能够达到这种商用的地步，它的准确性可想而知。毕竟目前学术界和工业界的结合是最受争议的。

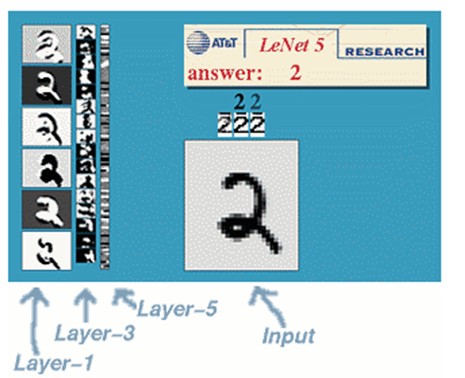
卷积网络结构说明

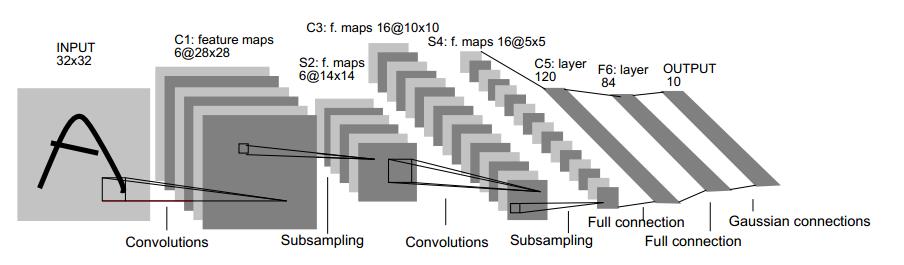
LeNet-5共有7层，不包含输入，每层都包含可训练参数（连接权重）。输入图像为$32\\times 32$大小。这要比Mnist数据库（一个公认的手写数据库，大小应该是$28\\times 28$）中最大的字母还大。这样做的原因是希望潜在的明显特征如笔画断电或角点能够出现在最高层特征监测子感受野的中心。

首先，简要解释下上面这个用于文字识别的LeNet-5深层卷积网络：

1. 输入图像是$32\\times 32$的大小，过滤器的大小是$5\\times 5$的，由于不考虑对图像的边界进行拓展（narrow CNN），则过滤器将有$28\\times 28$（32 - 5 + 1 = 28，其中1是步长）个不同的位置，也就是C1面的大小是28x28。这里设定C1层中有6个不同的C1面，每一个C1面内的权值是共享的。

2. S2层是一个下采样层（subsampling layer）。简单的说，由4个点下采样为1个点，也就是4个数的加权平均。但在LeNet-5系统，下采样层比较复杂，因为这4个加权系数也需要学习得到，这显然增加了模型的复杂度。在斯坦福关于深度学习的教程中，这个过程叫做Pool。S2面的大小是$14\\times 14$，其中$14 = {28\\over 2}$。

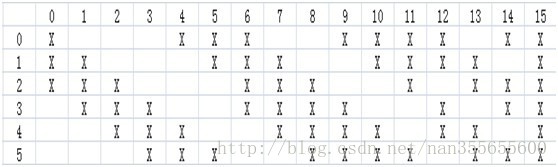
3. 根据对前面C1层同样的理解，我们很容易得到C3面的大小为$10\\times10$（大家可以自己想一想怎么算的，下文再给答案）。 只不过，C3层的变成了16个$10\\times 10$网络! （我猜测，之前的6个面，这里16个面都是通过测试选择的比较优秀的参数）试想一下，如果S2层只有1个平面，那么由S2层得到C3就和由输入层得到C1层是完全一样的。但是，S2层由多层，那么，我们只需要按照一定的顺利组合这些层就可以了。具体的组合规则，在 LeNet-5 系统中给出了下面的表格：
   

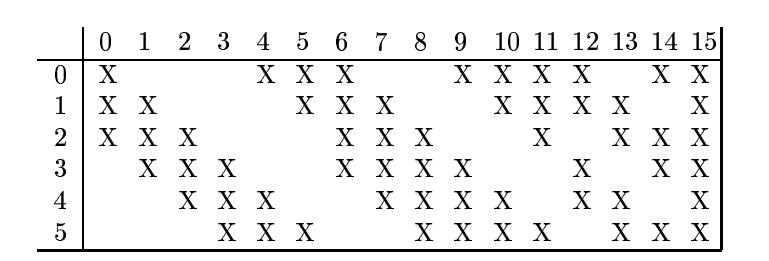
简单的说，例如对于C3层的第0张特征图（第0张C3面），其每一个节点与S2层的第0张特征图，第1张特征图，第2张特征图，总共3个$5\\times 5$个节点相连接。后面依次类推，C3层每一张特征映射图的权值是相同的。

4.S4 层是在C3层基础上下采样，前面已述。在后面的层由于每一层节点个数比较少，都是全连接层，这个比较简单，不再赘述。

C3面的边长：$14-5+1=10$，其中14是上一层的边长，5是过滤器边长，1是步长。

涉及问题

1、每个图如何卷积：

（1）一个图如何变成几个？

（2）卷积核如何选择？

2、节点之间如何连接？

3、S2-C3如何进行分配？

4、16-120全连接如何连接？

5、最后output输出什么形式？

①各个层解释：

我们先要明确一点：每个层有多个Feature Map，每个Feature Map通过一种卷积滤波器提取输入的一种特征，然后每个Feature Map有多个神经元。

(1) C1层是一个卷积层（为什么是卷积？卷积运算一个重要的特点就是，通过卷积运算，可以使原信号特征增强，并且降低噪音），由6个特征图Feature Map构成。特征图中每个神经元与输入中$5\\times 5$的邻域相连。特征图的大小为28*28，这样能防止输入的连接掉到边界之外（是为了BP反馈时的计算，不致梯度损失，个人见解）。C1有156个可训练参数（每个滤波器$5\\times 5=25$个unit参数和一个bias参数，一共6个滤波器，共$(5\\times 5+1)\\times 6=156$个参数），共$156\\times (28\\times 28)=122,304$个连接。（连接的计算：连接数 = 所有神经元可训练的权值数 = 每个神经元节点有多少个可以训练的权值 $\\times$神经元个数）

(2) S2层是一个下采样层（为什么是下采样？利用图像局部相关性的原理，对图像进行子抽样，可以减少数据处理量同时保留有用信息），有6个$14\\times 14$的特征图。特征图中的每个单元与C1中相对应特征图的$2\\times 2$邻域相连接（至于为什么是$2\\times 2$的，是人为设计的，可以是一个结合运算时间和运算结果平衡点，设计得太小了导致运算结果误差大，设计太大了导致运算时间过长）。S2层每个单元的4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid函数计算。可训练系数和偏置控制着sigmoid函数的非线性程度。如果系数比较小，那么运算近似于线性运算，亚采样相当于模糊图像。如果系数比较大，根据偏置的大小亚采样可以被看成是有噪声的“或”运算或者有噪声的“与”运算。每个单元的2*2感受野并不重叠，因此S2中每个特征图的大小是C1中特征图大小的1/4（行和列各1/2）。S2层有$6\\times (1+1) = 12$个可训练参数（由于权值共享，每个面只有2个参数需要训练）和5880个连接。（我不懂这个$5880( = 14 \\times 14 \\times 30)$是怎么算出来的，如果各位读者有人知道，请在底下评论，不甚感激）

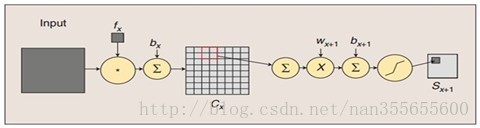
图：卷积和子采样过程.

卷积过程：用一个可训练的滤波器fx去卷积一个输入的图像（第一阶段是输入的图像，后面的阶段就是卷积特征map了），然后加一个偏置bx，得到卷积层Cx。

子采样过程：每邻域四个像素求和变为一个像素，然后通过标量$W_{x+1}$加权，再增加偏置$b_{x+1}$，然后通过一个sigmoid激活函数，产生一个大概缩小四倍的特征映射图$S_{x+1}$。（这个角标是我自己加的，我不知道原文中Wx+1的那个+1到底是加数值还是加角标，不过看代码来说，感觉加角标更可能）

所以从一个平面到下一个平面的映射可以看作是作卷积运算，S-层可看作是模糊滤波器，起到二次特征提取的作用。隐层与隐层之间空间分辨率递减，而每层所含的平面数递增，这样可用于检测更多的特征信息。

(3) C3层也是一个卷积层，它同样通过5x5的卷积核去卷积层S2，然后得到的特征map就只有10x10个神经元，但是它有16种不同的卷积核，所以就存在16个特征map了。这里需要注意的一点是：C3中的每个特征map是连接到S2中的所有6个或者几个特征map的，表示本层的特征map是上一层提取到的特征map的不同组合（这个做法也并不是唯一的，只要保证足够的非对称性。这里用到的是组合，就像之前聊到的人的视觉系统一样，底层的结构构成上层更抽象的结构，例如边缘构成形状或者目标的部分）。

刚才说C3中每个特征图由S2中所有6个或者几个特征map组合而成。为什么不把S2中的每个特征图连接到每个C3的特征图呢？原因有2点。第一，不完全的连接机制将连接的数量保持在合理的范围内。第二，也是最重要的，其破坏了网络的对称性。由于不同的特征图有不同的输入，所以迫使他们抽取不同的特征（我们希望提取出的特征是互补的)。

例如，存在的一个方式是：C3的前6个特征图以S2中3个相邻的特征图子集为输入，接下来6个特征图以S2中4个相邻特征图子集为输入，然后的3个以不相邻的4个特征图子集为输入，最后一个将S2中所有特征图为输入。这样C3层有1516个可训练参数和151600个连接。

(4) S4层是一个下采样层，由16个$5\\times 5$大小的特征图构成。特征图中的每个单元与C3中相应特征图的2*2邻域相连接，跟C1和S2之间的连接一样。S4层有32个可训练参数（每个特征图1个因子和一个偏置）和2000个连接。

(5) C5层是一个卷积层，有120个特征图。每个单元与S4层的全部16个单元的5*5邻域相连。由于S4层特征图的大小也为5*5（同过滤器大小一样），故C5特征图的大小为1*1：这构成了S4和C5之间的全连接。之所以仍将C5标示为卷积层而非全相联层，是因为如果LeNet-5的输入变大，而其他的保持不变，那么此时特征图的维数就会比1*1大。C5层有48120个可训练连接。

(6) F6层有84个单元（之所以选这个数字的原因来自于输出层的设计），与C5层全相连。有10164个可训练参数。如同经典神经网络，F6层计算输入向量和权重向量之间的点积，再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。

(7) 最后，输出层由欧式径向基函数（Euclidean Radial Basis Function）单元组成，每类一个单元，每个有84个输入。换句话说，每个输出RBF单元计算输入向量和参数向量之间的欧式距离。输入离参数向量越远，RBF输出的越大。一个RBF输出可以被理解为衡量输入模式和与RBF相关联类的一个模型的匹配程度的惩罚项。

用概率术语来说，RBF输出可以被理解为F6层配置空间的高斯分布的负log-likelihood。给定一个输入模式，损失函数应能使得F6的配置与RBF参数向量（即模式的期望分类）足够接近。这些单元的参数是人工选取并保持固定的（至少初始时候如此）。这些参数向量的成分被设为-1或1。虽然这些参数可以以-1和1等概率的方式任选，或者构成一个纠错码，但是被设计成一个相应字符类的7*12大小（即84）的格式化图片。这种表示对识别单独的数字不是很有用，但是对识别可打印ASCII集中的字符串很有用。

用这种分布编码而非更常用的“1 of N”编码用于产生输出的另一个原因是，当类别比较大的时候，非分布编码的效果比较差。原因是大多数时间非分布编码的输出必须为0。这使得用sigmoid单元很难实现。另一个原因是分类器不仅用于识别字母，也用于拒绝非字母。使用分布编码的RBF更适合该目标。因为与sigmoid不同，他们在输入空间的较好限制的区域内兴奋，而非典型模式更容易落到外边。

RBF参数向量起着F6层目标向量的角色。需要指出这些向量的成分是+1或-1，这正好在F6 sigmoid的范围内，因此可以防止sigmoid函数饱和。实际上，+1和-1是sigmoid函数的最大弯曲的点处。这使得F6单元运行在最大非线性范围内。必须避免sigmoid函数的饱和，因为这将会导致损失函数较慢的收敛和病态问题。

②问题讲解

第一个问题

（1）输入$\\rightarrow$C1

用6个5*5大小的patch（即权值，训练得到，随机初始化，在训练过程中调节）对32*32图片进行卷积，得到6个特征图。

（2）S2$\\rightarrow$C3

C3那16张10*10大小的特征图是怎么来？

将S2的特征图用1个输入层为150（=5*5*6，不是5*5）个节点，输出层为16个节点的网络进行convolution。

该第3号特征图的值（假设为H3）是怎么得到的呢？

首先，我们把网络150-16（以后这样表示，表面输入层节点为150，隐含层节点为16）中输入的150个节点分成6个部分，每个部分为连续的25个节点。

根据图中规则，取出倒数第3个部分的节点（为25个），且同时是与隐含层16个节点中的第4（因为对应的是3号，从0开始计数的）个相连的那25个值，reshape为5*5大小，用这个5*5大小的特征patch去卷积S2网络中的倒数第3个特征图，假设得到的结果特征图为h1。

同理，取出网络150-16中输入的倒数第2个部分的节点（为25个），且同时是与隐含层16个节点中的第5个相连的那25个值，reshape为5*5大小，用这个5*5大小的特征patch去convolution S2网络中的倒数第2个特征图，假设得到的结果特征图为h2。

最后，取出网络150-16中输入的最后1个部分的节点（为25个），且同时是与隐含层16个节点中的第5个相连的那25个值，reshape为5*5大小，用这个5*5大小的特征patch去convolution S2网络中的最后1个特征图，假设得到的结果特征图为h3。

最后将h1，h2，h3这3个矩阵相加得到新矩阵h，并且对h中每个元素加上一个偏移量b，且通过sigmoid的激发函数，即可得到我们要的特征图H3了。

第二个问题

上图S2中为什么是150个节点？（涉及到权值共享和参数减少）

CNN一个牛逼的地方就在于通过感受野和权值共享减少了神经网络需要训练的参数的个数。

下图左：如果我们有1000x1000像素的图像，有1百万个隐层神经元，那么他们全连接的话（每个隐层神经元都连接图像的每一个像素点），就有1000x1000x1000000=10^12个连接，也就是10^12个权值参数。然而图像的空间联系是局部的，就像人是通过一个局部的感受野去感受外界图像一样，每一个神经元都不需要对全局图像做感受，每个神经元只感受局部的图像区域，然后在更高层，将这些感受不同局部的神经元综合起来就可以得到全局的信息了。这样，我们就可以减少连接的数目，也就是减少神经网络需要训练的权值参数的个数了。如下图右：假如局部感受野是10x10，隐层每个感受野只需要和这10x10的局部图像相连接，所以1百万个隐层神经元就只有一亿个连接，即10^8个参数。比原来减少了四个0（数量级），这样训练起来就没那么费力了，但还是感觉很多的啊，那还有啥办法没？

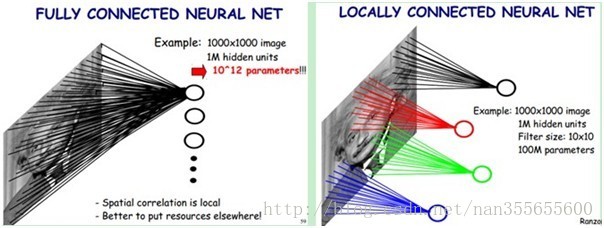
我们知道，隐含层的每一个神经元都连接10x10个图像区域，也就是说每一个神经元存在10x10=100个连接权值参数。那如果我们每个神经元这100个参数是相同的呢？也就是说每个神经元用的是同一个卷积核去卷积图像。这样我们就只有多少个参数？？只有100个参数啊！！！亲！不管你隐层的神经元个数有多少，两层间的连接我只有100个参数啊！亲！这就是权值共享啊！亲！这就是卷积神经网络的主打卖点啊！亲！（有点烦了，呵呵）也许你会问，这样做靠谱吗？为什么可行呢？这个……共同学习。

好了，你就会想，这样提取特征也忒不靠谱吧，这样你只提取了一种特征啊？对了，真聪明，我们需要提取多种特征对不？假如一种滤波器，也就是一种卷积核就是提出图像的一种特征，例如某个方向的边缘。那么我们需要提取不同的特征，怎么办，加多几种滤波器不就行了吗？对了。所以假设我们加到100种滤波器，每种滤波器的参数不一样，表示它提出输入图像的不同特征，例如不同的边缘。这样每种滤波器去卷积图像就得到对图像的不同特征的放映，我们称之为Feature Map。所以100种卷积核就有100个Feature Map。这100个Feature Map就组成了一层神经元。到这个时候明了了吧。我们这一层有多少个参数了？100种卷积核x每种卷积核共享100个参数=100x100=10K，也就是1万个参数。才1万个参数啊！亲！（又来了，受不了了！）见下图右：不同的颜色表达不同的滤波器。

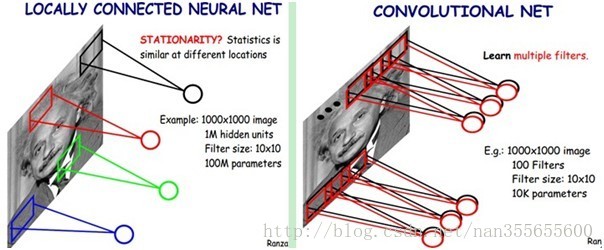
嘿哟，遗漏一个问题了。刚才说隐层的参数个数和隐层的神经元个数无关，只和滤波器的大小和滤波器种类的多少有关。那么隐层的神经元个数怎么确定呢？它和原图像，也就是输入的大小（神经元个数）、滤波器的大小和滤波器在图像中的滑动步长都有关！例如，我的图像是1000x1000像素，而滤波器大小是10x10，假设滤波器没有重叠，也就是步长为10，这样隐层的神经元个数就是(1000x1000 )/ (10x10)=100x100个神经元了，假设步长是8，也就是卷积核会重叠两个像素，那么……我就不算了，思想懂了就好。注意了，这只是一种滤波器，也就是一个Feature Map的神经元个数哦，如果100个Feature Map就是100倍了。由此可见，图像越大，神经元个数和需要训练的权值参数个数的贫富差距就越大。

所以这里可以知道刚刚14*14的图像计算它的节点，按步长为3计算，则一幅图可得5*5个神经元个数，乘以6得到150个神经元个数。

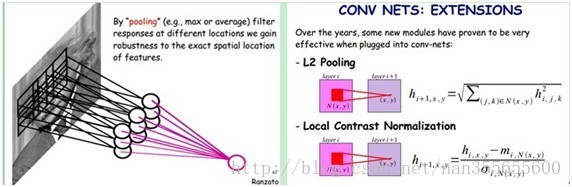
需要注意的一点是，上面的讨论都没有考虑每个神经元的偏置部分。所以权值个数需要加1 。这个也是同一种滤波器共享的。

总之，卷积网络的核心思想是将：局部感受野、权值共享（或者权值复制）以及时间或空间亚采样这三种结构思想结合起来获得了某种程度的位移、尺度、形变不变性。

第三个问题：

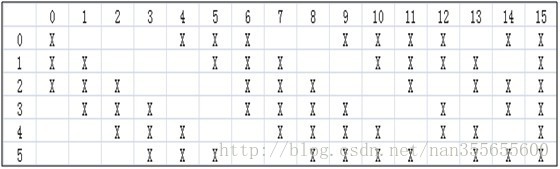
如果C1层减少为4个特征图，同样的S2也减少为4个特征图，与之对应的C3和S4减少为11个特征图，则C3和S2连接情况如图：

大家仔细观察一下这些图，就能够发现规律，这些图的设计并不是需要严格推导设计的，而是按照一定规律设计就行（如果是完全随机的，可能效果并不如按照规律设计的好），所有规则都可能是通过测试最终结果修改得到的。

第四个问题：

全连接：

C5对C4层进行卷积操作，采用全连接方式，即每个C5中的卷积核均在S4所有16个特征图上进行卷积操作。

第五个问题：

采用one-of-c的方式，在输出结果的1*10的向量中最大分量对应位置极为网络输出的分类结果。对于训练集的标签也采用同样的方式编码，例如1000000000，则表明是数字0的分类。

简化的LeNet-5系统

简化的LeNet-5系统把下采样层和卷积层结合起来，避免了下采样层过多的参数学习过程，同样保留了对图像位移，扭曲的鲁棒性。其网络结构图如下所示：

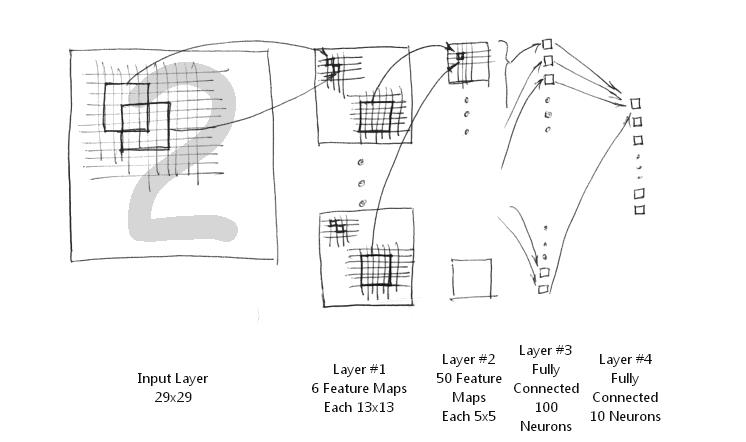
简化的LeNet-5系统包括输入层的话，只有5层结构，而原始LeNet-5结构不包含输入层就已经是7层网络结构了。它实现下采样非常简单，直接取其第一个位置节点上的值可以了。

1、 输入层。MNIST手写数字图像的大小是$28\\times 28$的，这里通过补零扩展为29x29的大小（wide CNN）。这样输入层神经节点个数为29x29等于841个。

2、第一层。由6张不同的特征映射图组成。每一张特征图的大小是13x13。（其中$13\\times 2+5-2=29，2是步长$） 注意，由于卷积窗大小为5x5，加上下采样过程，易得其大小为13x13. 所以, 第二层共有6x13x13等于1014个神经元节点。每一张特征图加上偏置共有5x5+1等于26个权值需要训练，总共有6x26等于156个不同的权值。即总共有1014x156等于26364条连接线。

3、 第二层。由50张不同的特征映射图组成。每一张特征图的大小是5x5. 注意，由于卷积窗大小为5x5，加上下采样过程，易得其大小为5x5. 由于上一 层是由多个特征映射图组成，那么，如何组合这些特征形成下一层特征映射图的节点呢？简化的LeNet-5系